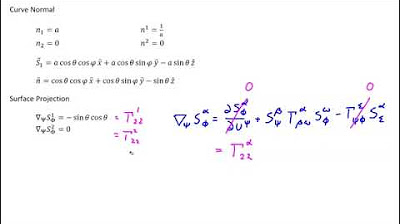Video 64 - Normal Examples
TLDRThis video script from a tensor calculus series focuses on deriving the normal components for various sample surfaces using a simplified formula. It explains the process of evaluating the normal vectors for cylindrical, spherical, and toroidal surfaces by applying the formula and utilizing a systematic technique to simplify calculations. The script also emphasizes verifying the normal vectors as unit vectors and their orthogonality to the basis vectors, providing a clear understanding of the mathematical concepts involved.
Takeaways
- 📚 The script is from a video on tensor calculus, specifically focusing on evaluating normal components for sample surfaces.
- 🔍 It introduces a derived formula for the normal, which simplifies the process of calculating the normal in any given surface.
- 📐 The formula involves the use of the epsilon tensor and the shift tensors, which are key in tensor calculus.
- 🌐 The script explains how to simplify the normal formula by considering the volume elements for both ambient and surface coordinates.
- 🔢 The normal components are calculated for each index, with the script detailing the process for the first index as an example.
- 🎯 The script uses the concept of dummy and free indices in tensor notation, highlighting permutations and their effects on the calculation.
- 📉 The process involves identifying even and odd permutations to determine the signs of the terms in the normal formula.
- 🔄 The script demonstrates how to apply the normal formula to specific coordinate systems, such as cylindrical and spherical surfaces.
- 📏 It shows that the normal vectors for these surfaces can be derived using a simplified approach based on geometric patterns.
- 📝 The script concludes with the normal components for a torus, using a substitution to simplify the calculations.
- 🧩 The takeaway is that the normal vectors for different surfaces can be systematically calculated using tensor calculus, with the script providing clear steps and examples.
Q & A
What is the main topic of this video?
-The main topic of this video is the application of a formula derived in a previous video to evaluate the normal components for various sample surfaces in tensor calculus.
What is the significance of epsilon i j k and epsilon alpha beta in the context of this video?
-Epsilon i j k and epsilon alpha beta are used to define the volume elements for the ambient and surface coordinates respectively, which are essential in expressing the formula for the normal components.
How is the normal vector formula simplified in this video?
-The normal vector formula is simplified by expressing it in terms of the square root of the volume elements and the shift tensors, which makes it more convenient for evaluating the normal in any given surface.
What technique is used to evaluate the normal vector components for each index?
-The technique involves using the permutation properties of the epsilon tensors and the shift tensors to evaluate the normal vector components for each index.
How are the dummy indices j, k, alpha, and beta handled in the formula?
-The dummy indices j, k, alpha, and beta are used in permutations to ensure that the expression is non-zero, by being different from the free index i and following the rules of even and odd permutations.
What is the significance of the shift tensors zj alpha and z k beta in the formula?
-The shift tensors zj alpha and z k beta are crucial in the calculation of the normal components as they relate the ambient coordinates to the surface coordinates.
How does the video demonstrate the evaluation of the normal vector for a cylindrical surface?
-The video demonstrates the evaluation by applying the derived formula and the components of the shift tensor specific to the cylindrical surface, leading to the normal vector components in terms of cosine and sine of theta.
What is the method to confirm that the derived normal vectors are unit vectors?
-The method involves taking the dot product of the normal vector with itself and confirming that the result is equal to one, indicating that it is a unit vector.
How does the video show that the normal vectors are orthogonal to the basis vectors of the surfaces?
-The video shows this by taking the dot product of the normal vector with the basis vectors and demonstrating that the results are zero, indicating orthogonality.
What substitution is made for the torus surface to simplify the calculation of the normal vector?
-The substitution made for the torus surface is r = a + b cosine(phi), which simplifies the expression for the square root of the surface volume element.
How does the video describe the process of deriving the normal vector for a spherical surface?
-The video describes the process by applying the simplified formula and the specific components of the shift tensor for the spherical surface, resulting in the normal vector components in terms of sine and cosine of theta and phi.
Outlines
📚 Tensor Calculus: Normal Component Evaluation
In this segment, the video script discusses the application of a formula derived in a previous video to compute the normal components for sample surfaces. The formula is simplified for convenience, drawing parallels to previous work on cross products and curl in different coordinate systems. The script unpacks the formula, explains the significance of the epsilon tensor, and demonstrates how to evaluate the normal vector for each surface by systematically working through the indexes.
🔍 Simplifying Normal Vector Computation
This paragraph delves into the simplification of the normal vector calculation process. It explains the permutation of indexes and the use of dummy indexes to avoid redundancy. The script identifies identical terms and demonstrates how to combine them, resulting in a simplified expression for the normal vector's first component. It also discusses the concept of even and odd permutations and their impact on the sign of the resulting terms.
📐 Applying the Normal Vector Model to Sample Surfaces
The script applies the derived normal vector model to specific sample surfaces, starting with a cylindrical surface. It explains how to calculate the normal vector components using the model forms and the shift tensor. The process involves evaluating the normal vector components step by step, confirming that the resulting vector is a unit vector by checking its dot product with itself and ensuring orthogonality with the basis vectors.
🌐 Spherical Surface Normal Vector Analysis
Moving on to the spherical surface, the script outlines a simplified technique for determining the normal vector components. It emphasizes the ease of computation due to the Cartesian coordinate system's properties. The script demonstrates the calculation process, resulting in the normal vector components for the spherical surface and encourages the viewer to verify that the vector is indeed a unit vector and orthogonal to the basis vectors.
🏟️ Torus Surface Normal Vector Calculation
In the final paragraph, the script introduces a substitution to simplify the calculation of the normal vector for a torus surface. It applies the same technique used for the other surfaces, drawing lines through specific rows to form and subtract products, leading to the normal vector components. The script concludes with the normal vector components for the torus and suggests that the viewer confirm the vector's unit nature and orthogonality to the basis vectors.
Mindmap
Keywords
💡Tensor Calculus
💡Normal Components
💡Epsilon (Levi-Civita Symbol)
💡Shift Tensors
💡Surface Coordinates
💡Volume Element
💡Cross Product
💡Curl
💡Permutation
💡Coordinate Systems
💡Unit Vector
Highlights
Deriving the formula for the normal components of sample surfaces using tensor calculus.
Unpacking the formula into a more convenient form to save time in evaluating the normal for any given surface.
Using the epsilon tensor and volume elements to express the normal formula.
Evaluating the normal components for each index by considering permutations and dummy indices.
Simplifying the normal components by combining identical terms and considering the sign of permutations.
Applying the derived normal formula to specific coordinate systems like cylindrical, spherical, and torus surfaces.
Calculating the normal vector components for a cylindrical surface using the model forms.
Verifying the normal vector is a unit vector by checking the dot product with itself.
Demonstrating orthogonality of the normal vector with the basis vectors of the surface.
Using a geometric pattern to simplify the calculation of normal components by inspection.
Evaluating the normal vector for a spherical surface and simplifying the components.
Confirming the spherical normal vector is a unit vector and orthogonal to the basis vectors.
Making a substitution to simplify calculations for the torus surface normal components.
Calculating the normal vector components for a torus surface using the simplified method.
Confirming the torus normal vector is a unit vector and orthogonal to the basis vectors.
Highlighting the importance of understanding tensor calculus for evaluating surface normals in various coordinate systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: