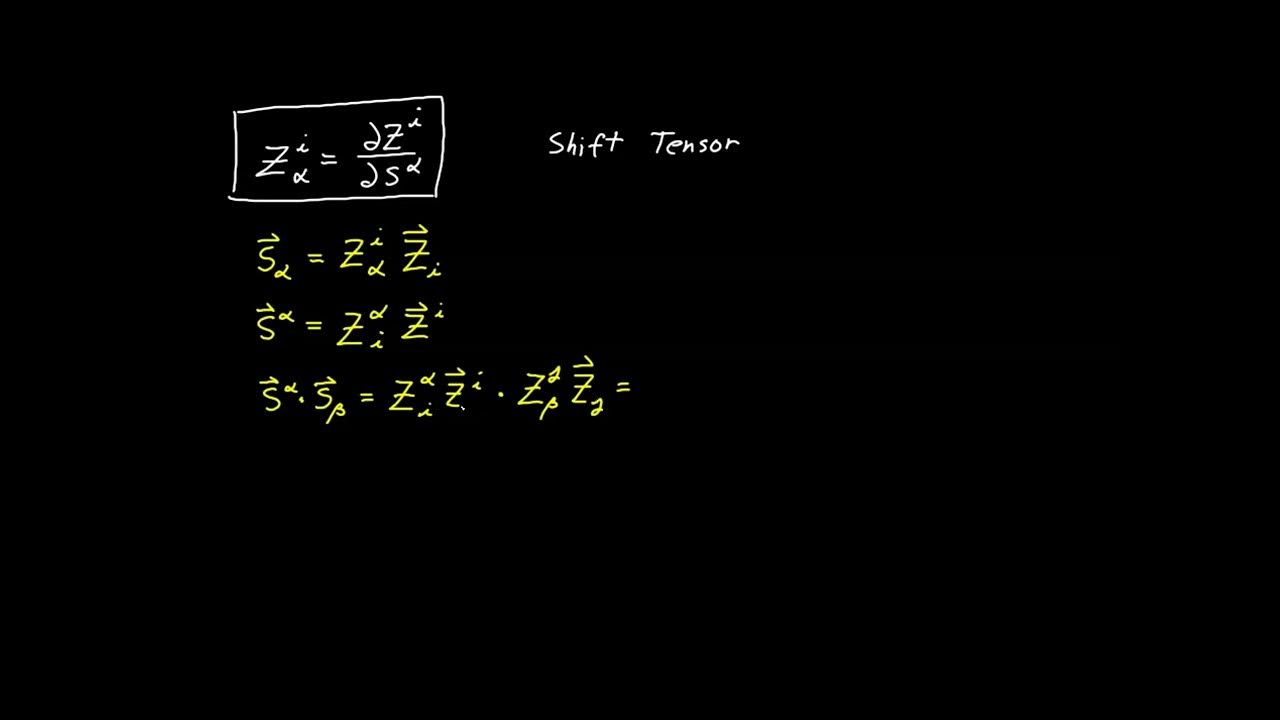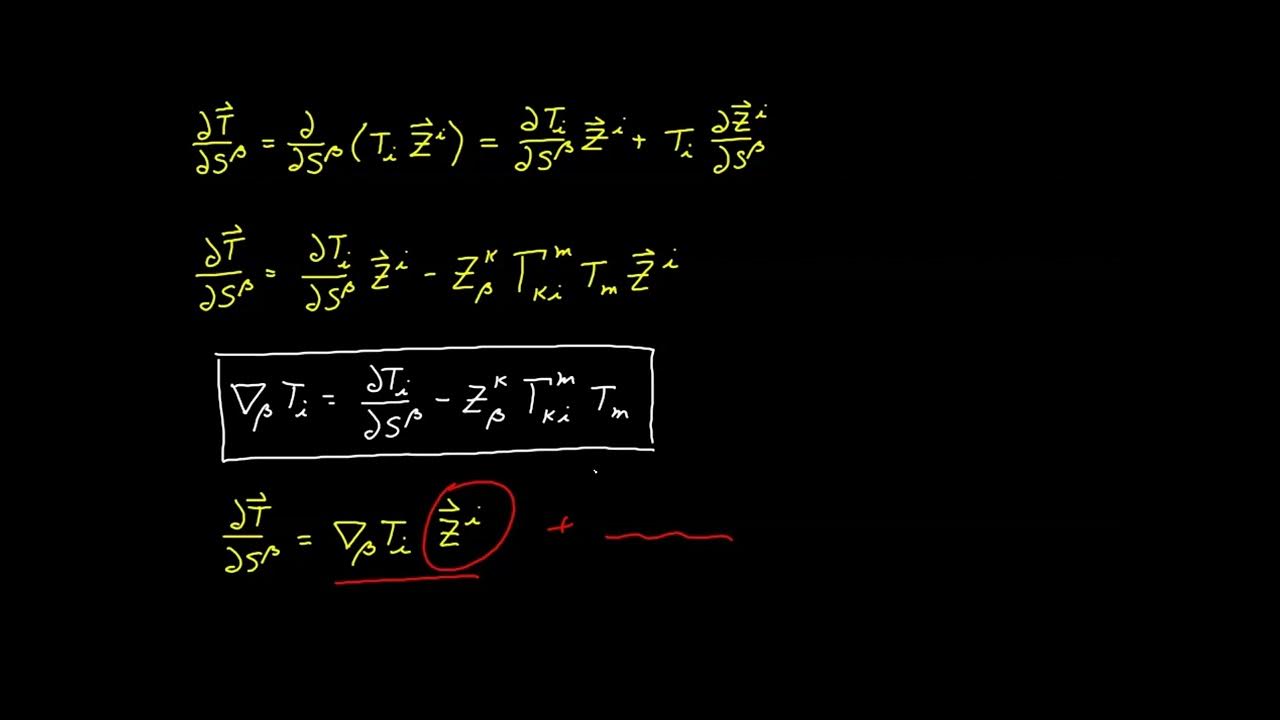Video 58 - Tangent Space
TLDRThis video delves into the concept of the tangent space in tensor calculus, essential for analyzing vectors and tensors relative to surface coordinates. It introduces surface coordinates, s1 and s2, and demonstrates how to relate them to ambient space coordinates using parametric equations. The script explains the derivation of basis vectors and the normal vector to establish the tangent plane and space, applicable to surfaces like cylinders, spheres, and tori. The video emphasizes the generalizability of these concepts to any sub-manifold within a Euclidean space.
Takeaways
- 📚 The video discusses the concept of the tangent space, which is essential for analyzing vectors and tensors relative to a surface's coordinates.
- 📐 The surface is described as a two-dimensional sub-manifold embedded in a three-dimensional Euclidean space, requiring a two-dimensional coordinate system for analysis.
- 🔠 Surface coordinates are labeled with s1 and s2 to distinguish them from the ambient space coordinates z1, z2, and z3.
- 🔄 Parametric equations are used to relate surface coordinates to ambient coordinates, with the equations expressed as z1, z2, and z3 as functions of s1 and s2.
- 🧩 Tensor calculus allows for the consolidation of parametric equations into a single form, simplifying the expression of these relationships.
- 📉 The video demonstrates the process of deriving basis vectors from a position vector using partial derivatives with respect to surface coordinates.
- 📊 Basis vectors are tangent to the coordinate lines on the surface and define the tangent plane, which is crucial for analyzing vectors and tensors within the tangent space.
- 📍 A normal vector is introduced, which is perpendicular to the tangent plane and has a unit length, providing an additional basis for vectors not lying in the tangent plane.
- ⚙️ The normal vector is derived based on its orthogonality to the surface basis vectors and its unit length property, often obtained by the cross product of the basis vectors.
- 🌐 The tangent space, composed of the basis vectors and the normal, provides a framework for analyzing vectors and tensors in relation to the surface coordinates.
- 🌀 The video uses specific examples, such as a cylinder, sphere, and torus, to illustrate the application of the concepts of tangent space, basis vectors, and normals in different contexts.
Q & A
What is the concept of the tangent space in the context of tensor calculus?
-The tangent space is a framework used to analyze vectors and tensors relative to a surface's coordinates. It is the set of all tangent vectors to the points of a manifold, and it provides a way to perform local analysis on the manifold.
Why is a two-dimensional coordinate system necessary to analyze points on a surface?
-A two-dimensional coordinate system is necessary because the surface is a two-dimensional sub-manifold embedded in a three-dimensional Euclidean space. Each point on the surface can be uniquely identified by two surface coordinates.
What is the difference between surface coordinates and ambient space coordinates?
-Surface coordinates (e.g., s1 and s2) are used to describe points on the surface of a manifold, while ambient space coordinates (e.g., z1, z2, and z3) represent the coordinates of the surrounding Euclidean space in which the manifold is embedded.
How are parametric equations used to relate surface coordinates to ambient coordinates?
-Parametric equations are functions that express each ambient coordinate (z1, z2, z3) as a function of the surface coordinates (s1, s2). By substituting the values of surface coordinates into these functions, one can find the corresponding ambient space coordinates of a point on the surface.
What is the significance of using tensor calculus to express parametric equations?
-Tensor calculus allows for the consolidation of parametric equations into a single, concise form using a free index. This makes it easier to handle and manipulate the equations, regardless of the number of dimensions involved.
Why can't an inverse relationship be derived from surface coordinates to ambient coordinates?
-An inverse relationship cannot be derived because not all points in the ambient space lie on the surface. It's impossible to express surface coordinates as a function of ambient coordinates since some ambient points do not correspond to any point on the surface.
How are basis vectors derived using surface coordinates?
-Basis vectors are derived by taking the partial derivative of the position vector with respect to each surface coordinate. This operation yields vectors that are tangent to the coordinate lines on the surface and form a basis for vectors and tensors in the tangent plane.
What is the role of the normal vector in defining the tangent space?
-The normal vector is perpendicular to the tangent plane and has a length of one (it's a unit vector). It is defined by its orthogonality to the basis vectors and its unit length. Together with the basis vectors, the normal vector establishes the tangent space, allowing for the analysis of any vector or tensor with respect to the surface coordinates.
How does the cross product of the basis vectors help in deriving the normal vector?
-The cross product of the basis vectors (s1 and s2) gives a vector that is perpendicular to both basis vectors, which is a requirement for the normal vector. Dividing this vector by its magnitude ensures it becomes a unit vector, fulfilling the second requirement for the normal.
What is the significance of the external normal in the context of bounded surfaces?
-The external normal is the normal vector that points outward from the bounded surface. It is customary to use the external normal when dealing with bounded surfaces like a sphere because it provides a consistent direction for the normal vector, which is useful in various calculations and analyses.
Outlines
📚 Introduction to Tangent Space in Tensor Calculus
This paragraph introduces the concept of the tangent space, which is essential for analyzing vectors and tensors in relation to surface coordinates. The video explains the need for a two-dimensional coordinate system to analyze points on a surface embedded in a three-dimensional Euclidean space. Surface coordinates (s1 and s2) are distinguished from ambient space coordinates (z1, z2, and z3). The challenge is to relate these surface coordinates to the ambient coordinates using parametric equations. The paragraph also touches on the use of tensor calculus to consolidate these equations into a single expression, making it applicable to any number of dimensions.
🔍 Parametric Equations and Coordinate Transformations
The paragraph delves into the process of using parametric equations to relate surface coordinates to ambient coordinates, comparing it to coordinate transformations previously discussed in video 6. It emphasizes the inability to derive an inverse relationship due to the nature of the surface not encompassing all points in the ambient space. The focus then shifts to representing vectors and tensors using surface coordinates, which involves deriving basis vectors from a position vector in the ambient space. The paragraph also explains the use of partial derivatives to obtain these basis vectors, which are tangent to the coordinate lines on the surface.
📐 Establishing Basis Vectors and the Tangent Plane
This section discusses the establishment of basis vectors by taking partial derivatives of the position vector with respect to surface coordinates. These basis vectors, which are tangent to the coordinate lines, define the tangent plane at a point on the surface. The paragraph introduces the concept of using Greek letters for surface indices to distinguish them from ambient space indices. It also highlights the importance of the tangent plane as a basis for vectors and tensors that lie exclusively within it.
🌐 Introducing the Normal Vector and Tangent Space
The paragraph introduces the normal vector, which is perpendicular to the tangent plane and has a unit length. It explains the properties of the normal vector, including its orthogonality to the surface basis vectors and its unit magnitude. The normal vector, derived from the cross product of the basis vectors, is crucial for defining the tangent space, which is the framework for analyzing vectors and tensors in general with respect to surface coordinates. The paragraph also touches on the convention of choosing the external normal for bounded surfaces.
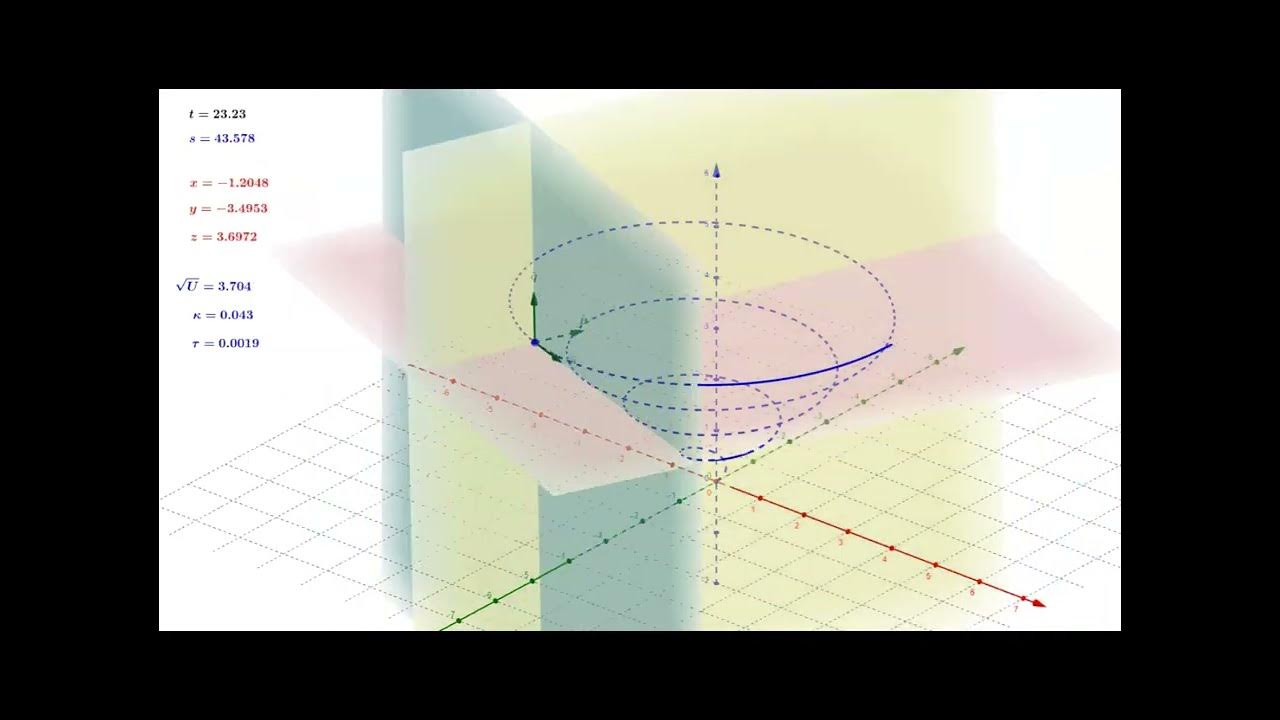
📘 Examples of Tangent Spaces on Different Surfaces
This paragraph provides specific examples of how to establish tangent spaces on various surfaces, such as a cylinder, a sphere, and a torus. It describes the process of defining surface coordinates, setting up parametric equations, displaying coordinate lines, and establishing basis vectors and normals for these surfaces. The examples illustrate how the tangent space moves with the point on the surface and how it is defined for each case.
🔚 Recap and Generalization of Tangent Space Concepts
The final paragraph recaps the key concepts discussed in the video, emphasizing the generalizability of the developed methods to any dimensionality of sub-manifolds within Euclidean spaces. It summarizes the process of developing parametric descriptions for surfaces, defining surface covariant basis vectors, and establishing the normal and tangent space. The paragraph concludes by reminding viewers that while the development is presented for two-dimensional surfaces, the principles apply to any abstract level.
📘 Generalization of Tangent Spaces for Higher Dimensions
The last paragraph of the script extends the concept of tangent spaces to higher-dimensional ambient spaces. It explains that the same principles used for two-dimensional surfaces can be applied to hypersurfaces in four-dimensional spaces or any other dimensionality. The paragraph highlights the adaptability of the equations and methods to define basis vectors and the normal, which together constitute the tangent space, regardless of the number of dimensions involved.
Mindmap
Keywords
💡Tangent Space
💡Surface Coordinates
💡Parametric Equations
💡Ambient Space
💡Basis Vectors
💡Tangent Plane
💡Normal Vector
💡Tensor Calculus
💡Coordinate Transformation
💡Sub-manifold
Highlights
Introduction of the concept of the tangent space as a framework for analyzing vectors and tensors relative to surface coordinates.
Explanation of the surface as a two-dimensional sub-manifold embedded in a three-dimensional Euclidean space.
Introduction of surface coordinates (s1 and s2) to distinguish from ambient space coordinates (z1, z2, and z3).
Use of parametric equations to relate surface coordinates to ambient coordinates in tensor calculus.
Consolidation of parametric equations into a single tensor calculus expression using a free index.
Extension of the concept of parametric equations for curves to surfaces in multi-variable functions.
Development of a method to represent vectors and tensors using surface coordinates through basis vectors.
Inability to establish a position vector on a curved surface, necessitating the use of a position vector from the ambient space.
Derivation of basis vectors through partial derivatives of the position vector with respect to surface coordinates.
Use of tensor calculus syntax to express the relationship between basis vectors and position vector concisely.
Customary use of Greek letters for indices in tensor calculus when dealing with surfaces.
Definition of the tangent plane by basis vectors that are tangent to their corresponding coordinate lines.
Introduction of the normal vector, perpendicular to the tangent plane, as part of the tangent space framework.
Properties of the normal vector: perpendicular to basis vectors and being a unit vector.
Derivation of the normal vector through the cross product of basis vectors and normalization.
Customary choice of the external normal for bounded surfaces, pointing outward from the surface.
Generalization of the developed concepts for surfaces to sub-manifolds of any size in higher-dimensional spaces.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: