Video 50 - Voss Weyl Examples

Tensor Calculus

5 Jun 202224:51

EducationalLearning

32 Likes 10 Comments

TLDRThis video script from the Tensor Calculus series explores the divergence and Laplacian in various coordinate systems, starting with Cartesian coordinates where the process is simplified due to the constant volume element. It then delves into affine, plane polar, cylindrical polar, and spherical polar coordinates, explaining the complexities and cancellations in each system. The script emphasizes the practicality of using the VoS Mial formula for deriving these expressions, showcasing the step-by-step process and normalization techniques for a comprehensive understanding.

Takeaways

📚 The video discusses the application of the VoS-Vial formula to understand the divergence and Laplacian in various coordinate systems, starting with Cartesian coordinates.
🧩 In Cartesian coordinates, the volume element is constant, simplifying the divergence calculation to the partial derivatives of vector components with respect to their respective coordinates.
🔍 For the Laplacian in Cartesian coordinates, the formula simplifies to the sum of second derivatives of a scalar function with respect to each coordinate variable.
🔄 Moving to affine coordinates, the divergence formula involves partial derivatives of vector components with respect to affine coordinates, with the volume element still being constant.
🌐 The Laplacian in affine coordinates is more complex, involving mixed partial derivatives and factors related to the coordinate transformation.
📊 In plane polar coordinates, the volume element is not constant, leading to a more involved formula for divergence without simplification.
📐 Normalizing the divergence and Laplacian expressions in plane polar coordinates involves considering the unit vectors and basis vectors specific to the coordinate system.
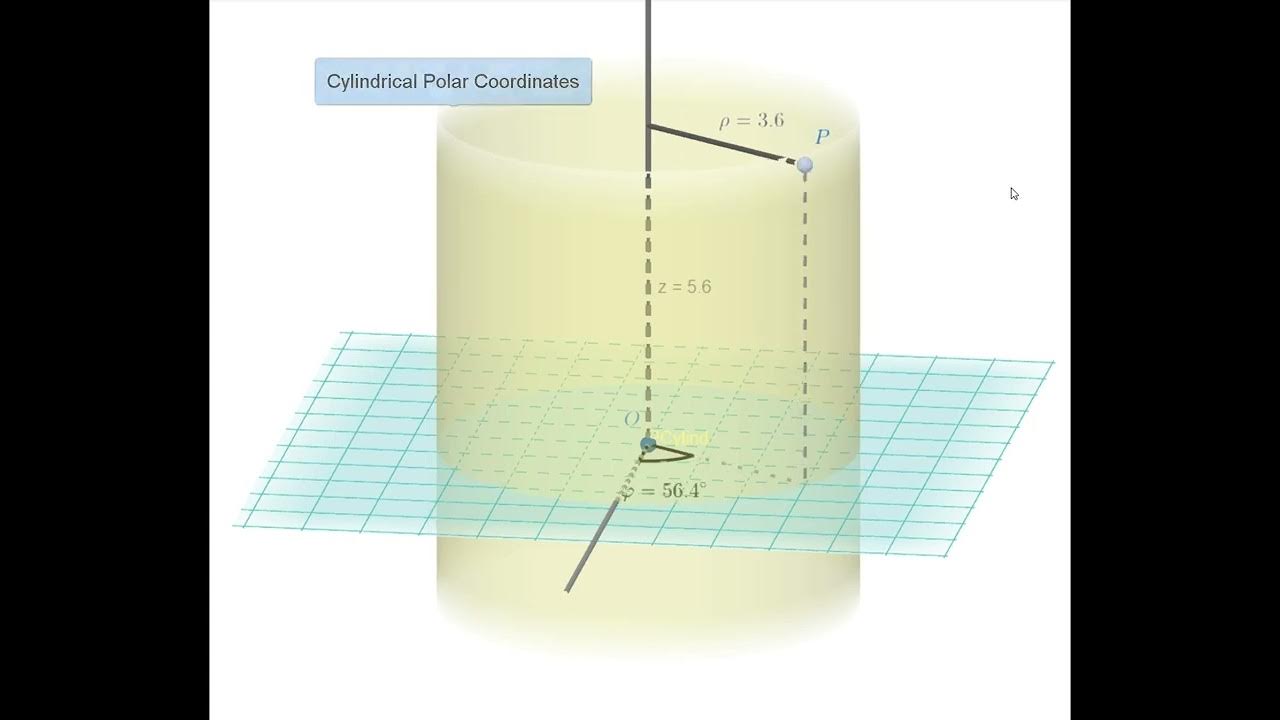
📈 Cylindrical polar coordinates share similarities with plane polar coordinates, with the divergence and Laplacian including additional terms due to the cylindrical nature of the system.
🌍 Spherical polar coordinates present the most complex scenario, with the divergence and Laplacian requiring careful handling of the volume element and basis vectors' magnitudes.
🧬 The video emphasizes the practicality of using the VoS-Vial formula for deriving expressions for divergence and Laplacian in various coordinate systems compared to the original forms.
🔗 The script concludes by highlighting the importance of understanding the cancellation of terms and the role of the volume element in simplifying tensor calculus operations across different coordinate systems.

Q & A

What is the volume element in Cartesian coordinates and why is it significant for divergence calculation?
-In Cartesian coordinates, the volume element is a constant, typically represented as 'dV'. Its significance in divergence calculation is that it allows simplification of the divergence formula by moving outside the differentiation and canceling out certain terms, leading to a simpler expression for divergence.
How does the divergence formula in Cartesian coordinates simplify when using the volume element?
-The divergence formula simplifies to the partial derivatives of the vector components with respect to their respective coordinates, because the volume element, being a constant, cancels out certain terms in the formula.
What is the expression for the Laplacian in Cartesian coordinates?
-The Laplacian in Cartesian coordinates is the sum of the second derivatives of the scalar function with respect to each coordinate variable, resulting from the simplification due to the constant volume element.
What changes occur in the divergence and Laplacian formulas when moving from Cartesian to affine coordinates?
-In affine coordinates, the divergence formula changes to include the partial derivatives of the vector components with respect to new coordinates, such as 'u' and 'v'. The Laplacian becomes more complex, involving mixed partial derivatives and factors related to the affine transformation.
How is the divergence formula derived for plane polar coordinates?
-In plane polar coordinates, the volume element is not constant, so the formula is applied as is, without cancellation. The divergence involves the partial derivative of the radial component with respect to 'r' and the azimuthal component with respect to 'theta', each multiplied by appropriate factors.
What is the significance of normalizing the divergence expression in plane polar coordinates?
-Normalizing the divergence expression in plane polar coordinates allows for expressing the vector in terms of unit vectors and basis vectors, which simplifies the expression and makes it easier to interpret physically.
What are the steps involved in deriving the Laplacian for cylindrical polar coordinates?
-The steps involve applying the Laplacian formula to the contravariant components of the gradient, considering the non-constant nature of the volume element in cylindrical polar coordinates, and simplifying the expression by canceling out terms where appropriate.
How does the divergence formula differ in spherical polar coordinates compared to other coordinate systems?
-In spherical polar coordinates, the divergence formula is more complex due to the non-constant volume element and involves terms with 'r', 'theta', and 'phi'. It requires careful handling of the partial derivatives and the factors involving 'r', 'sine(theta)', and 'cosine(phi)'.
What is the final expression for the Laplacian in spherical polar coordinates?
-The final expression for the Laplacian in spherical polar coordinates includes terms with second partial derivatives with respect to 'r', 'theta', and 'phi', each multiplied by appropriate factors that account for the coordinate system's geometry.
Why is the Voss-Weyl formula more practical for deriving expressions like divergence and Laplacian in various coordinate systems?
-The Voss-Weyl formula is more practical because it provides a unified approach to derive these expressions across different coordinate systems, simplifying the process and making it easier to understand the underlying mathematical structure.

Outlines

00:00

📚 Introduction to Divergence and Laplacian in Tensor Calculus

This paragraph introduces the application of the Voss-Misner formula in tensor calculus to calculate divergence and Laplacian in various coordinate systems. It begins with Cartesian coordinates, where the volume element is constant, simplifying the divergence to the partial derivatives of the vector's x, y, and z components with respect to their respective variables. The Laplacian is derived from the gradient, resulting in second derivatives with respect to each coordinate. The process is straightforward due to the constant volume element in Cartesian coordinates.

05:02

🔍 Divergence and Laplacian in Affine Coordinates

The second paragraph delves into the calculation of divergence and Laplacian in affine coordinates. The volume element remains constant, leading to a simplified divergence formula involving partial derivatives of the vector components with respect to their corresponding coordinates. The Laplacian is more complex, requiring the computation of partial derivatives of the contravariant components of the gradient and combining them with additional terms. The resulting expression for the Laplacian in affine coordinates is presented, showcasing the interplay of constants and variables in tensor calculus.

10:03

🌐 Exploring Divergence and Laplacian in Plane Polar Coordinates

In this paragraph, the discussion shifts to plane polar coordinates, where the volume element is no longer constant, necessitating a direct application of the formula without simplification. The divergence is derived by considering the partial derivatives with respect to r and θ, with the latter involving a factor of 1/r. The Laplacian is similarly derived, with the expression for the contravariant components of the gradient used to find second derivatives. The paragraph also touches on the concept of normalizing vector expressions in tensor calculus.

15:03

📉 Divergence and Laplacian in Cylindrical Polar Coordinates

The fourth paragraph examines the divergence and Laplacian in cylindrical polar coordinates, which are similar to plane polar coordinates but with an additional term for the z-component. The divergence is calculated by considering the partial derivatives with respect to ρ, φ, and z, with certain terms canceling out due to the constant nature of ρ in relation to φ and z. The Laplacian is derived in a similar manner, with the partial derivatives of the contravariant components of the gradient leading to second derivatives with respect to ρ, φ, and z. Normalization of the expressions is also discussed, emphasizing the role of unit vectors in cylindrical coordinates.

20:05

🌍 Spherical Polar Coordinates: Divergence and Laplacian

The final paragraph concludes the series with an exploration of divergence and Laplacian in spherical polar coordinates. The process involves a more complex set of partial derivatives due to the three-dimensional nature of the coordinate system. The divergence is derived by considering the partial derivatives with respect to r, θ, and φ, with terms canceling out where appropriate. The Laplacian is similarly derived, with the volume element and its relationship to the coordinate variables playing a crucial role in simplifying the expression. The paragraph emphasizes the practicality of using the Voss-Misner formula for these calculations.

Mindmap

Keywords

💡Divergence

Divergence is a vector calculus operation that measures the rate at which a vector field spreads out from a point. In the video, divergence is explored across different coordinate systems like Cartesian, affine, and polar coordinates. The concept is key to understanding how vector fields behave in various geometries, which is essential for applying tensor calculus in physics and engineering contexts.

💡Laplacian

The Laplacian is a second-order differential operator that applies to scalar fields, providing a measure of the field's curvature. In the video, the Laplacian is derived for several coordinate systems, showing how it simplifies or becomes more complex depending on the geometry. The Laplacian is significant in physics, particularly in solving problems related to heat conduction, electrostatics, and quantum mechanics.

💡Volume Element

A volume element is a small region of space used in calculus to perform integration over a given volume. The video explains how the volume element affects the divergence and Laplacian, particularly when it is a constant or when it varies with the coordinate system. This concept is crucial for integrating functions over different geometrical shapes, which is common in fields like fluid dynamics and electromagnetism.

💡Cartesian Coordinates

Cartesian coordinates are a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates. In the video, Cartesian coordinates are used as the starting point for deriving divergence and Laplacian, highlighting their simplicity when the volume element is a constant. Cartesian coordinates are fundamental in mathematics and physics due to their straightforward application to most problems.

💡Affine Coordinates

Affine coordinates are a generalization of Cartesian coordinates, often used when dealing with non-Euclidean spaces. In the video, affine coordinates are introduced to show how divergence and Laplacian are computed when the volume element is still constant but the coordinate system is more complex. This concept is important for understanding geometrical transformations and linear algebra in more advanced mathematical contexts.

💡Gradient

The gradient is a vector that represents the rate and direction of the fastest increase of a scalar field. The video discusses the gradient in the context of the Laplacian, showing how the components of the gradient are used to derive this operator in various coordinate systems. Understanding the gradient is essential for interpreting how scalar fields change in space, which is a core concept in multivariable calculus.

💡Contravariant Components

Contravariant components refer to the components of a vector in a coordinate system that transform oppositely to the basis vectors during a change of coordinates. The video uses this concept to derive the Laplacian, emphasizing the importance of correctly handling these components in tensor calculus. This concept is key in differential geometry and the theory of relativity, where transformations between different coordinate systems are common.

💡Spherical Polar Coordinates

Spherical polar coordinates are a three-dimensional coordinate system where the position of a point is determined by a radius and two angles. The video explores how divergence and Laplacian are computed in this coordinate system, particularly noting how the volume element is not constant. Spherical coordinates are widely used in physics, especially in problems involving spherical symmetry, such as gravitational fields or atomic orbitals.

💡Normalization

Normalization refers to the process of adjusting the components of a vector or a scalar field to ensure they adhere to certain criteria, such as unit length. In the video, normalization is discussed in the context of transforming vector components in different coordinate systems to their normalized forms. This step is crucial for ensuring that the physical interpretations of the vectors remain consistent across different mathematical frameworks.

💡Vosm Formula

The Vosm formula is a method used to simplify the derivation of divergence and Laplacian in various coordinate systems by taking advantage of the properties of the volume element. The video demonstrates how using the Vosm formula makes the derivation process more efficient, particularly in complex geometries. Understanding this formula is important for anyone working with differential operators in non-standard coordinate systems.

Highlights

Application of the Volterra-Vial formula to determine the divergence and Laplacian in various coordinate systems.

Simplification of divergence in Cartesian coordinates due to the constant volume element.

Derivation of the divergence expression as the partial derivative of vector components with respect to their respective coordinates in Cartesian coordinates.

Introduction of the Laplacian formula and its simplification in Cartesian coordinates due to the constant volume element.

Explanation of the Laplacian as the sum of second derivatives of a scalar function with respect to each coordinate variable in Cartesian coordinates.

Transition to affine coordinates and the impact of the constant volume element on the divergence formula.

Expression for divergence in affine coordinates involving partial derivatives of vector components with respect to affine coordinates.

Complexity increase in the Laplacian formula for affine coordinates due to the non-constant nature of the volume element.

Derivation of the Laplacian in affine coordinates as a combination of second partial derivatives with additional factors.

Introduction of plane polar coordinates and the non-constant volume element leading to a more complex divergence formula.

Normalization of the divergence expression in plane polar coordinates by incorporating unit vectors.

Explanation of the Laplacian in plane polar coordinates involving second partial derivatives with respect to r and theta.

Transition to cylindrical polar coordinates and the similarity to plane polar coordinates with an additional z-component.

Normalization of the divergence expression in cylindrical polar coordinates with consideration of unit vectors and magnitude factors.

Derivation of the Laplacian in cylindrical polar coordinates including second partial derivatives with respect to rho, phi, and z.

Introduction of spherical polar coordinates and the unique volume element impacting the divergence and Laplacian formulas.

Normalization of the divergence expression in spherical polar coordinates by accounting for the magnitude of the basis vectors.

Complex derivation of the Laplacian in spherical polar coordinates involving multiple second partial derivatives and trigonometric functions.

Transcripts

Browse More Related Video

Video 40 - Gradient Examples

Video 31 - Christoffel Symbol Examples

Video 56 - Cross Product & Curl Examples

Video 12 - Jacobian Examples

Video 25 - Dot Product Examples

Video 05 - Curvilinear Coordinates

Related Tags

Tensor Calculus Voss-Weyl Divergence Laplacian Cartesian Affine Polar Cylindrical Spherical Mathematics Educational