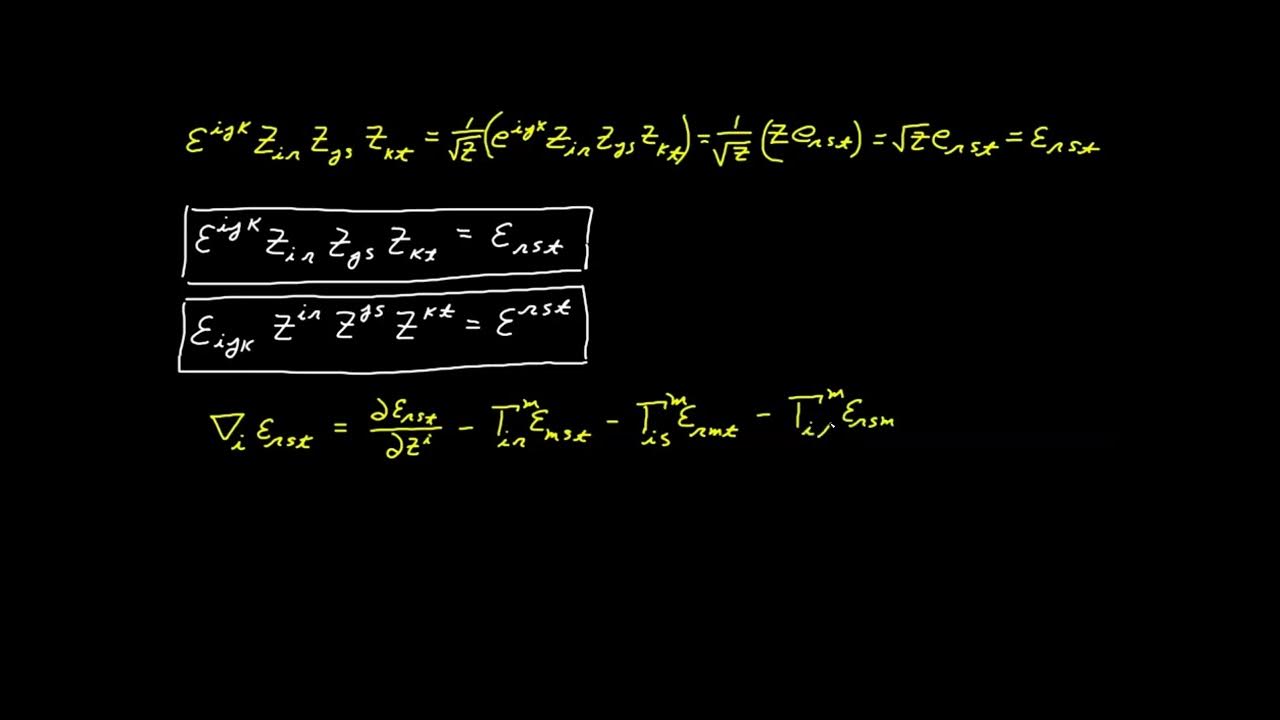Quotient Law for Tensors and Levi-Civita Symbol
TLDRThis video script from Brilliant.org offers an in-depth exploration of tensors, focusing on the quotient theorem and the Levi-Civita symbol. It explains the quotient theorem's proof, which establishes the rank of a tensor resulting from the inner product of an entity and a vector. The script also delves into the Levi-Civita symbol's definition, its role in determining determinants of matrices, and its application in vector cross products. The video aims to clarify the distinction between tensors and pseudotensors, highlighting the Levi-Civita symbol's importance in advanced mathematical concepts.
Takeaways
- 📚 Brilliant.org offers interactive learning in computer science and math with a growing library of lessons.
- 💡 The platform is beneficial for mastering fundamentals and maintaining professional skills in a dynamic landscape.
- 🎓 The first 200 sign-ups for a 30-day free trial receive a 20% discount on the annual premium subscription.
- 📘 The video discusses the quotient theorem for tensors, which is a rule for determining the rank of a tensor resulting from an inner product.
- 🔍 The proof of the quotient theorem involves the use of transformation laws and the invariance of equations under coordinate transformations.
- 📉 The Levi-Civita symbol, also known as the permutation symbol, is introduced and used in the study of tensors.
- 🔢 The Levi-Civita symbol is defined based on the permutation of indices and can be positive, negative, or zero depending on the arrangement.
- 📊 The symbol is crucial for calculating determinants of matrices and cross products of vectors, simplifying complex mathematical operations.
- 🧩 The determinant of a 3x3 matrix can be calculated using the Levi-Civita symbol, as demonstrated with an example in the script.
- 🔄 The Levi-Civita symbol can be extended to higher dimensions for calculating determinants of larger matrices, but requires a higher order symbol.
- 🌀 The cross product of vectors and the curl of a vector field result in pseudo vectors, which are similar to vectors but have different transformation rules.
Q & A
What is Brilliant.org and how can it be beneficial for learning computer science and math?
-Brilliant.org is an interactive learning platform that offers thousands of lessons in computer science and math. It is beneficial as it provides a growing curriculum in various fields from the history of mathematics to artificial intelligence and programming neural networks, helping users to grasp fundamentals in an interactive and concise manner, which is useful for lifelong learning and professional development.
What is the Quotient Theorem for tensors and how does it relate to the inner product of an entity and a vector?
-The Quotient Theorem for tensors states that if a tensor 's' of contravariant rank 'P' and covariant rank 'Q' is created from the inner product of an entity 'T' and a vector 'v' with a single contravariant index 'k', then 'T' is also a tensor with a contravariant rank of 'P' and a covariant rank of 'Q Plus One'. This theorem is used to prove the properties of tensors under coordinate transformations.
Can you explain the transformation law used in the proof of the Quotient Theorem?
-The transformation law used in the proof of the Quotient Theorem is based on the assumption of a coordinate transformation between two coordinate systems. It involves equations that relate the default coordinates to the post-transformation coordinates. The proof uses these transformation laws to show that the tensor 'T' follows the transformation law for a tensor of rank 'P', comma 'Q Plus One', thus proving it is indeed a tensor of that rank.
What is the significance of the Levi-Civita symbol (Epsilon sub-ijk) in tensor calculus?
-The Levi-Civita symbol, also known as the permutation symbol, is significant in tensor calculus as it is used to define the properties of tensors based on the permutation of their indices. It is crucial for understanding determinants of matrices and cross products of vectors, among other applications.
How is the Levi-Civita symbol defined in terms of even and odd permutations?
-The Levi-Civita symbol is defined based on the arrangement of its indices. If the indices form an even permutation of 1, 2, and 3, the symbol is positive one. If they form an odd permutation, the symbol is negative one. If any of the indices are repeated, the symbol is zero.
What is the relationship between the Levi-Civita symbol and the cross product of two vectors?
-The Levi-Civita symbol is used to express the cross product of two vectors 'A' and 'B' in terms of their components. The cross product yields a vector 'C', and the components of 'A', 'B', and 'C' can be related through the Levi-Civita symbol, indicating that the cross product results in a pseudovector, not a true vector.
How can the Levi-Civita symbol be used to calculate the determinant of a 3x3 matrix?
-The determinant of a 3x3 matrix 'A' can be calculated using the Levi-Civita symbol by summing over the products of the matrix elements and the symbol, with the indices of the symbol running over the rows, columns, and the third dimension. This method extends to higher-order matrices but requires a higher-order version of the Levi-Civita symbol.
What is the difference between a tensor and a pseudotensor?
-A tensor is a mathematical object that follows specific transformation rules under coordinate changes. A pseudotensor, on the other hand, is similar to a tensor but follows slightly different transformation rules. Pseudotensors, such as the Levi-Civita symbol, are used in calculations involving determinants and cross products.
Why is the curl of a vector field considered a pseudovector?
-The curl of a vector field is considered a pseudovector because it is defined as the cross product of the gradient operator with the vector field. Since the Levi-Civita symbol, which is used in the definition of the cross product, is a pseudotensor, the result of the cross product is also a pseudovector.
How can the concepts discussed in the script be applied to further understand tensor calculus?
-The concepts discussed in the script, such as the Quotient Theorem, the transformation laws, and the Levi-Civita symbol, are fundamental to understanding tensor calculus. They provide the framework for analyzing tensors under different coordinate systems, calculating determinants and cross products, and comprehending the properties of pseudotensors and pseudovectors.
Outlines
📚 Introduction to Brilliant.org and Tensors
This paragraph introduces the educational platform brilliant.org, which offers interactive learning in computer science and mathematics, with a vast array of lessons covering various topics from history to AI. It emphasizes the platform's utility for professional development and lifelong learning. The speaker then transitions into a lesson on tensors, specifically the quotient theorem and the Levi-Civita symbol, which are fundamental in tensor calculus. The lesson begins with a scenario involving the creation of a tensor from an inner product, setting the stage for the proof of the quotient theorem.
🔍 Proving the Quotient Theorem for Tensors
The speaker embarks on proving the quotient theorem using transformation laws and the invariance of equations under coordinate system changes. The proof involves expressing the tensor in terms of transformed coordinates and utilizing the inner product of an entity T with a vector v. By subtracting equations and factoring out common components, the proof demonstrates that T adheres to the transformation law for a tensor of increased rank, thereby confirming the quotient theorem.
📘 Understanding Even and Odd Permutations and the Levi-Civita Symbol
This section delves into permutations and their classification as even or odd based on the number of inversions. An even permutation has an even number of inversions, while an odd permutation has an odd number. The concept is applied to define the Levi-Civita symbol, denoted by Epsilon_ijk, which assigns values based on the permutation of indices. The symbol equals +1 for even permutations of 1, 2, and 3, -1 for odd permutations, and 0 if any indices are repeated. The speaker also introduces a visual aid for determining the permutation type using a triangle diagram and discusses the symbol's application in calculating determinants and cross products.
📐 Application of the Levi-Civita Symbol in Determinants and Vector Cross Products
The final paragraph discusses the application of the Levi-Civita symbol in calculating the determinant of a 3x3 matrix and the cross product of vectors. The determinant formula is presented, and an example calculation is provided, demonstrating the simplification process using the properties of the Levi-Civita symbol. The paragraph also touches on the extension of the determinant formula to n-dimensional matrices and the concept of pseudotensors, which are similar to tensors but follow different transformation rules. The video concludes with a brief mention of pseudovectors and an invitation for feedback from viewers.
Mindmap
Keywords
💡brilliant.org
💡tensor
💡quotient theorem
💡Levi-Civita symbol
💡permutation
💡determinant
💡cross product
💡pseudotensor
💡coordinate transformation
💡partial derivatives
Highlights
Brilliant.org offers interactive learning in computer science and math with a growing range of lessons.
The platform covers topics from the history of mathematics to artificial intelligence and programming neural networks.
Brilliant's computer science courses are designed to solidify fundamental concepts in an interactive and concise manner.
The platform is an excellent tool for lifelong learning and maintaining professional skills.
A 30-day free trial is available to experience all that Brilliant has to offer.
The first 200 sign-ups receive a 20% discount on the annual premium subscription.
The video discusses the quotient theorem for tensors, an essential concept in tensor calculus.
The Levi-Civita symbol, also known as the permutation symbol, is introduced for its utility in tensor studies.
The quotient theorem states that if a tensor is created from the inner product of an entity and a vector, it maintains tensor properties.
The proof of the quotient theorem involves the use of transformation laws and coordinate systems.
The transformation law is key to proving the invariance of tensor equations under coordinate transformations.
The video explains how to use barred variables to denote values post-transformation in tensor calculations.
The concept of even and odd permutations is crucial for understanding the Levi-Civita symbol.
The Levi-Civita symbol is defined based on the permutation of its indices, with specific values for even, odd, and repeated indices.
A diagram is provided to help determine the arrangement of indices for the Levi-Civita symbol as even or odd permutations.
The Levi-Civita symbol is applied in calculating determinants of 3x3 matrices and cross products of vectors.
The determinant of a 3x3 matrix can be calculated using the Levi-Civita symbol and the elements of the matrix.
The video demonstrates a determinant calculation example using the Levi-Civita symbol.
The Levi-Civita symbol can be extended to calculate determinants of n x n matrices with higher-order versions.
The Levi-Civita symbol is not a tensor but a pseudotensor, which follows different transformation rules.
The cross product of two vectors and the curl of a vector field are pseudovectors, not true vectors.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: