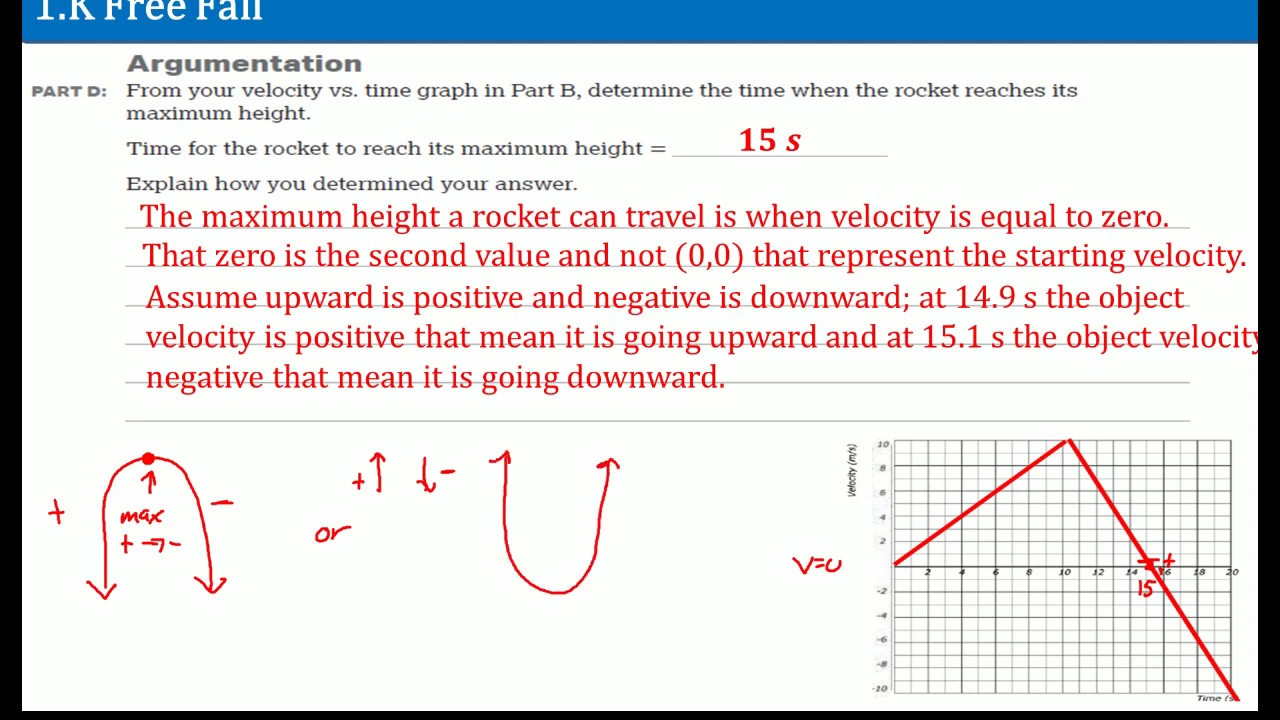
MIT Exam Challenge
TLDRThis transcript details the physics problem of a rocket moving through an interstellar dust cloud. It discusses the derivation of the rocket's equation of motion considering the mass of the rocket, fuel, and the force from particle collisions. The video provides a step-by-step solution, including how to maintain constant velocity and the velocity function if the rocket runs out of fuel. The problem involves Newton's second law, momentum change, and differential equations, offering an engaging exploration of rocket dynamics in space.
Takeaways
- 🚀 The problem involves a rocket moving at a constant speed entering an interstellar dust cloud.
- 📐 The total mass of the system is the sum of the rocket's mass and the fuel mass, minus the mass ejected.
- 🔧 Newton's second law is applied to derive the equation of motion, considering the net force and the change in momentum.
- ⏱️ The rocket emits fuel at a rate given by \( \frac{dM}{dt} \), which affects the system's momentum.
- 🌌 The force exerted by the dust cloud particles on the rocket is modeled as \( F = -AV^2 \).
- 📉 The rocket's mass changes over time due to fuel ejection, represented as \( M(t) \).
- 🚀🔧 To maintain a constant velocity, the thrust must balance the force from the dust cloud particles.
- 🛑 If the rocket runs out of fuel, the equation of motion changes to reflect the absence of fuel ejection.
- ⏳ The velocity of the rocket as a function of time after running out of fuel is derived from a differential equation.
- 🔄 The final equation for the rocket's velocity if it runs out of fuel is given by \( V_T = \frac{M_r V_0}{A t V_0 + M_r} \).
- 🤓 The script suggests that these types of problems are both challenging and enjoyable, encouraging further exploration.
Q & A
What is the initial constant speed of the rocket entering the interstellar dust cloud?
-The initial constant speed of the rocket is denoted as V_0 in the script.
What is the force exerted by the dust particles on the rocket?
-The force exerted by the dust particles is given by F = -AV^2, where A is a constant and V is the velocity of the rocket.
How is the mass of the rocket and its fuel described in the script?
-The total mass of the system, including the rocket and its fuel, is represented by M, which is a function of time due to the ejection of fuel.
What is the rate at which the rocket emits fuel?
-The rate at which the rocket emits fuel is given by dM/dt = γ.
What does the script suggest to do first to simplify the problem?
-The script suggests defining the total mass of the rocket and its remaining fuel as M(t) to simplify the problem.
What is the approach to tackle the problem according to the script?
-The approach is to use Newton's second law, which states that the net force equals the change in momentum over time (dP/dt).
How does the script describe the ejection of fuel and its effect on the rocket's speed?
-The script describes the ejection of a small amount of fuel DM at speed U with respect to the rocket, causing the rocket's mass M to increase its speed by DV.
What is the final equation of motion for the rocket derived in the script?
-The final equation of motion for the rocket is m dv/dt = γU - AV^2, where m is the mass of the rocket, v is its velocity, and γ is the rate of fuel ejection.
What must the rocket's thrust be to maintain a constant velocity according to the script?
-To maintain a constant velocity V_0, the thrust must be such that γU = AV_0^2, where γ is the rate of fuel ejection and U is the ejection speed of the fuel.
What happens to the rocket's velocity if it suddenly runs out of fuel?
-If the rocket runs out of fuel, the term dM/dt becomes zero, and the velocity of the rocket is given by the equation V_T = M_r V_0 / (1 + (A / M_r) t V_0), where M_r is the remaining mass of the rocket and t is the time after the fuel runs out.
What is the differential equation derived for the rocket's velocity if it runs out of fuel?
-The differential equation for the rocket's velocity after running out of fuel is dv/dt = -(A/m) V^2, which can be integrated to find the velocity as a function of time.
Outlines
🚀 Rocket Motion in Interstellar Dust Cloud
This paragraph discusses a problem involving a rocket moving at a constant speed through an interstellar dust cloud. The total mass of the system includes the rocket and its fuel. To counteract the force from particle collisions, the rocket emits fuel at a rate of \( \gamma \), which is \( \frac{dM}{dt} \). The problem is approached using Newton's second law, considering the change in momentum over a small time interval \( dt \). The rocket's mass is reduced as fuel is ejected at a relative speed \( U \). The change in momentum is calculated, leading to an equation of motion that relates the acceleration of the rocket to the ejection rate of fuel and the speed of the rocket. The final equation for the rocket's motion is derived, considering the mass \( m \) as a function of time.
🔧 Maintaining Constant Velocity with Rocket Thrust
In the second paragraph, the focus shifts to maintaining a constant velocity \( V_0 \) for the rocket. To achieve this, the acceleration must be zero, which is possible if the thrust force equals the opposing force due to fuel ejection. The thrust is calculated as \( \gamma U \), which is equated to \( a V^2 \), where \( a \) is the acceleration and \( V \) is the velocity. The units of thrust are derived from the units of \( \gamma \) and \( U \). The paragraph also addresses what happens if the rocket runs out of fuel, leading to a differential equation for the rocket's velocity as a function of time. The solution to this differential equation is found by separation of variables and integration, resulting in an equation that describes the rocket's velocity over time after fuel depletion.
Mindmap
Keywords
💡Rocket
💡Constant Speed (V naught)
💡Interstellar Dust Cloud
💡Mass
💡Fuel Ejection
💡Force (F)
💡Newton's Second Law
💡Momentum
💡Acceleration
💡Thrust
💡Differential Equation
Highlights
Derivation of the equation of motion for a rocket moving through an interstellar dust cloud.
Assumption of compensatory fuel emission to counteract the force from particle collisions.
Introduction of the mass of the rocket plus fuel minus ejected mass as a function of time, M(t).
Application of Newton's second law to find the change in momentum of the rocket system.
Consideration of the rocket's momentum change due to a small amount of fuel ejected at speed U.
Algebraic simplification of the momentum change equation to isolate terms for acceleration.
Substitution of the given force equation into the momentum change to find the rocket's acceleration.
Rearrangement of the acceleration equation to express it solely in terms of the rocket's parameters.
Explanation of how to maintain a constant velocity by balancing the thrust with the dust cloud's resistance.
Calculation of the required thrust to counteract the dust cloud's force and maintain velocity.
Derivation of the rocket's velocity as a function of time if it suddenly runs out of fuel.
Transformation of the motion equation into a differential equation for velocity when fuel is depleted.
Integration of the differential equation to find the velocity of the rocket over time without fuel.
Final expression for the rocket's velocity post-fuel depletion, showing its dependence on time and initial conditions.
Discussion on the practical implications of the derived equations for rocket propulsion and fuel management.
Highlighting the importance of understanding the interaction between a rocket and its environment for space travel.
Encouragement to explore further questions related to rocket dynamics for a deeper understanding of the subject.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: