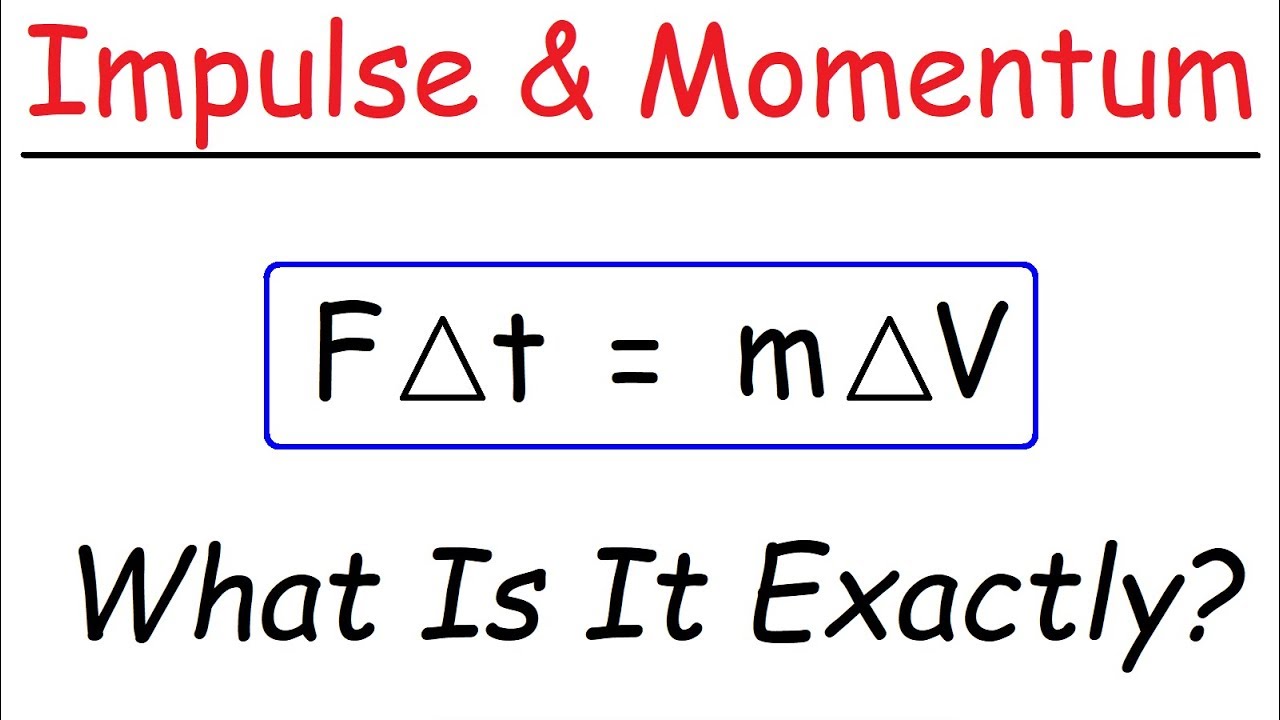Force-Time Graph

Bozeman Science
22 Oct 201405:56
EducationalLearning
32 Likes 10 Comments

TLDRIn this AP Physics essentials video, Mr. Andersen explains the concept of force-time graphs, using the Saturn 5 rocket as a practical example. He details the three stages of the rocket's launch, each with different force applications and durations, and how these translate into changes in momentum. The video emphasizes the relationship between impulse (force times time) and change in momentum, and demonstrates how to calculate changes in velocity based on force-time graphs, highlighting the importance of considering mass changes in real-world scenarios.

Takeaways
  • 🚀 The concept of a force-time graph is introduced, which illustrates the relationship between the force applied and the duration of its application.
  • 📈 The area under the force-time graph represents the impulse (measured in Joules), which is the product of force and time.
  • 🌙 The example of the Saturn 5 rocket's three stages is used to demonstrate how varying forces and durations contribute to the overall change in momentum.
  • 🔢 Impulse is equivalent to the change in momentum, which can be calculated as mass times the change in velocity.
  • 🛰️ The first stage of the Saturn 5 rocket applies a force of 34 million Newtons for 165 seconds.
  • 🔥 The second stage of the rocket has a lower force of 4 million Newtons but applies it for a longer duration of 360 seconds.
  • 🌠 The third stage exerts 1 million Newtons of force and fires twice: once to reach escape velocity and again to align with the moon's trajectory.
  • 📊 By analyzing the force-time graph, one can determine the change in momentum and subsequently calculate the change in velocity.
  • 🎓 In AP Physics, it is assumed that the mass remains constant when calculating changes in velocity, although in reality, the mass of a rocket decreases as fuel is burned.
  • 📝 The script provides a practical example of how to use the force-time graph to calculate the change in velocity of the Saturn 5 rocket, resulting in approximately 1900 meters per second.
  • 📚 The video also discusses how to break down complex force-time graphs into simpler geometric shapes to calculate the total impulse.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the force-time graph, which illustrates the relationship between the force applied and the duration of its application.

  • What is an example used in the video to explain the force-time graph?

    -The video uses the example of the Saturn 5 rocket, a three-stage rocket that was used to send Apollo astronauts to the moon.

  • How is the force-time graph represented in the video?

    -The force-time graph is represented as a graph where the force applied is plotted over time, and the area under the graph represents the impulse.

  • What is the significance of the area under the force-time graph?

    -The area under the force-time graph is equal to the impulse, which is represented by the unit Joules (J) and is related to the change in momentum of an object.

  • How does the change in momentum relate to the impulse?

    -The change in momentum is equivalent to the impulse, which is the product of the force applied and the time over which it is applied. Both are vector quantities and have the same direction.

  • What is the force applied during the first stage of the Saturn 5 rocket launch?

    -During the first stage of the Saturn 5 rocket launch, the force applied is 34 million newtons.

  • How long is the force applied in the first stage of the Saturn 5 rocket launch?

    -The force is applied for 165 seconds in the first stage of the Saturn 5 rocket launch.

  • What is the relationship between force, mass, and change in velocity according to the video?

    -According to the video, the force applied (F) times time (t) is equal to mass (m) times the change in velocity (Δv), which can be represented by the equation F*t = m*Δv.

  • How does the mass of the rocket affect the change in velocity?

    -As the rocket burns fuel, its mass decreases, which in turn increases the change in velocity for the same applied force and time, due to the inverse relationship between mass and velocity change in the momentum equation.

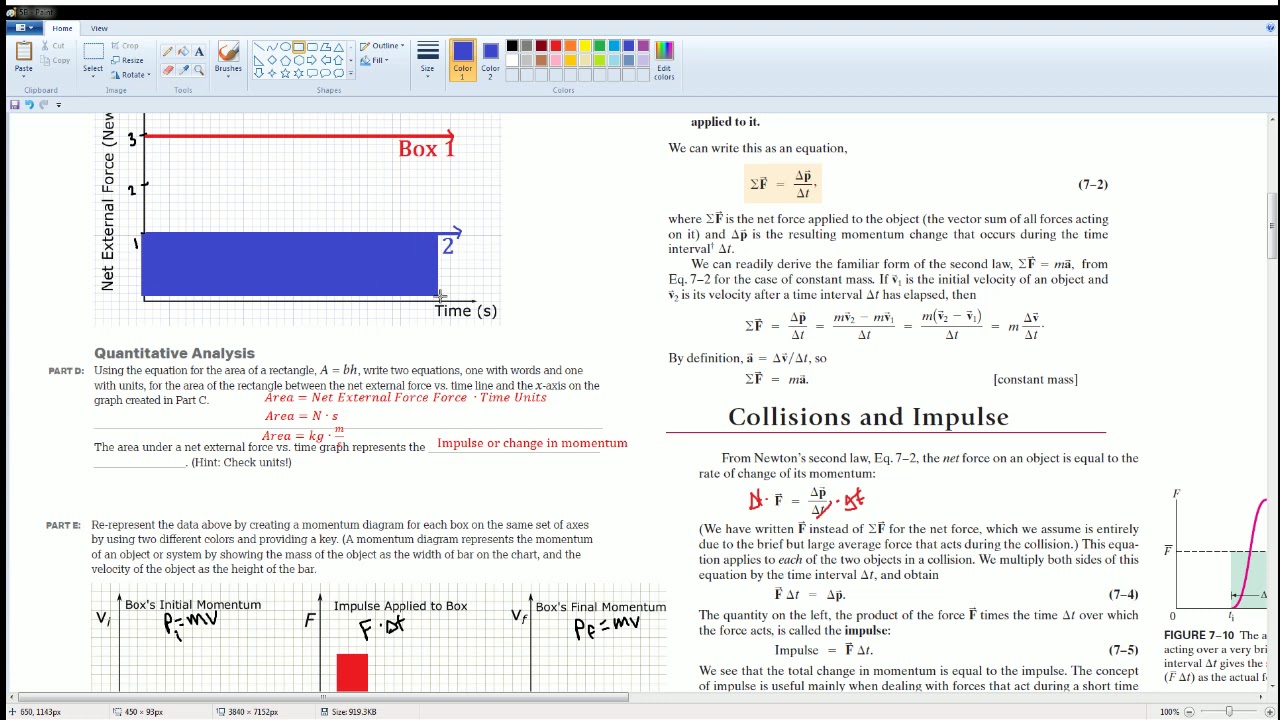
  • How can one calculate the change in momentum using a force-time graph?

    -To calculate the change in momentum using a force-time graph, one must calculate the area under the curve, which represents the impulse. This impulse is then related to the change in momentum through the equation impulse = change in momentum.

  • What is the final change in velocity calculated for the Saturn 5 rocket example in the video?

    -The final change in velocity calculated for the Saturn 5 rocket example is approximately 1900 meters per second, although NASA's value is higher at 2756 meters per second due to the decreasing mass of the rocket.

  • How can the principles discussed in the video be applied to solve problems in AP Physics?

    -The principles discussed in the video can be applied to solve problems in AP Physics by understanding the relationship between force, time, impulse, and change in momentum. Students can use force-time graphs to calculate changes in momentum and velocity given the mass of an object, assuming the mass remains constant.

Outlines
00:00
🚀 Introduction to Force-Time Graphs and Impulse

This paragraph introduces the concept of force-time graphs, using the example of the Saturn 5 rocket's three stages to illustrate how force is applied over time. It explains that the area under the force-time graph represents impulse (measured in Newton-seconds), which is equivalent to the change in momentum (mass times change in velocity). The paragraph also covers how to calculate the change in velocity given a force-time graph and a constant mass, using the Saturn 5 rocket as a real-world example to demonstrate the calculation.

05:01
📈 Analyzing Force-Time Graphs for Momentum Change

The second paragraph delves into how to analyze force-time graphs to determine changes in momentum. It presents a hypothetical scenario where the change in force over time is given, and the task is to calculate the momentum change. The paragraph explains how to break down the graph into geometric shapes to calculate the area under the curve, representing the impulse. It then relates this impulse to the change in momentum and provides a method to calculate the change in velocity if the mass is known, offering an interactive element for the viewer to solve the problem.

Mindmap
Keywords
💡Force-time graph
A force-time graph is a visual representation that illustrates the relationship between the force applied to an object and the duration for which it is applied. In the context of the video, it is used to analyze the three stages of a Saturn 5 rocket's launch, showing how the force changes over time and how this correlates with the rocket's momentum and velocity changes.
💡Impulse
Impulse is a measure of the change in momentum of an object when a force is applied over a period of time. It is calculated as the product of the force applied and the time over which it is applied, represented by the unit newton-seconds (N·s). In the video, impulse is used to analyze the rocket's change in momentum and velocity during its launch stages.
💡Momentum
Momentum is a physical quantity that represents the motion of an object, defined as the product of the object's mass and its velocity. It is a vector quantity, meaning it has both magnitude and direction. In the video, the change in momentum is central to understanding how the rocket's velocity changes as it ascends, with the impulse being equivalent to this change in momentum.
💡Change in velocity
Change in velocity refers to the difference in velocity of an object from an initial state to a final state. In the context of the video, it is the increase in the rocket's speed as a result of the force applied by its engines over time. The change in velocity is calculated using the impulse and the mass of the rocket, and it is a critical factor in determining the rocket's trajectory and ability to reach space.
💡Saturn 5 rocket
The Saturn 5 rocket is a historic launch vehicle used in the Apollo program to send astronauts to the moon. It is a three-stage rocket, with each stage providing a different amount of force over a different duration. The video uses the Saturn 5 as an example to explain the concepts of force-time graphs, impulse, and change in momentum and velocity.
💡Newton's second law
Newton's second law of motion states that the acceleration of an object is directly proportional to the net force acting upon it and inversely proportional to its mass. It is often expressed as F=ma, where F is force, m is mass, and a is acceleration. In the video, this law is used to connect the concepts of force, mass, acceleration, change in velocity, and ultimately, impulse and momentum.
💡Mass
Mass is a measure of the amount of matter in an object, and it is a fundamental property that determines the object's inertia and the gravitational force it experiences. In the context of the video, the mass of the rocket is crucial for calculating the change in velocity and understanding how the rocket's momentum changes as it ascends and burns fuel.
💡Three-stage rocket
A three-stage rocket is a type of launch vehicle that uses three separate engines or stages to propel itself into space. Each stage has its own fuel and engines, and they are ignited sequentially as the rocket ascends. The video uses the Saturn 5 rocket as an example of a three-stage rocket, explaining how the force and duration of each stage contribute to the overall momentum and velocity of the rocket.
💡Escape velocity
Escape velocity is the minimum speed an object must reach to break free from the gravitational pull of a celestial body, such as Earth, without further propulsion. In the video, it is mentioned in the context of the Saturn 5 rocket's third stage, which must achieve this velocity to send the spacecraft on a trajectory towards the moon.
💡Trajectory
Trajectory refers to the path that an object follows through space as it moves under the influence of various forces, such as gravity. In the context of the video, the trajectory is important for the rocket's third stage to ensure that it intersects with the moon after achieving escape velocity.
💡Data analysis
Data analysis involves the process of inspecting, cleaning, transforming, and modeling data to extract useful information, draw conclusions, and support decision-making. In the video, data analysis is used to interpret the force-time graph and calculate the impulse and change in momentum, which are essential for understanding the rocket's performance.
Highlights

The topic of the video is the force-time graph, which illustrates the relationship between the force applied and the duration of its application.

The Saturn 5 rocket, which carried Apollo astronauts to the moon, is used as an example to explain the force-time graph.

The Saturn 5 is a three-stage rocket with each stage having a different force and duration.

Stage 1 of the rocket applies a force of 34 million newtons for 165 seconds.

Stage 2 applies 4 million newtons of force over a period of 360 seconds.

Stage 3 applies 1 million newtons of force and fires twice, once for escape velocity and once for lunar trajectory.

The force-time graph for the first stage of the rocket is a representation of the impulse, measured in joules (J).

Impulse is equivalent to the change in momentum, which is mass times the change in velocity.

The area under the force-time graph represents the impulse, which can be used to calculate the change in momentum and velocity.

The second stage of the rocket has a longer duration, resulting in a greater change in momentum due to the extended application of force.

The change in linear momentum is equal to the mass times the change in velocity, which is also equal to the impulse (force times time).

Impulse and change in momentum are equivalent in units, with both measured in kilogram meters per second.

The force-time graph can be used to calculate the change in velocity of the Saturn 5 rocket, given its mass and the applied force over time.

The actual change in velocity calculated from the force-time graph (1900 m/s) is less than NASA's reported value (2756 m/s) due to the decreasing mass of the rocket as it burns fuel.

In AP Physics, questions will typically assume a constant mass for the purpose of calculating changes in velocity and momentum.

The video also covers how to calculate the change in momentum using a force-time graph by determining the area under the curve.

An example is provided to calculate the change in velocity given a force-time graph and the mass of the rocket.

The video aims to teach viewers how to calculate impulse (force times time), understand its equivalence to change in momentum, and perform data analysis on force-time graphs.

Transcripts

Browse More Related Video

Momentum

High School Physics - Impulse-Momentum Theorem

Position, Velocity and Acceleration

AP Physics Workbook 5.F Conservation of momentum in Elastic Collisions

Introduction to Impulse & Momentum - Physics

AP Physics Workbook 5.B Impulse

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics EssentialsForce-Time GraphImpulse CalculationMomentum ChangeAP PhysicsSaturn 5 RocketRocket PropulsionNewton's LawsData AnalysisEducational Content