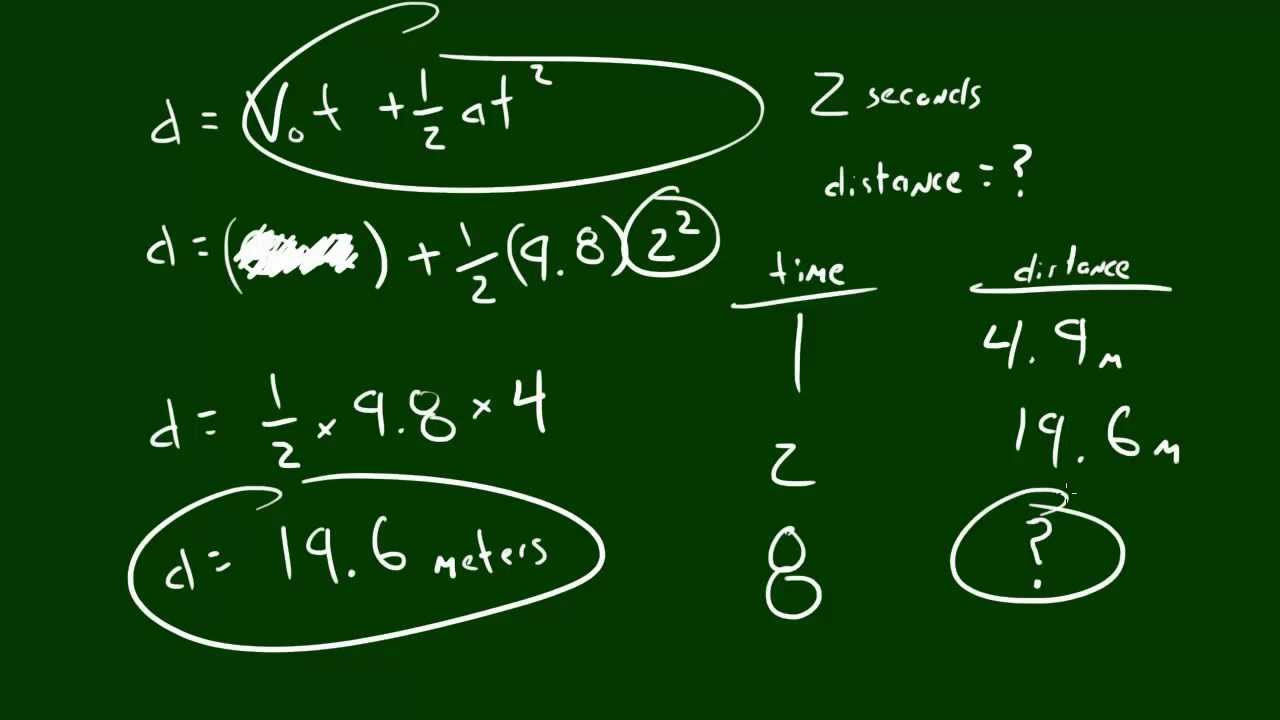AP Physics B Kinematics Presentation #34

The New Jersey Center for Teaching and Learning
26 Jun 201203:55
EducationalLearning
32 Likes 10 Comments

TLDRThis script explains the physics behind calculating the height of a house from which a water drop falls in 3 seconds. It uses the kinematic equations to determine the initial height, considering the initial velocity is zero and the acceleration due to gravity is 9.8 m/s². By simplifying the equation and substituting the given values, the script demonstrates how to find the house's height, concluding it to be approximately 44.1 meters.

Takeaways
  • 🏠 The problem involves calculating the height of a house from which a water drop falls.
  • 💧 The water drop starts with an initial velocity of 0 m/s.
  • ⏱ The time taken for the drop to fall is 3 seconds.
  • 📉 The final position of the water drop is the ground level, represented as 0 m.
  • 🌍 The acceleration due to gravity is given as 9.8 m/s², acting downwards.
  • 📝 The script discusses the use of kinematic equations to solve for the initial height.
  • 🔢 The kinematic equation chosen for the scenario is y = y₀ + v₀t + 1/2at².
  • ✂️ The script simplifies the equation by considering the initial velocity (v₀) as 0 and the final position (y) as 0.
  • 🔍 The simplified equation to solve for the initial height (y₀) is y₀ = -1/2at².
  • 📐 The values for gravity (a) and time (t) are substituted into the equation to find y₀.
  • 📈 The calculation results in an initial height of 44.1 meters for the house.
Q & A

  • What is the context of the given transcript?

    -The transcript describes a physics problem involving a water drop falling from the roof of a house, using kinematic equations to calculate the height of the house.

  • What is the initial velocity of the water drop according to the script?

    -The initial velocity of the water drop is given as 0 m/s.

  • How long does it take for the water drop to fall to the ground?

    -The time taken for the water drop to fall is 3 seconds.

  • What is the acceleration due to gravity used in the calculations?

    -The acceleration due to gravity used in the calculations is 9.8 m/s².

  • What are the three kinematic equations mentioned in the script?

    -The three kinematic equations mentioned are V = V₀ + at, v² = v₀² + 2aΔy, and y = y₀ + v₀t + 1/2at².

  • Why is the final position term ignored in the equation?

    -The final position term is ignored because the water drop falls to the ground, which is at position y = 0, making this term zero.

  • How is the initial height of the house calculated in the script?

    -The initial height of the house is calculated by rearranging the kinematic equation to solve for y and substituting the given values for acceleration, time, and initial velocity.

  • What is the formula used to find the initial height of the house?

    -The formula used to find the initial height is y = -1/2 * a * t², where a is the acceleration due to gravity and t is the time taken to fall.

  • What is the calculated height of the house based on the given values?

    -The calculated height of the house is 44.1 meters.

  • Why is the vertical axis referred to as 'y' instead of 'x' in this context?

    -The vertical axis is referred to as 'y' because the problem deals with vertical motion, and 'y' is commonly used to denote vertical displacement in kinematic problems.

  • What is the significance of distinguishing between the vertical and horizontal axes in projectile motion?

    -Distinguishing between the vertical and horizontal axes helps in solving projectile motion problems by simplifying the equations and making it easier to follow standard solution methods.

Outlines
00:00
📏 Calculating the Height of a House from a Falling Water Drop

This paragraph explains a physics problem where a water drop falls from the roof of a house in 3 seconds. The initial velocity of the drop is 0 m/s, and the acceleration due to gravity is 9.8 m/s². The final position is at ground level, which is considered as 0 m. The paragraph uses kinematic equations to solve for the initial height of the house, which is the starting point of the water drop. By setting the initial velocity to zero and the final position to zero, the equation simplifies to y = -1/2 * a * t². Substituting the given values, the calculation results in an initial height (height of the house) of 44.1 meters.

Mindmap
Keywords
💡Water drop
In the context of the video, 'water drop' refers to a small volume of water that falls from the roof of a house. This term is central to the theme as it is the subject of the physics problem discussed in the video. The water drop is used to illustrate the principles of free-fall motion under the influence of gravity.
💡Initial velocity
The 'initial velocity' is the speed at which an object starts moving from a state of rest. In the video, it is stated that the water drop's initial velocity is 0 m/s, which means it begins its fall from rest. This concept is crucial for setting up the physics equations to calculate the height from which the drop falls.
💡Time
The 'time' in the script refers to the duration it takes for the water drop to fall, which is given as 3 seconds. Time is a key variable in kinematic equations and is essential for determining the distance the water drop travels during its fall.
💡Final position
'Final position' denotes the endpoint of the water drop's motion, which is stated to be at ground level (Y = 0 m) in the script. It is a necessary parameter for calculating the initial height from which the drop falls.
💡Acceleration due to gravity
The 'acceleration due to gravity' is the constant rate of change of velocity of an object in free fall, given as 9.8 m/s² in the script. This acceleration is what causes the water drop to increase in speed as it falls, and it is a fundamental concept in the physics of motion.
💡Kinematic equations
The 'kinematic equations' are mathematical formulas used to describe the motion of an object. In the video, three such equations are mentioned: V = V₀ + at, v² = v₀² + 2aΔy, and y = y₀ + v₀t + 1/2at². These equations are used to relate the initial and final conditions of the water drop's fall to calculate the height of the house.
💡Vertical position
'Vertical position' is the term used to describe the height or depth of an object in a vertical direction. In the script, the vertical axis is labeled as 'y' to distinguish it from horizontal motion, and it is the axis along which the water drop falls.
💡Projectile motion
'Projectile motion' refers to the motion of an object thrown into the air, which has both horizontal and vertical components. Although not the main focus of the video, the script mentions it to illustrate the importance of distinguishing between vertical and horizontal axes when solving motion problems.
💡Initial height
The 'initial height' is the starting point from which the water drop falls, and it is the quantity the video aims to calculate. By using the given values and kinematic equations, the script demonstrates how to find this initial height, which is a key part of the physics problem.
💡Calculation
'Calculation' in the script refers to the process of using the kinematic equations and given values to solve for the unknown initial height of the house. The script provides a step-by-step approach to performing this calculation, which is central to understanding the physics concepts being taught.
Highlights

A water drop falls down from the roof of a house in 3 seconds.

Initial velocity of the water drop is 0 m/s.

The time taken for the drop to fall is 3 seconds.

Final position of the drop is at ground level, Y = 0 m.

Acceleration due to gravity is 9.8 m/s^2.

The initial position represents the height of the house.

Three kinematic equations are used to solve the problem.

Equation V = V0 + at is used to find the final velocity.

Equation v^2 = v0^2 + 2aΔy is used to find the height.

Equation y = y0 + v0t + 1/2at^2 is rewritten for vertical motion.

The vertical axis is denoted as y, while x is for horizontal motion.

For vertical motion, the equation simplifies to y = 1/2at^2.

The initial height (y) is isolated to solve for the house's height.

Plugging in values gives the height of the house as 44.1 m.

The calculation involves squaring the time and acceleration values.

The negative sign in the equation is negated due to squaring.

The final calculation multiplies 4.9 m/s^2 by 3 seconds squared.

Transcripts

Browse More Related Video

AP Physics B Kinematics Presentation #35

AP Physics B Kinematics Presentation #38

High School Physics: Free Fall

Physics Lecture - 4 - Calculating Distance Traveled

AP Physics B Kinematics Presentation #32

Win the Prize Projectile Motion Problem

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics CalculationFree FallInitial VelocityAccelerationGravityKinematic EquationsVertical MotionProjectile MotionHeight CalculationEducational Content