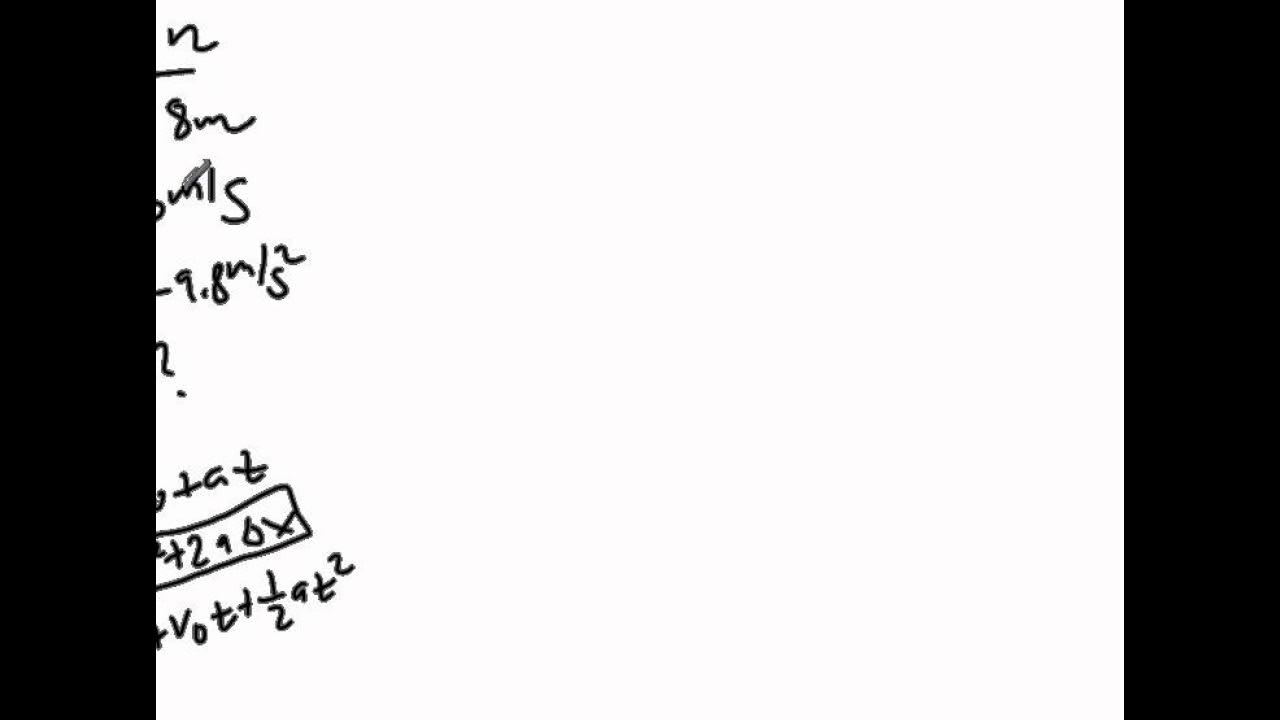Physics Lecture - 4 - Calculating Distance Traveled
TLDRIn this physics tutorial, the presenter explains the concept of acceleration and how to calculate the distance an object, like a tuna can, falls from a building. The key equation discussed is distance traveled (d) = initial velocity (zero in this case) times time (t) plus one-half the acceleration due to gravity (9.8 m/s^2) times time squared. The presenter provides examples for falling distances after 1 second (4.9 meters) and 2 seconds (19.6 meters), and challenges viewers to calculate the distance after 8 seconds for homework.
Takeaways
- 📚 The lesson focuses on understanding acceleration equations, particularly the distance traveled by objects in free fall.
- 🌟 The key formula for calculating distance traveled is: Distance (d) = initial velocity (VO) * time (t) + 0.5 * acceleration (a) * t^2.
- 📈 Acceleration during free fall is consistently 9.8 meters per second squared, which is the acceleration due to gravity.
- 🚫 When the initial velocity is zero (as with the tuna can at the start), the first part of the equation becomes zero, simplifying the formula.
- 🔢 For an object falling for 1 second, the distance traveled is calculated as 0.5 * 9.8 * 1^2, which equals 4.9 meters.
- 🔢 For an object falling for 2 seconds, the distance traveled is calculated as 0.5 * 9.8 * 2^2, which equals 19.6 meters.
- 📐 The distance an object falls increases with the square of the time it has been falling, leading to a rapid increase in distance over time.
- 🥇 The video poses a challenge to calculate the distance a tuna can would fall after 8 seconds, encouraging active participation from viewers.
- 🎓 The lesson emphasizes the importance of understanding the basic principles of physics to solve real-world problems.
- 📝 The homework assignment is to calculate the distance a tuna can falls from the top of a building in 8 seconds, with the first correct answer declared the winner.
- 🎥 The video is educational content aimed at teaching viewers about the principles of acceleration and distance traveled in the context of physics.
Q & A
What is the main topic of the physics tutorial?
-The main topic of the physics tutorial is about acceleration equations, specifically the equation of distance traveled by an object in free fall.
Why is the speed of the falling object constant in the example given?
-In the example given, the speed of the falling object, such as the tuna can, is considered constant because it is under constant acceleration due to gravity, which is 9.8 meters per second squared.
What is the formula for calculating the distance traveled by an object in free fall?
-The formula for calculating the distance traveled by an object in free fall is: d = (v0 * t) + (0.5 * a * t^2), where d is the distance, v0 is the initial velocity, t is the time, and a is the acceleration due to gravity (9.8 m/s^2).
What was the original velocity of the tuna can mentioned in the tutorial?
-The original velocity of the tuna can mentioned in the tutorial was zero, as it was initially at rest in the hands of the person before being dropped.
How far did the tuna can travel after falling for one second?
-After falling for one second, the tuna can traveled a distance of 4.9 meters from the top of the building.
What is the distance traveled by the tuna can after two seconds of falling?
-After two seconds of falling, the tuna can traveled a distance of 19.6 meters from the original point at the top of the building.
What is the significance of the term (0.5 * a * t^2) in the distance formula?
-The term (0.5 * a * t^2) represents the additional distance traveled due to the acceleration of the object over time, which is a result of the constant acceleration caused by gravity.
How does the acceleration due to gravity affect the distance traveled by a falling object?
-The acceleration due to gravity, which is 9.8 m/s^2, affects the distance traveled by a falling object by increasing its speed and consequently the distance covered over time. This is represented in the formula by the term (0.5 * a * t^2).
What homework task was given to the viewers?
-The homework task given to the viewers was to calculate the distance the tuna can would travel after falling for eight seconds from the top of a building.
How can one determine the distance an object will fall in a given time?
-One can determine the distance an object will fall in a given time by using the formula d = (v0 * t) + (0.5 * a * t^2), plugging in the initial velocity, the time of fall, and the acceleration due to gravity.
What is the role of time in the calculation of distance traveled by a falling object?
-Time plays a crucial role in the calculation of the distance traveled by a falling object as it is directly proportional to the distance. The longer the object falls, the more distance it will cover due to the continuous action of gravity.
Outlines
📚 Introduction to Acceleration and Distance Traveled
This paragraph introduces the concept of acceleration and its relationship with distance traveled, specifically focusing on the equation for distance traveled in the context of objects falling under gravity. It explains that acceleration remains constant while speed increases during the fall. The formula for calculating distance is presented as d = VO * t + 0.5 * a * t^2, where VO is the initial velocity, a is the acceleration due to gravity (9.8 m/s^2), and t is the time elapsed. The example of a tuna can falling from a building is used to illustrate the calculation, emphasizing that the initial velocity is zero and thus the first part of the equation equals zero. The calculation is demonstrated for a fall time of one second, resulting in a distance of 4.9 meters.
🧠 Further Examples and Calculation of Distance Traveled
This paragraph continues the discussion on calculating distance traveled by falling objects, using the previously introduced formula. It provides a detailed example of calculating the distance a tuna can falls in two seconds, emphasizing that the original velocity remains zero and the calculation focuses on the acceleration and time components. The result is 19.6 meters, doubling the distance from the one-second example. The paragraph concludes with a homework challenge for the viewers to calculate the distance the tuna can would travel after falling for eight seconds, encouraging engagement and application of the concepts learned.
Mindmap
Keywords
💡acceleration
💡distance traveled
💡original velocity
💡time
💡formula
💡free fall
💡physics tutorial
💡tuna can
💡kinematics
💡homework
Highlights
The lesson focuses on acceleration equations, particularly the equation for distance traveled.
The concept of acceleration staying constant while speed increases is discussed, with an example of a falling tuna can.
The formula for calculating distance traveled is introduced, with 'd' representing distance.
The time variable in the equation represents the time passed since the object began moving.
Acceleration due to gravity is a constant value of 9.8 meters per second squared.
The equation for distance traveled when the original velocity is zero involves the term 1/2 acceleration times time squared.
An example calculation shows that a tuna can falls 4.9 meters in the first second of falling.
In the second example, the tuna can falls 19.6 meters after two seconds.
The original velocity of the tuna can is zero, which simplifies the equation for distance traveled.
The homework challenge is to calculate the distance the tuna can travels after eight seconds.
The video encourages viewers to engage by leaving a comment with their answer to the homework challenge.
The tutorial uses a relatable and humorous example of a falling tuna can to explain the concept of acceleration and distance traveled.
The importance of understanding the relationship between original velocity, time, and acceleration in calculating distance traveled is emphasized.
The lesson is designed to clear up confusion around the equation for distance traveled, especially for objects with an initial velocity of zero.
The tutorial provides a practical application of the physics concepts by using the real-world scenario of a falling object.
The video content is engaging and informative, aiming to make complex physics concepts accessible and understandable.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: