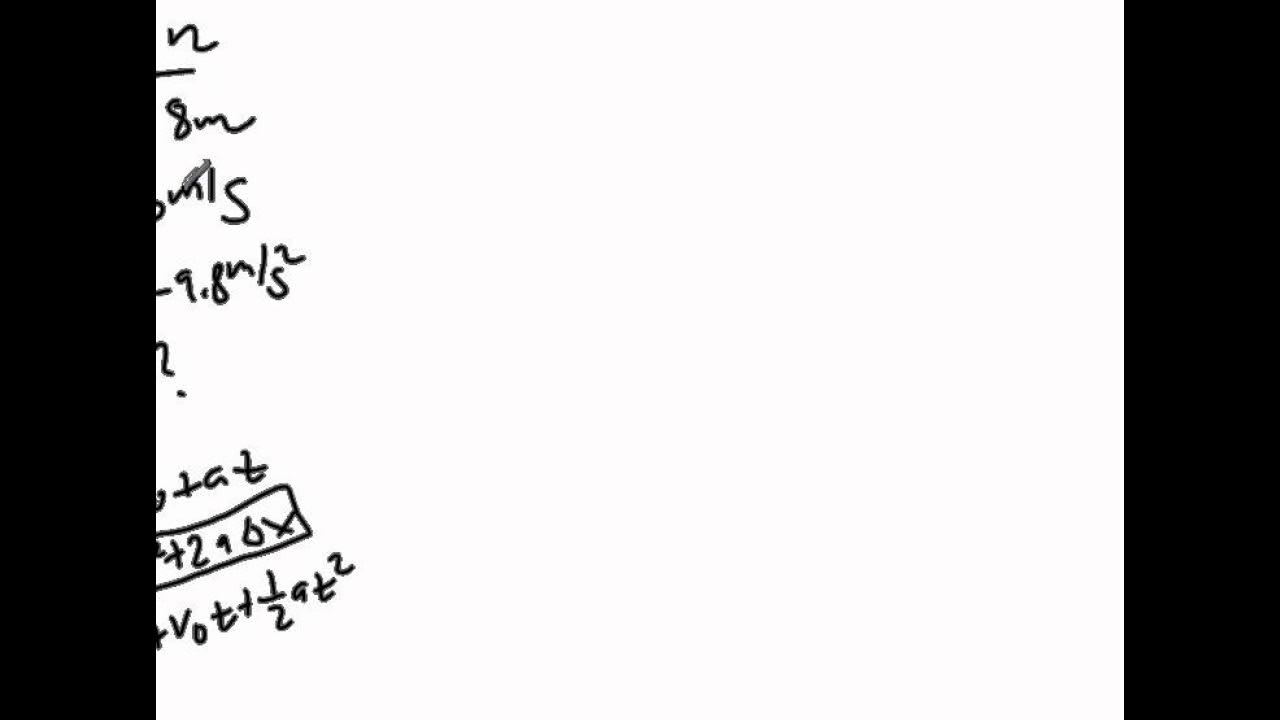AP Physics B Kinematics Presentation #38
TLDRThe video script explains the physics behind a boy throwing a ball vertically upwards and catching it after 3 seconds. It covers the concept of projectile motion, the effect of gravity with an acceleration of 9.8 m/s², and the symmetry of time for ascent and descent. Two methods are presented to calculate the maximum height reached by the ball, resulting in approximately 11 meters. The first method involves solving for initial velocity and using kinematic equations, while the second simplifies the process by focusing on the falling phase and the equation of motion.
Takeaways
- 🏐 The boy throws a ball vertically upwards and catches it after 3 seconds.
- ⏱ The total time for the ball's trajectory is 3 seconds, with equal time for ascent and descent (1.5 seconds each).
- 📉 The acceleration acting on the ball is due to gravity, which is 9.8 m/s².
- 🔍 The initial and final velocities are unknown, requiring inference for calculation.
- 🔑 The first method involves using kinematic equations to solve for the initial velocity and height.
- 🔢 The initial velocity is calculated to be 14.7 m/s using the equation v = v₀ - gt.
- 📈 The height reached by the ball is then calculated using the equation y = v₀t - 1/2gt².
- 📉 The second method simplifies the problem by considering the ball's fall and using the equation y = 1/2gt².
- 📋 Both methods yield a height of approximately 11 meters, rounded to significant figures.
- 📝 The importance of considering significant figures in scientific calculations is highlighted.
- 📚 The script provides a detailed explanation of two methods to solve the problem, emphasizing the process and the thought behind each step.
Q & A
What is the total time of the ball's trajectory described in the script?
-The total time of the ball's trajectory is 3 seconds.
What is the acceleration acting on the ball during its trajectory?
-The acceleration acting on the ball is due to gravity, which is 9.8 m/s².
How is the total time of 3 seconds divided between the ascent and descent of the ball?
-The time up and the time down are the same, each being 1.5 seconds.
What is the initial velocity of the ball when it is thrown upwards?
-The initial velocity is calculated to be 14.7 m/s, which is derived from the time and acceleration.
How is the height the ball reaches calculated in the script?
-The height is calculated using the kinematic equations, considering the initial velocity and acceleration due to gravity.
What is the significance of the initial velocity in solving for the height reached by the ball?
-The initial velocity is crucial as it, along with the time and acceleration, determines the maximum height the ball reaches.
Why are two methods presented for calculating the height reached by the ball?
-Two methods are presented to provide alternative approaches, one being more involved and the other being simpler and more elegant.
What is the height the ball reaches according to the calculations in the script?
-The height the ball reaches is approximately 11 meters, rounded to three significant figures.
Why is the second method considered simpler and more elegant than the first?
-The second method is simpler because it reduces the problem to a single equation involving only acceleration and time, which are known quantities.
How does the script handle the significant figures in the final height calculation?
-The script rounds the height to three significant figures, resulting in 11.0 meters, omitting the trailing zero.
What is the importance of considering both the ascent and descent in the script's explanation?
-Considering both the ascent and descent helps to understand the entire trajectory and provides insights into different aspects of the motion.
Outlines
🚀 Calculating the Maximum Height of a Vertically Thrown Ball
The script begins with a physics problem involving a boy who throws a ball vertically upwards and catches it after 3 seconds. It's established that the total time of the ball's trajectory is 3 seconds, and the acceleration due to gravity is 9.8 m/s². The script explains that the time taken for the ball to ascend and descend is equal, each being 1.5 seconds. The first method to calculate the height involves using the kinematic equations to solve for the initial velocity (14.7 m/s) and then using this to find the height reached by the ball, which is approximately 11 meters. The second method simplifies the process by focusing on the descent, using the same kinematic equations but with the final position set to zero, leading to the same result of 11 meters for the height reached.
📚 Two Methods to Determine the Height Reached by a Thrown Ball
The second paragraph elaborates on two methods to calculate the height a ball reaches when thrown vertically upwards. The first method involves complex calculations using the initial velocity found from the ascent phase, leading to a height of 11 meters. The second method is more straightforward, using the descent phase and simplifying the kinematic equation to solve for height, also resulting in 11 meters. The paragraph emphasizes the importance of understanding both methods, as they provide insight into different aspects of the problem, such as the initial velocity of the throw and the height reached by the ball.
Mindmap
Keywords
💡Vertical throw
💡Trajectory
💡Acceleration due to gravity
💡Projectile motion
💡Time up and time down
💡Initial velocity
💡Kinematic equations
💡Significant figures
💡Apex
💡Height
💡Method
Highlights
A boy throws a ball vertically upwards and catches it after 3 seconds, prompting the question of how high the ball reached.
The entire trajectory of the ball's motion lasts for 3 seconds.
The acceleration acting on the ball is due to gravity, at 9.8 m/s squared.
The time taken for the ball to go up and come back down is the same, each being 1.5 seconds.
Two methods are presented to solve for the height the ball reaches in its trajectory.
The first method involves using the kinematic equations to solve for velocity and height.
The second, simpler method reduces the problem to an equation involving only acceleration and time.
The initial velocity of the ball is calculated to be 14.7 m/s using the first method.
Using the first method, the height reached by the ball is calculated to be approximately 11 meters.
Significant figures are considered in the calculations, rounding the height to 11 meters.
The second method provides a more elegant solution by focusing on the falling part of the trajectory.
By considering the falling part, the equation simplifies to only terms of acceleration and time.
The height reached by the ball is also calculated to be 11 meters using the second method.
Both methods yield the same result, validating the solution.
The problem-solving approach demonstrates the application of physics principles to real-world scenarios.
The transcript provides a step-by-step explanation of the problem-solving process.
The solution to the problem involves understanding projectile motion and the effects of gravity.
The transcript concludes by emphasizing that either method can be used to find the height the ball reaches.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: