AP Physics B Kinematics Presentation #19
TLDRThe script discusses a physics problem involving a car and a delivery truck, both starting from rest and accelerating at the same rate. The car, however, accelerates for twice the time as the truck. Using the first kinematic equation, the final velocity of the car is determined to be twice that of the truck, given that acceleration rates are equal. The problem is solved by setting up equations for both vehicles and simplifying to show the car's velocity is double the truck's, leading to the answer choice C.
Takeaways
- 😀 Both the car and the delivery truck start from rest, with an initial velocity (V₀) of 0 m/s.
- 🚚 The truck and the car accelerate at the same rate, meaning their acceleration (a) is equal.
- 🕒 The car accelerates for twice the amount of time as the truck, denoted as T_car = 2 * T_truck.
- 📚 The first kinematic equation used is V = V₀ + a*t, where V is the final velocity, V₀ is the initial velocity, a is the acceleration, and t is the time.
- 🚗 For the car, the final velocity is calculated using the formula V_car = a * (2 * T_truck).
- 🚚 For the truck, the final velocity is V_truck = a * T_truck, using the same formula with the truck's time.
- 🔍 By comparing the two velocities, it is clear that V_car is twice V_truck because the car accelerates for twice the time.
- 📉 The final speed of the car is twice the final speed of the truck, as derived from the kinematic equations.
- 🎯 The script concludes that the car's final velocity is 2 times the velocity of the truck, which is the answer to the problem.
- 📝 The problem-solving approach involves understanding the given information, applying the kinematic equations, and comparing the results.
- 📑 The transcript is a step-by-step explanation of how to determine the final speed of the car in comparison to the truck.
Q & A
What is the initial velocity of both the car and the delivery truck?
-The initial velocity of both the car and the delivery truck is 0 m/s, as they start from rest.
Are the car and the truck accelerating at the same rate?
-Yes, the car and the truck are accelerating at the same rate, as indicated by 'a of truck is equal to the acceleration of the car'.
How does the acceleration time of the car compare to that of the truck?
-The car accelerates for twice the amount of time as the truck, which is expressed as 'T of car is equal to 2 * the T of the truck'.
What is the formula used to calculate the final velocity of an object undergoing constant acceleration?
-The formula used is V = V₀ + a*t, where V is the final velocity, V₀ is the initial velocity, a is the acceleration, and t is the time.
What is the relationship between the final velocity of the car and the truck, according to the script?
-The final velocity of the car is twice the final velocity of the truck, as derived from the script's explanation.
How does the script describe the process of comparing the final velocities of the car and the truck?
-The script describes the process by setting up the kinematic equation for both the truck and the car, then substituting the relationship between their acceleration times to find that the car's velocity is twice that of the truck's.
What is the final answer to the problem presented in the script?
-The final answer to the problem is that the car's final speed is twice that of the truck, which corresponds to choice C in the script.
Why does the car's final speed end up being twice that of the truck's, even though they accelerate at the same rate?
-The car's final speed is twice that of the truck's because it accelerates for twice the amount of time, resulting in a greater change in velocity.
What assumption is made about the acceleration of the car and the truck in this problem?
-The assumption made is that both the car and the truck have the same constant acceleration throughout the process.
How does the script ensure that the reader understands the relationship between time and velocity in this context?
-The script ensures understanding by explicitly stating the relationship between the car's and truck's acceleration times and then showing how this relationship affects their final velocities.
What kinematic principle is demonstrated in the script's explanation of the car and truck's acceleration?
-The script demonstrates the principle that the final velocity of an object undergoing constant acceleration is directly proportional to the time it accelerates, assuming the same acceleration rate.
Outlines
🚗 Car and Truck Acceleration Problem
This paragraph introduces a physics problem involving a car and a delivery truck, both starting from rest and accelerating at the same rate. The car accelerates for twice the time as the truck. The paragraph outlines the given information: initial velocities are zero, acceleration rates are equal, and the car's acceleration time is twice that of the truck. The goal is to determine the final speed of the car relative to the truck.
📚 Solving the Acceleration Problem
The paragraph explains the process of solving the given acceleration problem using the first kinematic equation, V = V_0 + at. It clarifies that the velocity of the truck is the product of its acceleration and time, and for the car, the velocity is the truck's acceleration times twice the truck's time. The conclusion is that the car's final velocity is twice that of the truck, leading to the answer choice C, which states that the car's speed is much greater than the truck's.
Mindmap
Keywords
💡accelerate
💡rest
💡velocity
💡acceleration
💡time
💡kinematic equation
💡final speed
💡compared to
💡rate
💡meters per second
💡choice
Highlights
Both the car and the delivery truck start from rest and accelerate at the same rate.
The car accelerates for twice the amount of time as the truck.
Initial velocities of both the car and the truck are zero.
The acceleration rate is the same for both the car and the truck.
The final speed of the car is determined by its acceleration and time.
The final speed of the truck is calculated using the first kinematic equation.
The velocity of the truck is the product of its acceleration and time.
The car's velocity formula mirrors that of the truck, with a doubled time factor.
The car's final velocity is twice that of the truck's due to the doubled acceleration time.
Substitution of the car's time as twice the truck's time simplifies the comparison.
The kinematic equations are essential for solving the problem of final velocities.
The problem-solving approach involves comparing the velocities of the car and the truck.
The car's final speed is directly proportional to the truck's final speed, with a factor of 2.
The final answer is derived from the relationship between the car's and truck's velocities.
The solution process is logical and follows the principles of physics.
The problem highlights the application of kinematic equations in real-world scenarios.
The transcript provides a clear step-by-step explanation of the problem-solving process.
Transcripts
Browse More Related Video

AP Physics B Kinematics Presentation #20
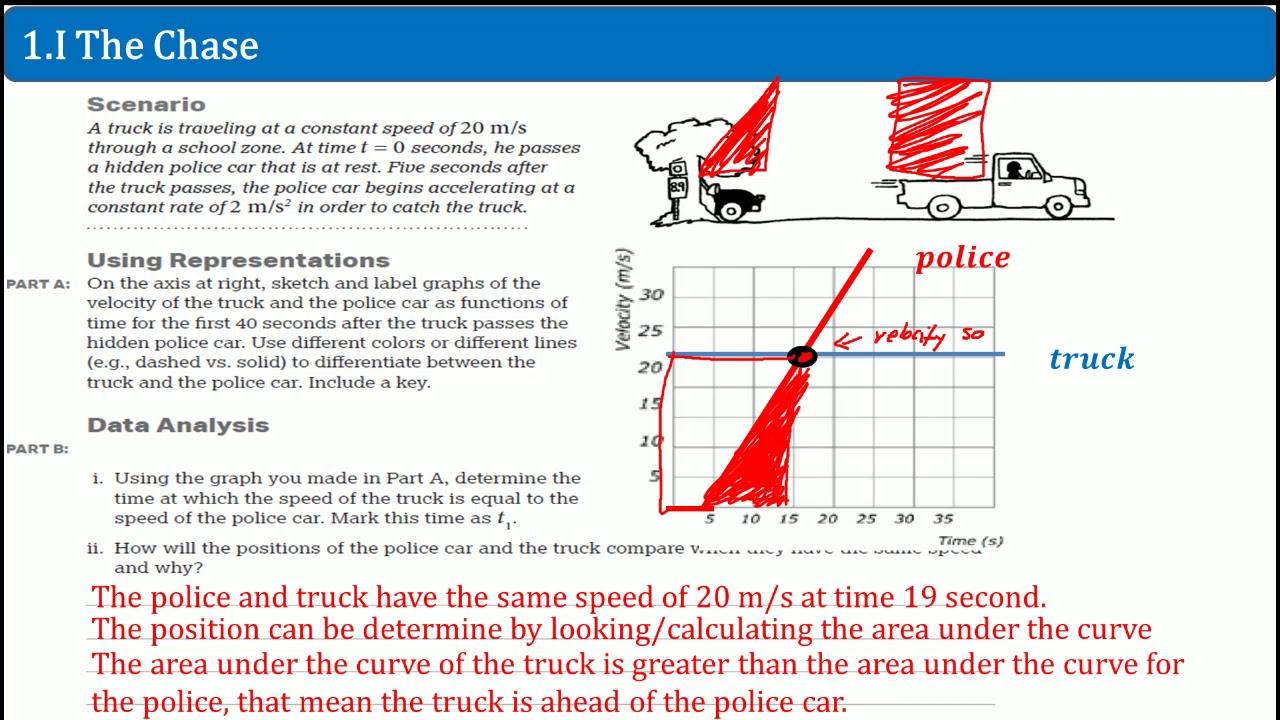
Ap Physics Workbook 1.I The Chase

AP Physics B Kinematics Presentation #21
AP Physics B Kinematics Presentation #18

Related rates: Approaching cars | Applications of derivatives | AP Calculus AB | Khan Academy

AP Physics Workbook 1.H Relationship between Position,Velocity and Acceleration
5.0 / 5 (0 votes)
Thanks for rating: