AP Physics B Kinematics Presentation #21

The New Jersey Center for Teaching and Learning
26 Jun 201205:05
EducationalLearning
32 Likes 10 Comments

TLDRThe script discusses the velocity comparison between a modern car and an antique car, such as a Lanchester, when accelerating over the same distance. It explains that the modern car's acceleration is four times greater. Using the kinematic equation v^2 = u^2 + 2aΞ”x, the script derives the velocity of the antique car and then the modern car, concluding that the modern car's velocity is twice that of the antique car. The explanation is clear, focusing on the relationship between acceleration and velocity without involving time.

Takeaways
  • πŸš— The modern car has an acceleration four times greater than an antique car like the Lanchester.
  • 🏁 Both the modern car and the Lanchester start from an initial velocity of 0 m/s.
  • πŸ”’ The acceleration of the modern car is denoted as \( a_C \) and the antique car as \( a_L \), with \( a_C \) being equal to 4 times \( a_L \).
  • πŸ“ˆ The final velocity of each car is to be compared after they have traveled the same distance, denoted as \( \Delta X \).
  • 🧩 The kinematic equation \( v^2 = u^2 + 2a\Delta X \) is used to relate initial velocity, acceleration, and final velocity.
  • ⏱ Since time is not specified, the kinematic equations involving time are not applicable.
  • πŸ” The equation is manipulated algebraically to solve for the final velocity in terms of \( v \) instead of \( v^2 \).
  • πŸ“š The velocity of the Lanchester, \( V_L \), is derived from the kinematic equation with initial velocity and acceleration.
  • 🚘 The velocity of the modern car, \( V_C \), is calculated using the given relationship between \( a_C \) and \( a_L \).
  • πŸ”— The final velocity of the modern car is found to be twice the velocity of the Lanchester due to the square root of four being two.
  • πŸ“Š The comparison concludes that the modern car's velocity is twice as much as the antique car's velocity after traveling the same distance.
Q & A

  • What is the acceleration of a modern car compared to an antique car like Lanchester?

    -The acceleration of a modern car is four times greater than that of an antique car like Lanchester.

  • What is the initial velocity of both the modern car and the Lanchester?

    -The initial velocity of both the modern car and the Lanchester is 0 m/s.

  • What is the notation used for the acceleration of the modern car and the Lanchester?

    -The acceleration of the modern car is denoted as 'aC' and that of the Lanchester as 'aL'.

  • What is the relationship between the acceleration of the modern car and the Lanchester?

    -The acceleration of the modern car (aC) is equal to four times the acceleration of the Lanchester (4 * aL).

  • What kinematic equation is used to relate velocity, acceleration, and distance traveled?

    -The kinematic equation used is v^2 = u^2 + 2 * a * Ξ”x, where v is the final velocity, u is the initial velocity, a is the acceleration, and Ξ”x is the distance traveled.

  • Why is the equation v^2 = u^2 + 2 * a * Ξ”x preferred for this scenario?

    -This equation is preferred because it includes all the quantities of interest (initial velocity, final velocity, acceleration, and distance) and does not involve time, which is not specified in the problem.

  • How is the final velocity of the Lanchester (VL) calculated?

    -The final velocity of the Lanchester (VL) is calculated using the equation VL = sqrt(2 * aL * Ξ”x), assuming the initial velocity is 0 m/s.

  • What is the relationship between the velocity of the modern car (VC) and the Lanchester (VL)?

    -The velocity of the modern car (VC) is twice the velocity of the Lanchester (VL), as VC = sqrt(4 * 2 * aL * Ξ”x) simplifies to VC = 2 * VL.

  • Why is the square root of four times the velocity of the Lanchester equal to the velocity of the modern car?

    -This is because the modern car's acceleration is four times that of the Lanchester, and when you square root the term '4 * 2 * aL * Ξ”x', the factor of four outside the square root doubles the velocity of the Lanchester to give the modern car's velocity.

  • What insight does the comparison of velocities between the modern car and the Lanchester provide?

    -The comparison shows that with the same distance traveled, a modern car can achieve a significantly higher velocity due to its greater acceleration, highlighting the advancements in automotive technology.

  • How does the script illustrate the application of physics principles to real-world scenarios?

    -The script uses the principles of kinematics to analyze and compare the velocities of two different types of cars, demonstrating how physics can be applied to understand and predict motion in everyday situations.

Outlines
00:00
🏎️ Comparison of Modern and Antique Car Acceleration

This paragraph discusses the acceleration difference between a modern car and an antique car, specifically a Lanchester. It explains that the modern car can accelerate at a rate four times greater than the antique car. The script uses initial velocities of zero for both cars and introduces the accelerations as 'aC' for the modern car and 'aL' for the Lanchester, with 'aC' being four times 'aL'. The main focus is on comparing the final velocities of both cars after covering the same distance, Ξ”X. The kinematic equation v^2 = u^2 + 2aΞ”X is used to derive the velocities, leading to the conclusion that the modern car's velocity is twice that of the Lanchester's, emphasizing the superiority of modern car acceleration.

Mindmap
Keywords
πŸ’‘Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. In the video, it's a key concept used to compare the performance of a modern car to an antique car, such as the Lanchester. The script mentions that a modern car can develop an acceleration four times greater than the antique car, which is a central point in understanding the difference in their velocities over the same distance.
πŸ’‘Antique Car
An antique car refers to a vehicle that is old and often considered a classic or collectible. In the script, the Lanchester is used as an example of an antique car, which is compared with a modern car in terms of acceleration and final velocity over a given distance.
πŸ’‘Modern Car
A modern car represents a vehicle with contemporary design and technology. The video script uses the term to describe a car that can achieve a significantly higher acceleration compared to an antique car, illustrating the advancement in automotive technology.
πŸ’‘Velocity
Velocity is the speed of an object in a specific direction. The script discusses the initial and final velocities of both the antique and modern cars, using it to explain the outcome of their acceleration over a set distance.
πŸ’‘Initial Velocity
Initial velocity is the speed at which an object starts moving from rest. The script specifies that both the modern car and the antique car (Lanchester) have an initial velocity of 0 m/s, which is the starting point for their acceleration.
πŸ’‘Final Velocity
Final velocity is the speed of an object after it has been accelerated. The video's main theme revolves around comparing the final velocities of the modern car and the antique car after they have traveled the same distance.
πŸ’‘Kinematics
Kinematics is a branch of physics that deals with the motion of objects without considering the forces that cause the motion. The script uses kinematic equations to relate the initial and final velocities, acceleration, and distance traveled by the cars.
πŸ’‘Distance (Ξ”X)
In the context of the script, distance refers to the displacement (Ξ”X) over which both cars accelerate from rest. It's a constant value for both vehicles in the comparison and is crucial for the kinematic equation used to determine their velocities.
πŸ’‘Al (Acceleration of Lanchester)
Al represents the acceleration of the antique car, the Lanchester. The script establishes that the modern car's acceleration (AC) is four times that of the Lanchester's (Al), which is essential for calculating the final velocities.
πŸ’‘AC (Acceleration of Car)
AC is the acceleration of the modern car, which is stated to be four times greater than the Lanchester's acceleration (Al). This factor is central to the script's demonstration of how much greater the velocity of the modern car is compared to the antique car.
πŸ’‘Square Root
The square root operation is used in the script to solve for the velocity from the kinematic equation involving the square of the velocity. It's a mathematical tool necessary for manipulating the equation to express velocity in its simplest form.
Highlights

A modern car can develop an acceleration four times greater than an antique car like Lanchester.

The initial velocity of both the modern car and the antique Lanchester is 0 m/s.

The modern car's acceleration, denoted as AC, is four times the acceleration of the Lanchester, denoted as Al (AC = 4 * Al).

The final velocity of the cars is compared after they have traveled the same distance, denoted as Delta X.

The kinematic equation v^2 = u^2 + 2 * a * Delta X is used to relate initial velocity, acceleration, and final velocity.

The equation is rearranged to solve for final velocity: v = sqrt(u^2 + 2 * a * Delta X).

The velocity of the Lanchester (VL) is calculated using its acceleration (Al) and the distance traveled (Delta X).

The velocity of the modern car (VC) is calculated using its four times greater acceleration (4 * Al) and the same distance (Delta X).

The velocity of the modern car is found to be twice the velocity of the Lanchester due to the square root of four being two.

The kinematic equation is chosen for its simplicity and because it does not involve time, unlike other kinematic equations.

The problem setup specifies that both cars start from rest, making the initial velocity zero.

The problem focuses on comparing final velocities after a given distance, rather than at a specific time.

The modern car's higher acceleration results in a significantly higher final velocity compared to the antique car.

The mathematical relationship between acceleration and final velocity is clearly demonstrated.

The problem illustrates the impact of acceleration on the final velocity of a vehicle over a fixed distance.

The solution involves basic algebraic manipulation of the kinematic equation to express final velocity in terms of given quantities.

The comparison of velocities is made possible by expressing both velocities in terms of the Lanchester's acceleration and the distance traveled.

The final result shows a direct mathematical relationship between the velocities of the two cars based on their accelerations.

Transcripts

Browse More Related Video

AP Physics B Kinematics Presentation #19

AP Physics Workbook 1.H Relationship between Position,Velocity and Acceleration

AP Physics B Kinematics Presentation #20

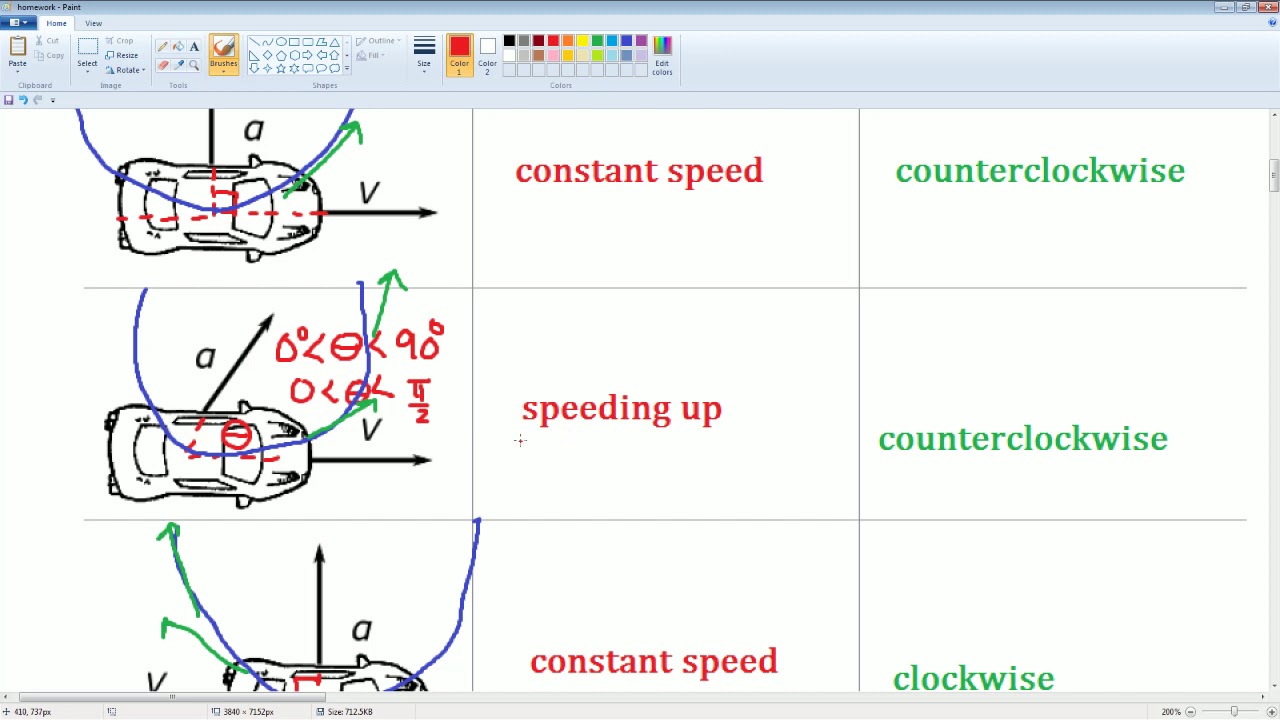
AP Physics Workbook 3.B Direction of Acceleration and Velocity

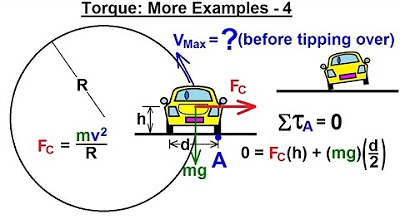
Physics 15 Torque (22 of 25) More Examples: 4 V(max)=? Before Car Tips

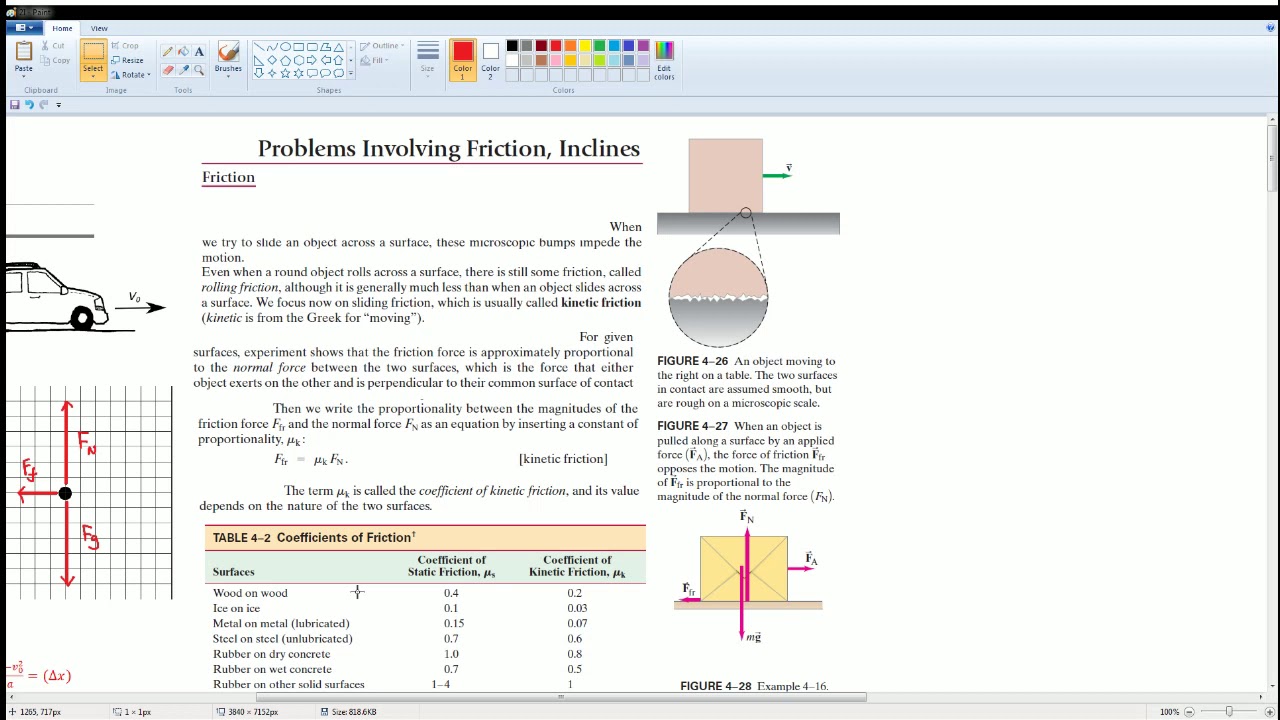
AP Physics Workbook 2.I Stopping Distance

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsAccelerationModern CarsAntique CarsLanchesterKinematicsVelocityCar ComparisonSpeed AnalysisMotion Study