Related rates: Approaching cars | Applications of derivatives | AP Calculus AB | Khan Academy
TLDRThe script presents a mathematical problem involving a car and a truck approaching an intersection, calculating the rate of change of the distance between them. Using the Pythagorean theorem and derivatives, it's determined that the distance is decreasing at a rate of 66 miles per hour as they head towards the intersection.
Takeaways
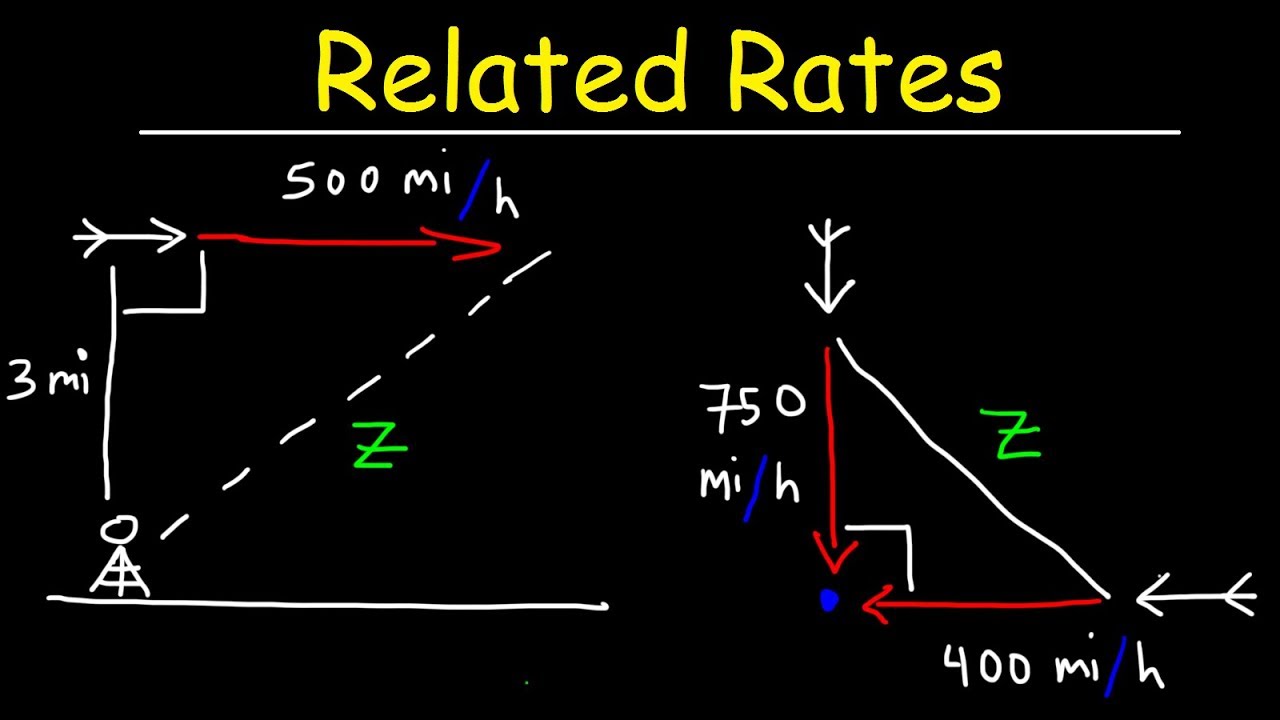
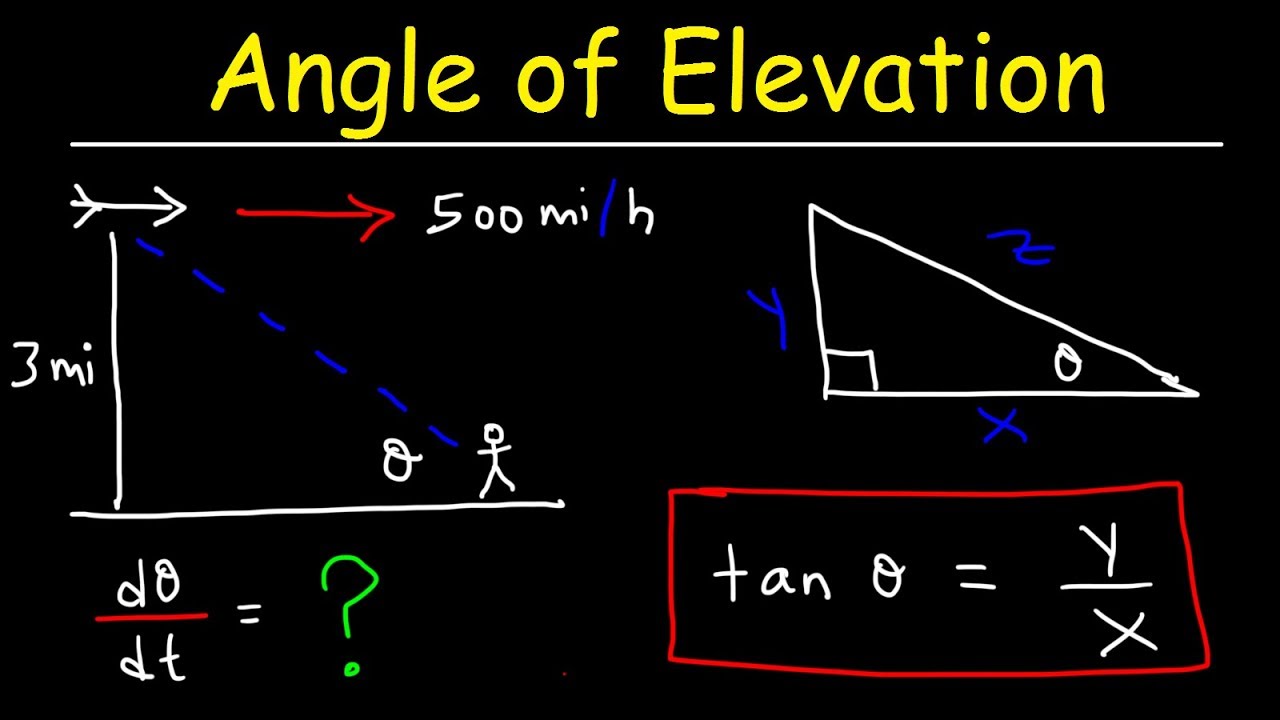
- 🚗 A car is approaching an intersection at a speed of 60 miles per hour and is 0.8 miles away from it.
- 🚚 A truck is approaching the same intersection on a perpendicular street at 30 miles per hour and is 0.6 miles away from it.
- 📐 The relationship between the car, truck, and intersection forms a right triangle, allowing the use of the Pythagorean theorem to calculate distances.
- 🔢 The initial distance between the car and the truck (s) can be found using the Pythagorean theorem: √(0.6^2 + 0.8^2) = 1 mile.
- 📉 The rate of change of distance (ds/dt) is the derivative of the distance with respect to time, which is negative, indicating the distance is decreasing.
- 🎓 To find ds/dt, differentiate the Pythagorean relationship (x^2 + y^2 = s^2) with respect to time, applying the chain rule.
- 🔄 The derivatives of x and y with respect to time are -30 mph and -60 mph, respectively, reflecting their speeds towards the intersection.
- 🧮 The calculation for ds/dt involves substituting the known values into the derived equation: 2x(dx/dt) + 2y(dy/dt) = 2s(ds/dt).
- 📌 After substitution and solving, the rate of change of the distance (ds/dt) is found to be -66 miles per hour.
- 👎 The negative value of ds/dt indicates that the distance between the car and the truck is decreasing at a rate of 66 miles per hour as they approach the intersection.
Q & A
What is the initial distance of the car from the intersection?
-The car is initially 0.8 miles away from the intersection.
How fast is the car approaching the intersection?
-The car is approaching the intersection at a speed of 60 miles per hour.
What is the initial distance of the truck from the intersection?
-The truck is initially 0.6 miles away from the intersection.
How fast is the truck approaching the intersection?
-The truck is approaching the intersection at a speed of 30 miles per hour.
What is the relationship between the distances x, y, and s in this scenario?
-The relationship between the distances x, y, and s is given by the Pythagorean theorem: x^2 + y^2 = s^2.
What is the derivative of x with respect to time?
-The derivative of x with respect to time is -30 miles per hour (dx/dt = -30 mph).
What is the derivative of y with respect to time?
-The derivative of y with respect to time is -60 miles per hour (dy/dt = -60 mph).
What is the value of s at the moment the scenario is described?
-At the moment the scenario is described, s is equal to 1 mile.
What is the rate of change of the distance s with respect to time?
-The rate of change of the distance s with respect to time (ds/dt) is -66 miles per hour.
Why is the rate of change of the distance s negative?
-The rate of change of the distance s is negative because the distance between the car and the truck is decreasing as they approach the intersection.
How can the Pythagorean theorem help in this situation?
-The Pythagorean theorem helps in this situation by allowing us to establish a relationship between the distances x, y, and s, which is essential for calculating the rate of change of the distance between the car and the truck.
Outlines
🚗 Car and Truck Approaching Intersection
This paragraph introduces a scenario where a car and a truck are approaching an intersection from perpendicular streets. The car is 0.8 miles away from the intersection, traveling at 60 miles per hour, while the truck is 0.6 miles away, traveling at 30 miles per hour. The main focus is to determine the rate of change of the distance (ds/dt) between the two vehicles at that moment. The paragraph sets up the problem by defining the variables s (distance between the vehicles), y (distance of the car to the intersection), and x (distance of the truck to the intersection), and suggests using the Pythagorean theorem to establish a relationship between these variables and their rates of change with respect to time.
🧮 Calculating the Rate of Change of Distance
In this paragraph, the calculation of the rate at which the distance between the car and the truck is changing (ds/dt) is detailed. The solution process involves applying the chain rule to differentiate the Pythagorean relationship (x^2 + y^2 = s^2) with respect to time. The paragraph explains the calculation of the derivatives for x^2 and y^2 and how they relate to the rates of change for x and y, which are -30 mph and -60 mph, respectively. The paragraph concludes with the solution, where ds/dt is found to be -66 miles per hour, indicating that the distance between the two vehicles is decreasing at a rate of 66 miles per hour as they approach the intersection.
Mindmap
Keywords
💡intersection
💡miles per hour (mph)
💡distance
💡rate of change
💡Pythagorean theorem
💡derivative
💡right triangle
💡chain rule
💡positive distance
💡negative value
💡perpendicular
Highlights
The car is approaching an intersection at a speed of 60 miles per hour and is 0.8 miles away from it.
The truck is approaching the same intersection on a perpendicular street at 30 miles per hour and is 0.6 miles away from the intersection.
The initial distance between the car and the truck can be represented by the variable s, which is currently 1 mile based on the Pythagorean theorem.
The rate of change of the car's distance from the intersection (dy/dt) is -60 miles per hour, indicating the car is getting closer to the intersection.
The rate of change of the truck's distance from the intersection (dx/dt) is -30 miles per hour, showing the truck is also getting closer to the intersection.
The relationship between x, y, and s is given by the Pythagorean theorem: x^2 + y^2 = s^2.
To find ds/dt, we differentiate the relationship with respect to time, applying the chain rule.
The derivative of x^2 with respect to time is 2x * dx/dt, using the chain rule.
Similarly, the derivative of y^2 with respect to time is 2y * dy/dt, again by the chain rule.
The derivative of s^2 with respect to s gives us 2s * ds/dt.
Substituting the known values into the derived equation, we can solve for ds/dt, the rate of change of the distance between the car and the truck.
The calculation yields a value of -66 miles per hour for ds/dt, indicating that the distance between the car and the truck is decreasing at this rate.
The negative sign in the result makes sense as it reflects the decreasing distance between the two vehicles as they approach the intersection.
The problem-solving approach involves understanding and applying the concepts of calculus, specifically differentiation, to a real-world scenario.
The scenario demonstrates the practical application of the Pythagorean theorem and the chain rule in calculating the rate of change of distances over time.
The solution process highlights the importance of establishing relationships between variables and differentiating these relationships to find the rate of change.
The problem illustrates the intersection of mathematical concepts with physics, specifically kinematics, to solve for motion-related rates.
The step-by-step explanation ensures clarity and understanding, making it an educational and informative example of mathematical problem-solving.
The transcript serves as an example of how to communicate complex mathematical processes in a structured and comprehensible manner.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: