Continuity
TLDRThis educational video delves into the concept of continuity in calculus, explaining that a function is continuous if the limit as x approaches a value equals the function's value at that point. It differentiates between removable and non-removable discontinuities, using visual examples like holes and jumps in a graph. The script also covers how to identify discontinuities in piecewise functions and rational functions, and introduces the Intermediate Value Theorem. Additionally, it touches on the average rate of change, illustrating it with the slope of a secant line and providing examples, including a practical scenario of water being pumped into a tank.
Takeaways
- 📚 The new definition of a continuous function in calculus is that it is continuous at a particular x value if the limit as x approaches that x value is equal to the function's value at that point.
- 📈 The concept of continuity is related to the ability to draw the function's graph without lifting the pencil, indicating no breaks or holes in the graph.
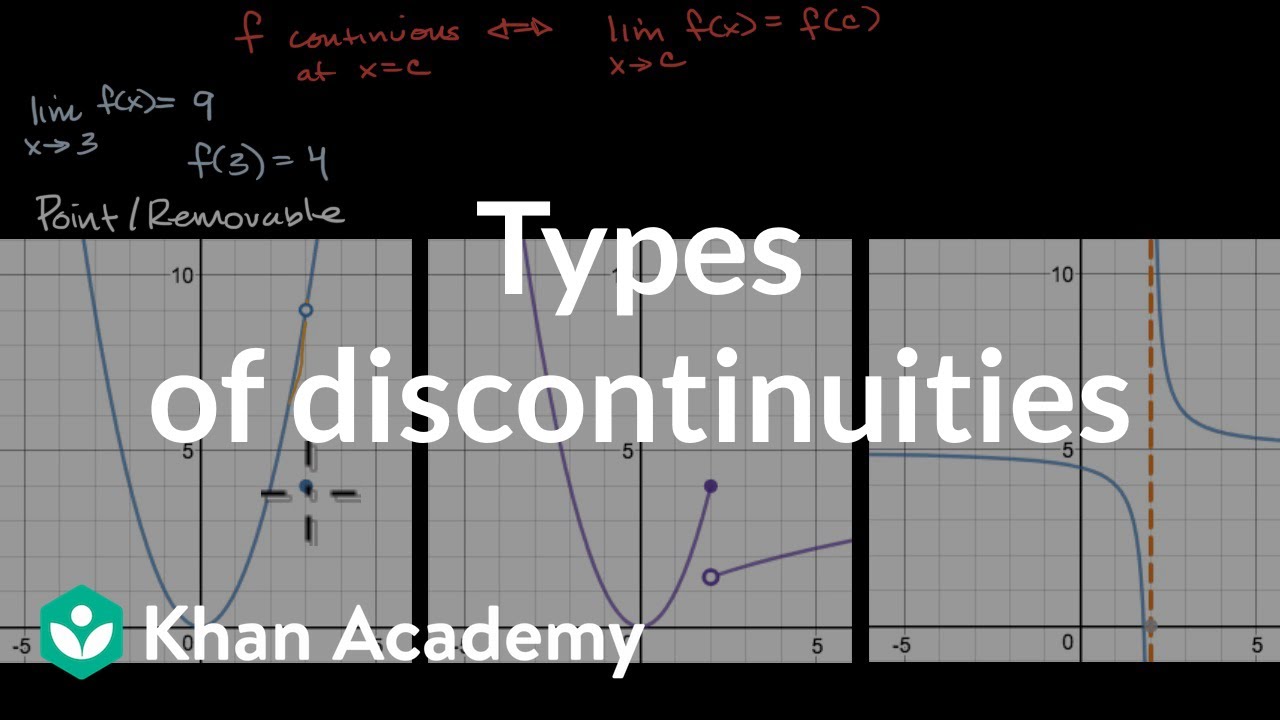
- 🕳️ Removable discontinuities are like holes in the graph where the limit exists but is not equal to the function's value at that point, such as when the function value is undefined.
- 🚫 Non-removable discontinuities occur in scenarios like jump discontinuities and vertical asymptotes where the limit does not exist.
- 🔍 To identify discontinuities in a function, look for points where the function is not defined or where the limit exists but is not equal to the function's value.
- 📉 Functions with redundant factors in the numerator and denominator can have removable discontinuities when factors cancel out, leaving a hole in the graph.
- 🔢 The Intermediate Value Theorem states that if a function is continuous on a closed interval and a value lies between the function's values at the interval's endpoints, then the function must take that value at some point in the interval.
- 📶 The minimum number of x-intercepts a continuous function can have is one, as it must cross any horizontal line between its range values at least once.
- 📌 The average rate of change is calculated as the rise over run, or in function terms, (f(b) - f(a)) / (b - a), representing the slope of the secant line between two points on the graph.
- 💧 Units for the average rate of change are derived from the units of the dependent variable divided by the units of the independent variable, reflecting the change in the dependent variable per unit change in the independent variable.
- 📚 The script provides examples of finding the average rate of change and discusses how to determine values that make a piecewise function continuous, emphasizing the importance of continuity in these calculations.
Q & A
What is the basic definition of a continuous function in calculus?
-In calculus, a function is considered continuous at a particular value of x if the limit as x approaches that value is equal to the value of the function at that point.
What is a removable discontinuity and how can it be identified in a function's graph?
-A removable discontinuity is a 'hole' in the graph of a function where the limit exists but is not equal to the function's value at that point. It can be identified as an otherwise continuous graph with one point removed.
What are the two main types of discontinuities discussed in the script?
-The two main types of discontinuities discussed are removable and non-removable discontinuities. Removable discontinuities have a hole in the graph where the limit exists but is not equal to the function's value. Non-removable discontinuities include jump discontinuities and vertical asymptotes where the limit does not exist.
How can you determine if a function is discontinuous at a specific point?
-You can determine if a function is discontinuous at a specific point by checking if the limit as x approaches that point does not equal the function's value at that point, or if the function is undefined at that point.
What is the Intermediate Value Theorem and what conditions must be met for it to be valid?
-The Intermediate Value Theorem states that if a function is continuous on a closed interval and y0 is a number between f(a) and f(b), then there exists at least one point c in the interval (a, b) such that f(c) = y0. It is valid only if the function f(x) is continuous.
What is the minimum number of x-intercepts a continuous function can have on its graph?
-A continuous function can have at least one x-intercept on its graph, but theoretically, there is no upper limit to the number of x-intercepts it can have.
What is the formula for calculating the average rate of change of a function over a certain interval?
-The formula for calculating the average rate of change of a function f over an interval [a, b] is (f(b) - f(a)) / (b - a), which represents the slope of the secant line between the two points (a, f(a)) and (b, f(b)) on the graph of the function.
What is a secant line and how is it related to the average rate of change?
-A secant line is a straight line that connects two distinct points on the graph of a function. It is related to the average rate of change as the slope of this secant line represents the average rate of change of the function over the interval between those two points.
How can you find the value of a variable that makes a piecewise-defined function continuous at a certain point?
-To find the value of a variable that makes a piecewise-defined function continuous at a certain point, you set the two expressions of the function equal to each other at that point and solve for the variable.
What is the significance of the average rate of change in the context of calculus?
-The average rate of change is significant in calculus as it is a precursor to the concept of the derivative, which measures the instantaneous rate of change of a function at a specific point. It helps in understanding how quantities change with respect to one another.
Outlines
📚 Introduction to Continuity in Functions
The video begins with an introduction to the concept of continuity in functions. The traditional definition is discussed, which involves the ability to draw a function's graph without lifting the pencil. The presenter then introduces a new definition from calculus, stating that a function is continuous at a specific point if the limit as x approaches that point equals the function's value at that point. The concept of discontinuity is also explained, with examples of 'holes' in the graph and undefined function values at certain points. Two types of discontinuities are highlighted: removable and non-removable, with the former being like a point removed from an otherwise continuous graph and the latter involving jumps or vertical asymptotes where the limit does not exist.
🔍 Identifying Discontinuities and Their Types
This section of the video focuses on identifying when a function is discontinuous and classifying the type of discontinuity. Examples are provided, including a function with a vertical asymptote at x = -3 due to division by zero, which is a non-removable discontinuity. Another example is a piecewise function with a removable discontinuity at x = 1, where the function is defined differently on either side of the point. The video also covers rational functions with redundant factors that, when canceled, create a hole in the graph, indicating a removable discontinuity. The presenter emphasizes understanding the visual representation of these discontinuities rather than their mathematical definitions.
📉 Continuity in Piecewise Functions and the Intermediate Value Theorem
The video moves on to discuss continuity in piecewise functions, illustrating how to determine the values of constants that make the function continuous at certain points. An example is given where a quadratic function needs to meet a linear function at x = 2, and algebraic methods are used to find the value of k ensuring continuity. The concept of the intermediate value theorem is introduced as the first existence theorem, stating that if a function is continuous on a closed interval and a value lies between the function's values at the endpoints of the interval, then the function must cross that value. The presenter notes that the theorem is taken as self-evident and not proven within the scope of the class.
📌 Minimum Number of X-Intercepts for Continuous Functions
The presenter explores the minimum number of x-intercepts a continuous function can have, using both graphical and numerical methods. A sketch illustrates that at least three x-intercepts are possible by connecting five points in a minimal way. The concept of sign changes in a table of values is also discussed as evidence of x-intercepts. The video then poses a question regarding the values of b that ensure two solutions to an equation involving a continuous function on a given interval, concluding that b must be less than one to guarantee two solutions.
📈 Average Rate of Change and Its Applications
The final part of the video introduces the concept of the average rate of change, equated to the familiar 'rise over run' from earlier mathematics. The formula for average rate of change is presented as f(b) - f(a) / (b - a), and its interpretation as the slope of a secant line between two points on the graph of y = f(x) is explained. The units of rate of change are discussed, and an example involving the rate of water pumped into a tank is used to demonstrate the calculation of average rate of change with units. The video concludes with a more complex example involving the sine function to practice calculating the average rate of change over a specific interval.
Mindmap
Keywords
💡Continuity
💡Limit
💡Discontinuity
💡Removable Discontinuity
💡Non-Removable Discontinuity
💡Intermediate Value Theorem
💡Average Rate of Change
💡Secant Line
💡Piecewise Function
💡Vertical Asymptote
Highlights
Introduction to the concept of continuity in calculus with a new definition compared to previous courses.
A function is continuous at a particular x value if the limit as x approaches that value equals the function's value at that point.
Explanation of discontinuity with examples of a 'hole' in the graph and undefined function values.
Differentiation between removable and non-removable discontinuities, with descriptions and illustrations.
Removable discontinuities are like holes in an otherwise continuous graph.
Non-removable discontinuities include jump discontinuities and vertical asymptotes where the limit does not exist.
Analysis of a function's discontinuity at x = -3 due to division by zero, resulting in a vertical asymptote.
Example of a piecewise function with a removable discontinuity at x = 1, where the graph has a hole.
Demonstration of how to identify removable discontinuities in rational functions by factoring and canceling.
Discussion of absolute value functions and their behavior at specific points, leading to jump discontinuities.
Solving for the value of 'k' in a piecewise function to ensure continuity at x = 2.
Introduction to the concept of the intermediate value theorem and its conditions for validity.
Explanation of the minimum possible number of x-intercepts for a continuous function.
Method to determine the values of 'a' and 'b' that make a three-piece function continuous using a system of equations.
Application of the intermediate value theorem to guarantee the existence of solutions to an equation within a continuous function.
Introduction to the concept of average rate of change, its formula, and its representation as the slope of a secant line.
Example calculation of the average rate of change for a function defined by an exponential expression.
Explanation of how to find the average rate of change for a sine function over a specific interval.
Transcripts
Browse More Related Video

Continuity!

3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus

Three Types of Discontinuities in Functions

Continuity Basic Introduction, Point, Infinite, & Jump Discontinuity, Removable & Nonremovable
Types of discontinuities | Limits and continuity | AP Calculus AB | Khan Academy

Calculus 1 Lecture 1.4: Continuity of Functions
5.0 / 5 (0 votes)
Thanks for rating: