Find the values a and b that make the function differentiable

Brian McLogan
9 Oct 201706:05
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the instructor discusses the concepts of continuity and differentiability in the context of functions with piecewise definitions. They emphasize the importance of finding the correct values for variables 'a' and 'b' to ensure a function is differentiable, which involves checking continuity at critical points and ensuring the derivatives from both sides are equal. The instructor guides the audience through solving a system of equations derived from these conditions, illustrating the process of elimination to find the values that make the function differentiable. The session also includes a check for understanding and a brief discussion on solving methods, highlighting the common goal of finding the correct derivative values.

Takeaways
  • 📚 The script discusses the importance of understanding how statements are written in the context of differentiability and continuity of functions.
  • 🔍 It emphasizes that for a function to be differentiable, it must first be continuous, and the derivative from the left and right at a point must be the same.
  • 📉 The example provided illustrates the process of checking continuity at a specific point, in this case, at x equals 1.
  • 📝 The script involves setting up an equation to check continuity by equating the expressions from two different parts of a piecewise function at a certain point.
  • 🧩 The process of differentiability involves taking the derivative of each part of the function and ensuring they match at the point of interest, which is x equals 1 in this case.
  • 🔢 The variables a and b are treated as constants within the derivative equations, representing unknown values that need to be determined for the function to be differentiable.
  • ✏️ The script demonstrates solving a system of equations derived from the conditions of continuity and differentiability to find the values of a and b.
  • 🤔 A mistake in the process is acknowledged, and the speaker re-evaluates their work to ensure accuracy, highlighting the importance of careful calculation.
  • 🔄 The method of solving the system of equations is discussed, with the speaker opting for elimination to isolate the variables.
  • 📌 The final values of a and b that make the function differentiable are found to be -3 and 5, respectively.
  • 🤓 The script encourages checking work and understanding different methods of solving systems of equations, such as substitution or elimination.
Q & A

  • What is the main topic discussed in the transcript?

    -The main topic discussed in the transcript is the concept of differentiability in functions, specifically how to determine the values of variables that make a function differentiable.

  • Why is continuity important when discussing differentiability?

    -Continuity is important because a function must be continuous at a point in order to be differentiable there. It ensures that the function has no breaks or jumps at that point.

  • What are the two conditions mentioned for a function to be differentiable at a certain point?

    -The two conditions are that the function must be continuous at that point, and the derivative from the left and right at that point must be the same.

  • What is the significance of the variables a and b in the context of the transcript?

    -In the context of the transcript, a and b are unknown variables that represent constants in the equations. They are used to find the values that make the function differentiable.

  • What mathematical operation is used to check differentiability at a specific point?

    -The mathematical operation used to check differentiability at a specific point is taking the derivative of the function and then evaluating it at that point.

  • What is the process to find the values of a and b that make the function differentiable?

    -The process involves setting up a system of equations by equating the left and right derivatives at the point of interest and solving for the unknowns a and b.

  • What did the speaker do to eliminate the variable b from the system of equations?

    -The speaker used the method of subtracting the equations to eliminate the variable b, which simplifies the system and allows for solving for the other variable.

  • What algebraic method was mentioned for solving a system of equations?

    -The algebraic method mentioned for solving a system of equations is elimination, which involves subtracting one equation from the other to eliminate one of the variables.

  • What was the value of 'a' found by the speaker after solving the system of equations?

    -The value of 'a' found by the speaker after solving the system of equations was -3.

  • What was the value of 'b' found by the speaker after substituting the value of 'a'?

    -After substituting the value of 'a', the speaker found that the value of 'b' was 5.

  • How does the speaker ensure that the work done is correct?

    -The speaker ensures the work is correct by double-checking the calculations and the process used to solve the system of equations.

Outlines
00:00
📚 Understanding Differentiability and Continuity

The first paragraph discusses the concepts of differentiability and continuity in the context of a function involving variables a and b. The speaker aims to clarify the confusion that might arise from the way statements are written. They emphasize the importance of continuity for differentiability, which requires the function to be continuous and the derivatives from the left and right to be equal. The speaker provides an example of a piecewise function and explains the process of finding the values of a and b that make the function differentiable by setting up a system of equations based on continuity and differentiability conditions at x=1. They solve the system to find that a=-3 and b=5, which are the values ensuring the function's differentiability.

05:02
🔍 Reviewing Algebraic Methods for Solving Systems of Equations

In the second paragraph, the speaker reviews different algebraic methods for solving systems of equations, such as elimination and substitution. They recount a previous example where they checked the differentiability of a function and compare it with the current approach. The speaker acknowledges the possibility of making mistakes and encourages double-checking work. They also invite questions from the audience and briefly mention a past exam, suggesting the relevance of the topic to previous assessments.

Mindmap
Keywords
💡Differentiable
Differentiable refers to a function that has a derivative at a given point, meaning it has a well-defined rate of change at that point. In the video, the concept is central as the speaker is discussing the conditions under which a function can be considered differentiable. The script mentions that to be differentiable, a function must be continuous and the derivatives from the left and right must be equal, particularly in the context of piecewise functions.
💡Continuous
Continuity in the context of the video script refers to a function that does not have any breaks or jumps in its graph. It is a prerequisite for a function to be differentiable. The script uses the example of checking continuity at a specific point, x=1, to ensure there are no 'dissections' or points where the function does not meet, which would violate the condition of continuity.
💡Derivative
A derivative in calculus is the measure of how a function changes as its input changes. In the script, the speaker takes the derivative of two expressions to find the rate of change and then equates these to check differentiability at x=1. The derivative is a fundamental concept used to analyze the behavior of functions, especially in determining their differentiability.
💡Piecewise Function
A piecewise function is a function that is defined by multiple pieces, each with its own expression. The script mentions piecewise functions to illustrate a common scenario where differentiability can be an issue if the left and right derivatives are not the same at the points where the pieces meet.
💡Algebra
Algebra is a branch of mathematics that deals with symbols and the rules for manipulating these symbols. It is mentioned in the script in the context of solving systems of equations, which is a common algebraic technique used to find the values of unknowns, such as 'a' and 'b', that make a function differentiable.
💡System of Equations
A system of equations refers to a set of multiple equations that need to be solved simultaneously. In the script, the speaker forms a system of equations based on the conditions for differentiability and continuity, which are then solved using algebraic methods like elimination or substitution.
💡Constants
In the context of the script, constants are values that do not change. The speaker clarifies that while 'a' and 'b' are unknown variables, they represent constants within the equations used to determine differentiability. This distinction is important when taking derivatives and evaluating them at specific points.
💡Elimination
Elimination is a method used to solve systems of equations by adding or subtracting equations to eliminate one variable and solve for the other. The script mentions the use of elimination to solve for 'a' and 'b' by manipulating the system of equations derived from the conditions of differentiability and continuity.
💡Substitution
Substitution is another method for solving systems of equations where one variable is expressed in terms of another and then substituted into the other equation. The script briefly mentions substitution as a potential method to solve the system of equations, although it ultimately uses elimination.
💡Error Checking
Error checking is the process of verifying the correctness of work, which is an important part of problem-solving, especially in mathematics. The speaker in the script encourages double-checking work to ensure there are no mistakes, highlighting the importance of accuracy in mathematical processes.
Highlights

The importance of understanding how statements are written for differentiability.

Differentiability requires continuity and matching derivatives on both sides of a point.

Two variables require two equations to determine differentiability.

Checking continuity at points where the function could potentially be discontinuous.

Setting up an equation for continuity by equating the two sides at the point of interest.

Differentiability involves taking derivatives and evaluating them at the point in question.

Derivatives represent the slope of the tangent line at a point.

The distinction between variables as unknowns and constants in the equations.

Solving a system of equations to find the values of a and b for differentiability.

Using algebraic methods like elimination to solve for the unknowns.

Finding the value of 'a' by manipulating the system of equations.

Determining the value of 'b' using the previously found value of 'a'.

The values that make the function differentiable are -3 and 5.

The necessity of double-checking work to avoid mistakes in solving equations.

Comparing different methods of solving the same system of equations.

The potential for making simple mistakes in algebraic manipulation.

The importance of confidence in mathematical processes and the possibility of making errors.

Transcripts

Browse More Related Video

Smoothing a Piece-wise Function | MIT 18.01SC Single Variable Calculus, Fall 2010

AP Calculus AB: Lesson 2.5 Differentiability

Calculus AB Unit 3 Review: Derivative Rules

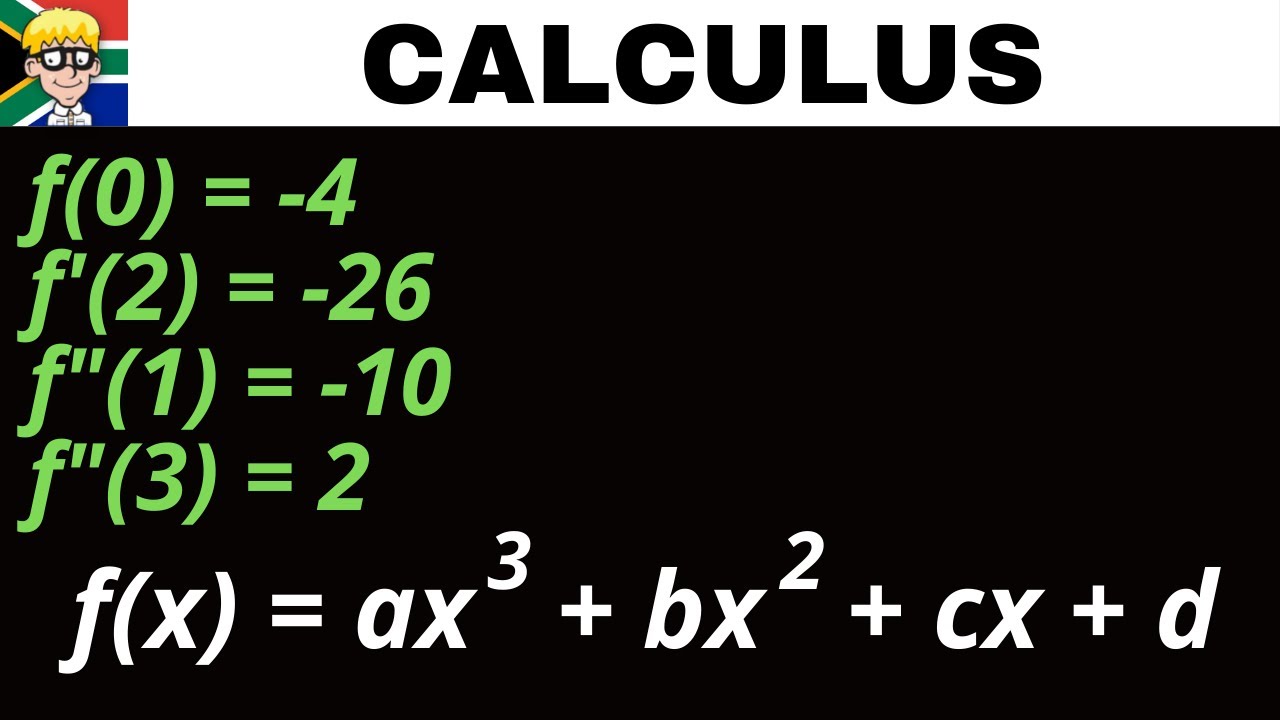
Determine Cubic Equation grade 12

Calculus 1 Lecture 2.1: Introduction to the Derivative of a Function

Finding Intersections of Functions (Precaluclus - College Algebra 22)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DifferentiabilityContinuityAlgebraDerivativesMathematicsEducationalExample AnalysisEquation SolvingVariable ConstantsFunction Analysis