Smoothing a Piece-wise Function | MIT 18.01SC Single Variable Calculus, Fall 2010

MIT OpenCourseWare
7 Jan 201109:15
EducationalLearning
32 Likes 10 Comments

TLDRIn this recitation, Professor Christine Breiner explores the concepts of continuity and differentiability through a piecewise function. She challenges students to determine the values of 'a' and 'b' that ensure the function's continuity and differentiability. The function is defined with a quadratic expression for x > 1 and a linear function for x ≤ 1. The professor illustrates the process of finding the exact point where the linear function must pass to maintain continuity and how the derivative from both sides must match for differentiability. The lesson concludes with identifying the specific 'a' and 'b' values that make the piecewise function both continuous and differentiable, highlighting the importance of matching derivatives for a function to be smooth at a point.

Takeaways
  • 📚 The lecture focuses on the concepts of continuity and differentiability using a piecewise function as an example.
  • 🔍 The function is defined as \( f(x) = x^2 + 1 \) for \( x > 1 \) and as a linear function \( y = ax + b \) for \( x \leq 1 \).
  • 🤔 The task is to find the values of \( a \) and \( b \) that make the function continuous and differentiable.
  • 📈 For continuity, the function must have a linear part that passes through the point (1, 2), which is the value of the function when \( x = 1 \).
  • 📝 The condition for continuity is \( a + b = 2 \), allowing for an infinite number of solutions for \( a \) and \( b \).
  • 📉 To ensure differentiability, the left and right derivatives at \( x = 1 \) must be equal, which means the slope of the left-hand side must match the derivative of the right-hand side function.
  • 🧩 The derivative of the right-hand side function \( x^2 + 1 \) is \( 2x \), and evaluating at \( x = 1 \) gives a derivative of 2.
  • 🔑 The derivative of the left-hand side linear function is \( a \), and for differentiability, \( a \) must equal 2.
  • 📌 The value of \( b \) must be 0 to satisfy both the continuity and differentiability conditions, resulting in the function \( y = 2x \) for \( x \leq 1 \).
  • 📊 The function is continuous for a range of \( a \) and \( b \) values that satisfy \( a + b = 2 \), but only differentiable when \( a = 2 \) and \( b = 0 \).
  • 💡 The piecewise function demonstrates the difference between continuity and differentiability, highlighting that differentiability implies continuity but not vice versa.
Q & A

  • What are the main topics discussed in the recitation?

    -The main topics discussed are continuity and differentiability, with a focus on how a function can be continuous without necessarily being differentiable.

  • What is the function defined in the script?

    -The function is defined piecewise: f(x) = x^2 + 1 when x > 1, and f(x) = a*x + b for a linear function with slope 'a' and y-intercept 'b' when x ≤ 1.

  • What is the significance of the point (1, 2) in the context of the function's continuity?

    -The point (1, 2) is significant because for the function to be continuous, the linear part must pass through this point, ensuring the function's value is consistent as x approaches 1 from both sides.

  • What condition must be met for the function to be continuous?

    -For the function to be continuous, the linear part's equation must satisfy a + b = 2, ensuring the function passes through the point (1, 2).

  • What is the derivative of the function to the right of x = 1?

    -The derivative of the function to the right of x = 1, which is x^2 + 1, is 2x.

  • What is the condition for the function to be differentiable at x = 1?

    -For the function to be differentiable at x = 1, the left-hand derivative (as x approaches 1 from the left) must equal the right-hand derivative (as x approaches 1 from the right), which means a must equal 2.

  • What is the role of the slope 'a' in determining differentiability?

    -The slope 'a' determines the derivative of the linear part of the function. For the function to be differentiable at x = 1, 'a' must be equal to 2, matching the right-hand derivative of the quadratic part.

  • What is the relationship between the values of 'a' and 'b' when the function is differentiable?

    -When the function is differentiable, 'a' must be 2, and 'b' must be 0, to satisfy both the continuity and differentiability conditions, resulting in the linear part being y = 2x.

  • What is the significance of differentiability in comparison to continuity?

    -Differentiability implies a stronger condition than continuity. A function that is differentiable at a point not only has a limit but also has a well-defined derivative, indicating a smooth transition in the function's behavior.

  • Can you provide an example of a function that is continuous but not differentiable?

    -An example from the script is the function with a slope of 1 and a y-intercept of 1 (f(x) = x + 1 for x ≤ 1), which is continuous at x = 1 but not differentiable due to the sharp corner formed.

Outlines
00:00
📚 Introduction to Continuity and Differentiability

Christine Breiner begins the recitation by introducing the topic of continuity and differentiability, explaining that they will explore the difference between a function being continuous and differentiable using a piecewise function as an example. The function is defined such that for x > 1, it equals x squared plus 1, and for x ≤ 1, it is a linear function with a slope 'a' and y-intercept 'b'. The main question posed is to determine the values of 'a' and 'b' that make the function continuous or differentiable. The instructor provides a visual representation of the function for x > 1 and invites students to consider the implications for continuity and differentiability.

05:02
🔍 Analyzing Continuity and Differentiability

The second paragraph delves into the specifics of the continuity and differentiability of the given piecewise function. The instructor explains that for a function to be continuous, the linear part must pass through a specific point determined by the function's value at x = 1, which is (1, 2). This leads to the equation a + b = 2, indicating an infinite number of solutions for 'a' and 'b' that ensure continuity. Several examples are given, such as a constant function and a line with a slope of 1 and y-intercept of 1, noting that these examples are not differentiable at x = 1. The paragraph then transitions to the differentiability question, emphasizing that the derivatives from the left and right must be equal for the function to be differentiable. The derivative of the right side of the function (x > 1) is 2x, and evaluating this at x = 1 gives 2. For the left side (x ≤ 1), the derivative is simply 'a', leading to the conclusion that 'a' must equal 2 for differentiability. The instructor also determines that 'b' must be 0 to satisfy both continuity and differentiability, resulting in a line with a slope of 2 and y-intercept of 0. The summary concludes with a visual representation of how the tangent lines match up perfectly, confirming the function's differentiability.

Mindmap
Keywords
💡Continuity
Continuity in mathematics refers to a property of functions where the limit of the function as the input approaches a certain value is equal to the value of the function at that point. In the context of the video, the concept of continuity is explored through a piecewise function to determine the values of 'a' and 'b' that would make the function continuous at x=1. The script discusses the need for the function to have the same y-value at x=1 from both the left and right sides to ensure continuity.
💡Differentiability
Differentiability is a concept in calculus that indicates a function has a derivative at a certain point, meaning the function's rate of change is well-defined there. The video uses the example of a piecewise function to illustrate how differentiability is a stronger condition than continuity. It requires that the derivatives from the left and right at a point (in this case, x=1) must be equal for the function to be differentiable there.
💡Piecewise Function
A piecewise function is a function that is defined by multiple sub-functions, each applicable to a different interval of the domain. The script introduces a piecewise function where one sub-function is x squared plus 1 for x > 1, and the other is a linear function defined by 'a' and 'b' for x ≤ 1. The exploration of continuity and differentiability in the script is centered around this type of function.
💡Slope
In the context of linear functions, the slope represents the steepness or gradient of the line and is denoted by 'a' in the script. The slope is crucial in determining the linear part of the piecewise function that will be continuous and differentiable at x=1. The script uses the slope to find the relationship between 'a' and 'b' for the function's continuity and differentiability.
💡Y-Intercept
The y-intercept, represented by 'b' in the script, is the point where a linear function crosses the y-axis. It is one of the parameters in the linear part of the piecewise function that the video discusses. The y-intercept, along with the slope, determines the position of the line on the coordinate plane and is essential for the function's continuity at x=1.
💡Limit
In calculus, a limit is the value that a function or sequence approaches as the input approaches a certain value. The video script discusses limits in the context of differentiability, specifically the left and right limits at x=1, to determine if the function has a well-defined derivative at that point. The equality of these limits is necessary for the function to be differentiable.
💡Derivative
The derivative of a function measures the rate at which the function's output changes with respect to its input. The script explains that to be differentiable, the derivative of the function to the right of x=1 (which is 2x) must equal the derivative of the function to the left of x=1 (which is 'a'). The concept is used to find the specific values of 'a' and 'b' that make the function differentiable at x=1.
💡Tangent Line
A tangent line to a curve at a given point is a straight line that touches the curve at that point and has the same slope as the curve at that point. The script mentions tangent lines to illustrate the concept of differentiability, where the tangent lines on either side of x=1 must agree for the function to be differentiable there.
💡Linear Function
A linear function is a function of the form f(x) = ax + b, where 'a' and 'b' are constants, and 'x' is the variable. In the script, the linear function is part of the piecewise function being analyzed for continuity and differentiability. The script explores how choosing specific values for 'a' and 'b' affects the function's properties.
💡Break
In the context of the video, a break refers to a point on a function where there is a sudden change in direction or slope, which can affect continuity and differentiability. The script mentions that a significant break in the function's graph indicates a lack of differentiability at that point.
Highlights

Introduction to the topic of continuity and differentiability using a piecewise function.

The function is defined piecewise with a quadratic part for x > 1 and a linear part for x ≤ 1.

The challenge is to determine values of a (slope) and b (y-intercept) for the linear part to ensure continuity and differentiability.

For continuity, the linear function must pass through the point (1, 2) where the quadratic part is defined.

The y-value at x=1 for the quadratic part is calculated to be 2, setting a condition for the linear part.

An infinite number of solutions for a and b can satisfy the continuity condition, represented by the equation a + b = 2.

Examples of possible lines that satisfy the continuity condition are provided, including f(x) = 2 and f(x) = x + 1.

Differentiability requires the left and right derivatives at x=1 to be equal, leading to a unique solution for a and b.

The derivative of the quadratic part is 2x, and its value at x=1 is 2, setting the condition for the right derivative.

The derivative of the linear part is a, and it must equal 2 to satisfy the differentiability condition.

The value of b must be 0 to ensure both continuity and differentiability when a is 2.

The final function that is both continuous and differentiable is y = 2x for x ≤ 1 and y = x^2 + 1 for x > 1.

The importance of differentiability being a stronger condition than continuity is emphasized.

Graphical representation of the function and its derivatives helps visualize the concept of differentiability.

The function's behavior at the point of transition (x=1) is crucial for both continuity and differentiability.

The significance of the left and right limits of the derivative at the point of transition is explained.

A step-by-step approach to solving for a and b to achieve continuity and differentiability is demonstrated.

The conclusion summarizes the values of a and b that make the piecewise function both continuous and differentiable.

Transcripts

Browse More Related Video

AP Calculus AB: Lesson 2.5 Differentiability

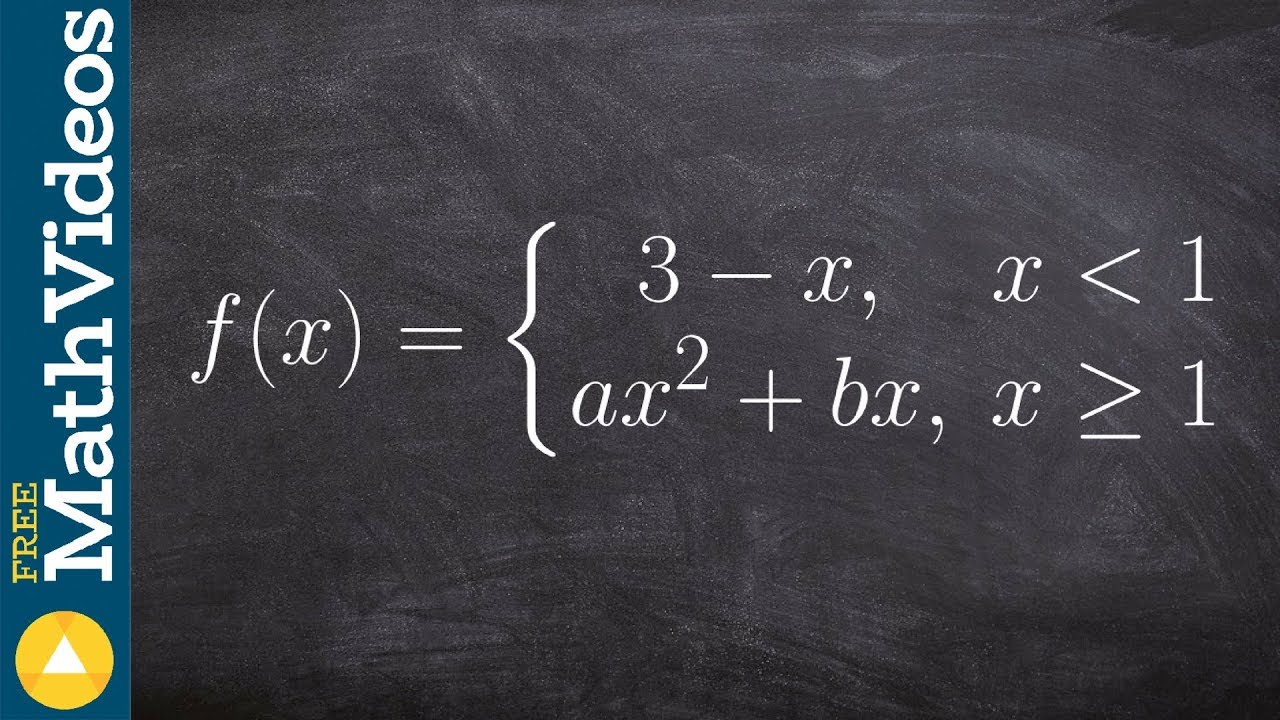
Find the values a and b that make the function differentiable

Differentiability at a point: algebraic (function isn't differentiable) | Khan Academy

BusCalc 16 Continuity and Differentiability

Calculus AB/BC – 1.11 Defining Continuity at a Point

Example: When is a Piecewise Function Continuous?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ContinuityDifferentiabilityPiecewise FunctionMath LectureEducational ContentDerivativeLimitsSlopeY-InterceptFunction AnalysisMathematics Education