Student's T Distribution

365 Data Science
11 Aug 201703:10
EducationalLearning
32 Likes 10 Comments

TLDRWilliam Gosset, known as 'Student', developed statistical methods for selecting the best barley varieties at Guinness. His work on small sample sizes led to the creation of the Student's t-distribution, a significant advancement in statistics for inference with unknown population variance. The t-distribution, with its fatter tails, allows for higher variable dispersion and uncertainty. It's calculated using a formula similar to the z-statistic, considering degrees of freedom, typically n-1. The t-table, like the z-table, is used for inference, becoming similar to the z-table after 30 degrees of freedom, indicating that larger samples approach normal distribution values.

Takeaways
  • 📚 William Gosset, an English statistician at Guinness, developed methods for selecting high-yielding barley varieties.
  • 🔍 Gosset sought efficient ways to make predictions from small samples, as large samples were tedious.
  • 🎭 Due to company policy, Gosset published his work under the pseudonym 'Student'.
  • 📈 Ronald Fisher, Gosset's friend and a renowned statistician, built upon Gosset's work and introduced the t-statistic.
  • 🌟 The Student’s t-distribution is a milestone in statistics, facilitating inference from small samples with unknown variance.
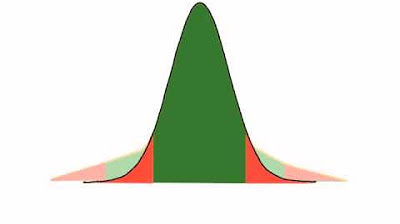
  • 📊 The t-distribution resembles a normal distribution but has fatter tails, indicating greater variability and uncertainty.
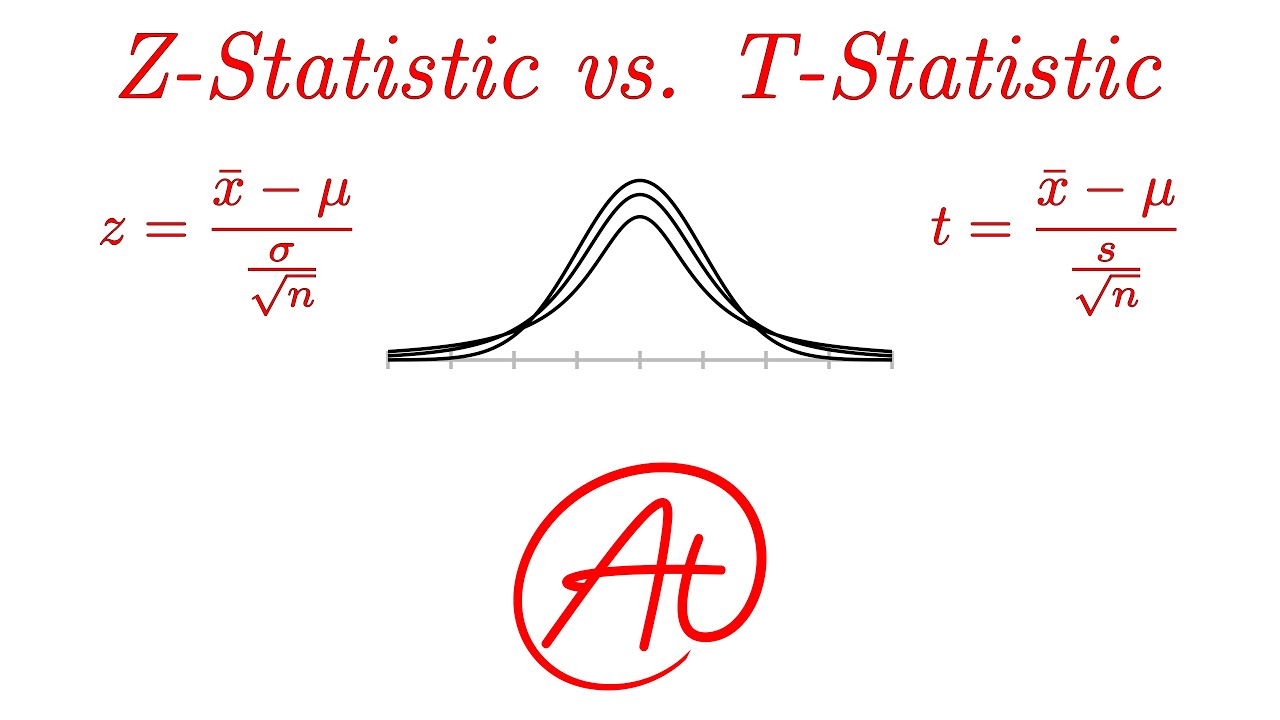
  • 🔢 The t-statistic formula involves the sample mean, population mean, and standard error of the sample, with n-1 degrees of freedom.
  • 📚 The t-statistic is analogous to the z-statistic, serving as an approximation for the normal distribution under certain conditions.
  • 🔑 Degrees of freedom in the t-distribution are typically n-1, where n is the sample size.
  • 📉 The t-distribution table is structured with rows for degrees of freedom and columns for different alpha levels.
  • 🔄 Beyond 30 degrees of freedom, the t-distribution approaches the z-distribution, making the z-table applicable for larger samples.
  • 🚀 The script hints at a forthcoming practical application of the t-distribution in the next lecture.
Q & A

  • Who was William Gosset and what was his professional background?

    -William Gosset was an English statistician who worked for the Guinness brewery. He developed methods for selecting high-yielding barley varieties, which are crucial for beer production.

  • Why did Gosset find big samples tedious and what solution did he develop?

    -Gosset found big samples tedious because they were time-consuming to process. He developed a method to extract small samples that could still provide meaningful statistical predictions.

  • What is the significance of Gosset's work being published under a pen name?

    -Due to the Guinness company policy, Gosset was not allowed to use his real name in publications. All his work was published under the pen name 'Student', which has become synonymous with his contributions to statistics.

  • Who is Ronald Fisher and how did he contribute to Gosset's work?

    -Ronald Fisher was a famous statistician and a friend of Gosset. He built upon Gosset's findings and introduced the t-statistic, which is named after Gosset's pen name, Student.

  • What is the importance of the Student’s t distribution in statistics?

    -The Student’s t distribution is significant because it allows statistical inference through small samples when the population variance is unknown, addressing a common challenge in many statistical problems.

  • How does the Student’s t distribution differ visually from the normal distribution?

    -The Student’s t distribution is similar to the normal distribution but has fatter tails, indicating a higher dispersion of variables due to increased uncertainty.

  • What is the relationship between the t-statistic and the Student’s t distribution?

    -The t-statistic is related to the Student’s t distribution in the same way that the z-statistic is related to the standard normal distribution. It is used for making inferences from sample data.

  • What is the formula for calculating the t-statistic?

    -The t-statistic is calculated with the formula t = (sample mean - population mean) / (standard error of the sample), where the t has n-1 degrees of freedom and a significance level of alpha.

  • What are degrees of freedom and how are they determined in the context of the t-statistic?

    -Degrees of freedom refer to the number of independent values in a set that can vary freely. For a sample of n, the degrees of freedom are n-1, which is used in the calculation of the t-statistic.

  • Why does the t-statistic table become similar to the z-statistic table after a certain point?

    -After 30 degrees of freedom, the t-statistic table becomes almost identical to the z-statistic table because as the sample size increases, the distribution of the sample means approaches a normal distribution.

  • What is the common rule of thumb for when to use the z-table instead of the t-table?

    -A common rule of thumb is to use the z-table instead of the t-table for samples containing more than 50 observations, as the t-distribution becomes more normal with larger sample sizes.

Outlines
00:00
📚 Introduction to William Gosset and the Student's t-distribution

This paragraph introduces William Gosset, an English statistician who worked for Guinness and developed methods for selecting the best barley varieties for beer production. Gosset sought efficient ways to make predictions from small samples, which led to his work under the pseudonym 'Student.' His friend, Ronald Fisher, built upon Gosset's findings and introduced the t-statistic, which is crucial for making inferences from small samples with unknown population variance. The paragraph also explains the visual characteristics of the Student's t-distribution, its relation to the normal distribution, and its significance in statistical analysis.

Mindmap
Keywords
💡William Gosset
William Gosset, also known by his pen name 'Student,' was an English statistician who significantly contributed to the field of statistics with his work on small sample statistics. His research was pivotal in the development of methods that allowed for meaningful predictions based on small samples, which was particularly important in the context of his work with Guinness, where he was tasked with selecting the best barley varieties for beer production. His anonymity was due to the company policy, which is why his work was published under the pseudonym 'Student'.
💡Barley
Barley is an important ingredient in the brewing of beer, as it provides the necessary sugars for fermentation. In the script, Gosset's work with barley is highlighted as an example of how statistical methods can be applied to practical problems in industry. His goal was to find the best yielding varieties of barley, which underscores the relevance of his statistical methods to real-world applications.
💡Small samples
Small samples refer to a limited number of observations or data points collected for statistical analysis. Gosset was interested in developing statistical methods that could provide meaningful predictions even with small sample sizes, which is a significant theme in the video. This is contrasted with larger samples, which can be more tedious to work with but are generally more reliable.
💡Meaningful predictions
Meaningful predictions in the context of the video refer to the ability to make accurate inferences or forecasts based on statistical analysis. Gosset aimed to develop methods that could achieve this with small samples, which is a key concept in the development of the t-distribution and its application in statistics.
💡Ronald Fisher
Ronald Fisher was a famous statistician who built upon Gosset's findings and introduced the t-statistic. Fisher's work is integral to the script's narrative as it highlights the progression of statistical thought and the development of tools that are still in use today, such as the t-distribution.
💡t-statistic
The t-statistic is a statistical measure that is used when the population variance is unknown and the sample size is small. It is named after 'Student,' who was actually William Gosset. The script emphasizes the t-statistic as a breakthrough in statistics, allowing for inference with small samples, which is a fundamental concept in understanding the video's theme.
💡Student’s t distribution
The Student’s t distribution is a type of probability distribution that is used in inferential statistics when the sample size is small and the population standard deviation is unknown. The video explains that this distribution is crucial for statistical inference and has 'fatter tails' than the normal distribution, indicating a higher dispersion of variables.
💡Degrees of freedom
Degrees of freedom in statistics refer to the number of values in the data set that are free to vary. In the context of the t-distribution, the degrees of freedom are typically one less than the number of observations in the sample (n-1). The script uses the concept of degrees of freedom to explain how the t-distribution changes with different sample sizes.
💡Standard error of the sample
The standard error of the sample is a measure of the precision of the sample mean. It is used in the calculation of the t-statistic, as described in the script. Understanding the standard error is important for grasping how the t-statistic is derived and its relation to the sample mean and population mean.
💡Significance level
The significance level, often denoted by alpha (α), is the probability of rejecting the null hypothesis when it is true. In the script, it is used in the context of calculating the t-statistic, where it helps determine the threshold for deciding whether the observed sample mean is significantly different from the population mean.
💡t-table
The t-table is a statistical tool used to find the critical values of the t-distribution for given degrees of freedom and significance levels. The script explains that the t-table is similar to the z-table but is used for smaller sample sizes and unknown population variances. It also notes that after a certain number of degrees of freedom, the t-table values converge with those of the z-table.
Highlights

William Gosset was an English statistician who developed methods for selecting the best yielding varieties of barley for beer production.

Gosset found big samples tedious and sought a way to extract small samples for meaningful predictions.

He published papers under the pen name 'Student' due to Guinness company policy.

Ronald Fisher built upon Gosset's work and introduced the t-statistic, which is still named 'Student’s t'.

Student’s t distribution is a breakthrough in statistics for inference through small samples with unknown population variance.

The t-distribution has fatter tails than the normal distribution, allowing for higher dispersion and more uncertainty.

The t-statistic formula involves degrees of freedom and a significance level, similar to the z-statistic.

The t-statistic is calculated with the sample mean, population mean, and standard error of the sample.

The t-statistic table is used for different degrees of freedom, abbreviated as d.f.

After the 30th row, the t-statistic table values are almost the same as the z-statistic.

For samples with more than 50 observations, the z-table is used instead of the t-table.

The t-distribution is an important part of statistical problems and this course's curriculum.

Gosset's work is still relevant today, contributing to modern statistical methods.

The t-statistic is related to the standard normal distribution, serving as an approximation.

The degrees of freedom for a sample of n are n-1, affecting the t-statistic calculation.

A sample of 20 observations has 19 degrees of freedom, impacting the t-statistic's application.

The upcoming lecture will apply the newly learned knowledge of t-statistics in practice.

Transcripts

Browse More Related Video

Introduction to the t Distribution (non-technical)

Z-statistics vs. T-statistics | Inferential statistics | Probability and Statistics | Khan Academy

t-distribution in Statistics and Probability | Statistics Tutorial #9 | MarinStatsLectures

How to calculate t distributions

Z-Statistics vs. T-Statistics EXPLAINED in 4 Minutes

What is the t-distribution? An extensive guide!

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Statistical MethodsWilliam GossetGuinness BrewerySample SelectionBarley VarietiesStatistical PredictionStudent's TRonald FisherDegrees of FreedomInference TechniquesNormal DistributionT-DistributionZ-StatisticSignificance LevelStandard ErrorSampling TheoryStatistical TablesSmall SamplesPopulation VarianceUncertainty Measurement