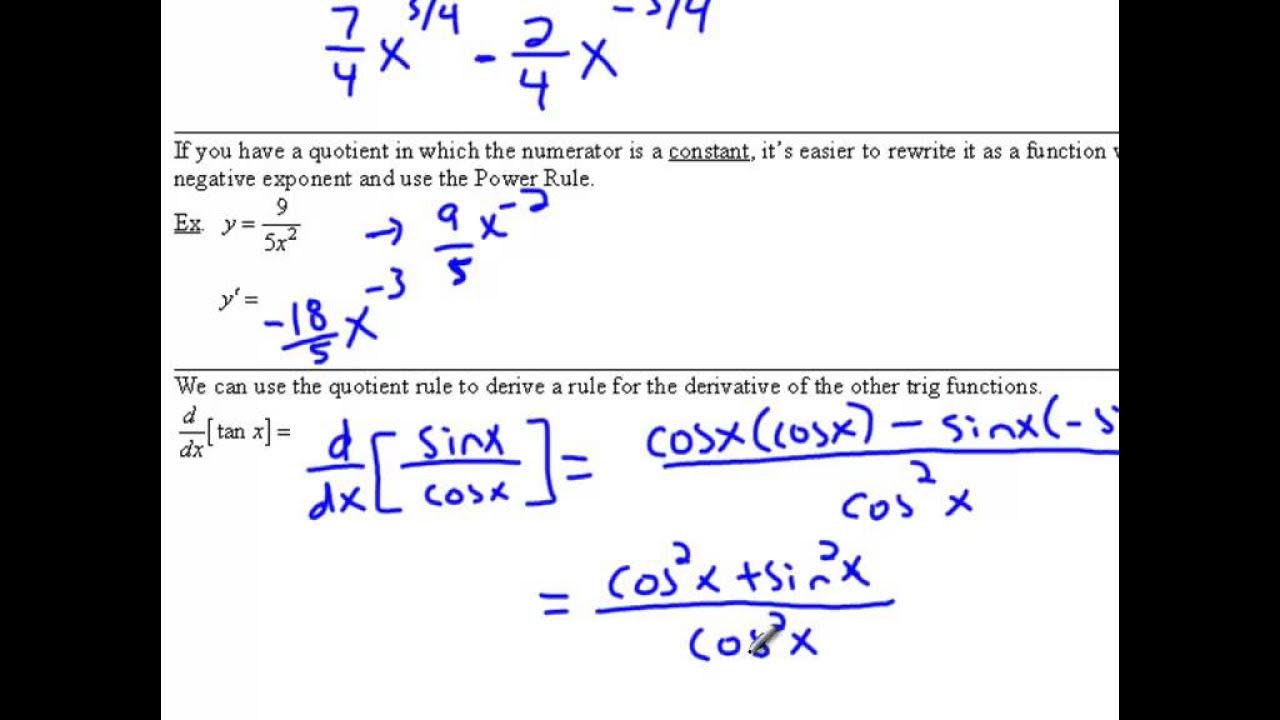The derivative of Trigonometric Functions

Dr. Trefor Bazett
26 Aug 201705:39
EducationalLearning
32 Likes 10 Comments

TLDRIn this video script, the presenter explores the derivatives of the sine and cosine functions without delving into formal geometric proofs. They use a graphical approach to illustrate that the derivative of sine (sin) is equal to cosine (cos) and vice versa, with the derivative of cosine being equal to negative sine. The presenter then applies the quotient rule to find the derivative of tangent (tan), which results in secant squared (sec^2). They emphasize the importance of the Pythagorean identity, cos^2(x) + sin^2(x) = 1, in simplifying trigonometric derivatives. The script also mentions that memorizing these derivatives is crucial for success in calculus due to their frequent use.

Takeaways
  • 📈 The derivative of sine (sin(x)) is equal to cosine (cos(x)).
  • 📉 The derivative of cosine (cos(x)) is equal to negative sine (-sin(x)).
  • 🔶 The tangent function (tan(x)) is defined as sine over cosine (sin(x)/cos(x)).
  • 🔵 The derivative of tangent (tan(x)) is calculated using the quotient rule and results in secant squared (sec^2(x)).
  • 🔸 The Pythagorean identity cos^2(x) + sin^2(x) = 1 is crucial for deriving the derivatives of trigonometric functions.
  • 📌 The derivative of cotangent (cot(x)) can be found by applying the quotient rule to cosine over sine (cos(x)/sin(x)).
  • 📏 The derivative of secant (sec(x)) and cosecant (csc(x)) also follow from the quotient rule and the Pythagorean identity.
  • 🧮 Memorizing the derivatives of trigonometric functions is essential as they are frequently used in calculus.
  • 📚 The provided list of derivatives is lengthy, but understanding the derivatives of sine and cosine is the foundation for the rest.
  • 📝 Practice and repetition are advised for memorizing the derivatives, as they will be used repeatedly in calculus problems.
  • ➗ The derivative of a quotient of two functions is found using the quotient rule, which involves the derivatives of the numerator and denominator.
Q & A

  • What is the derivative of sine with respect to x?

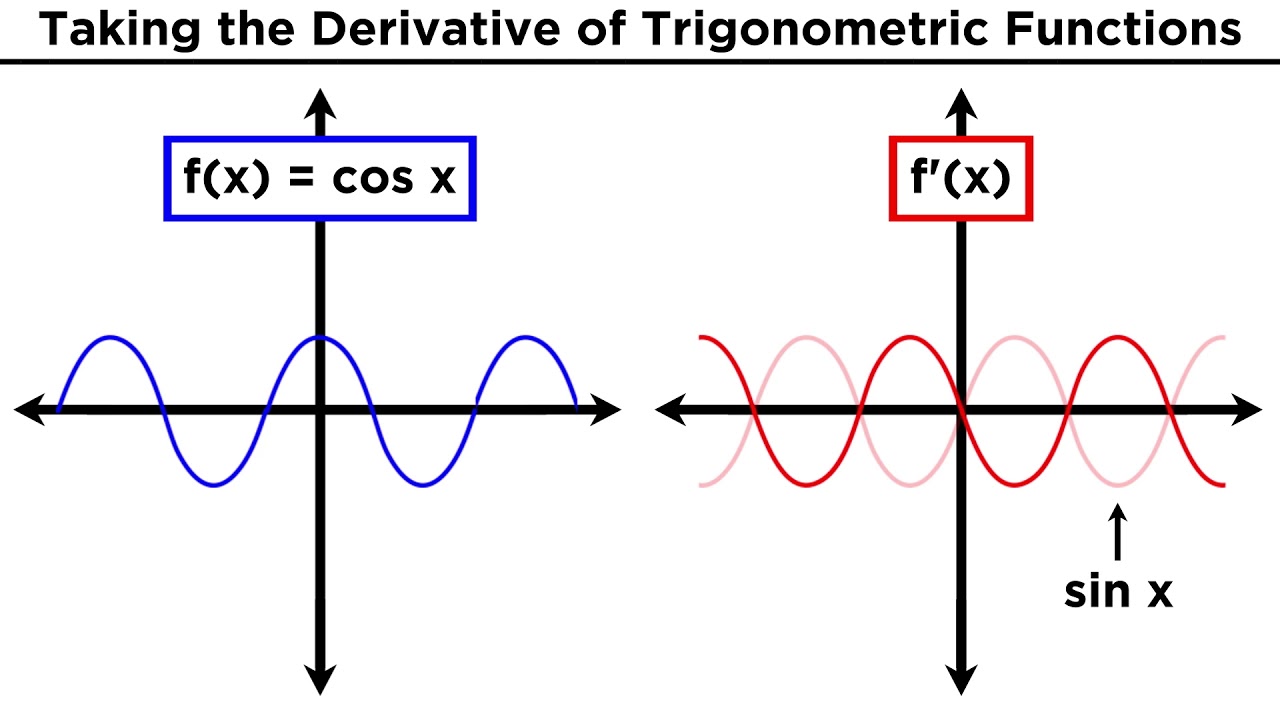
    -The derivative of sine with respect to x is cosine. This is based on the observation that the slope of the tangent line to the sine curve at x=0 matches the value of cosine at that point.

  • What is the derivative of cosine with respect to x?

    -The derivative of cosine with respect to x is negative sine. This is inferred from the fact that as the slope of the tangent line to the cosine curve changes, the value of sine provides the corresponding negative rate of change.

  • How does the value of cosine at x=0 relate to the slope of the tangent line of sine at the same point?

    -At x=0, the value of cosine is 1, and the slope of the tangent line to the sine curve is approximately 1, indicating they are the same at this point.

  • What is the slope of the tangent line to the sine curve at x = π/4?

    -The slope of the tangent line to the sine curve at x = π/4 is less than 1, which corresponds to the value of cosine at π/4, which is 1/√2.

  • At what value of x is the derivative of sine equal to zero?

    -The derivative of sine is equal to zero at x = π/2, which is the point where the sine curve is horizontal.

  • What is the relationship between the derivative of tangent and the quotient rule?

    -The derivative of tangent (tan(x)) is found by applying the quotient rule to the expression sine(x)/cosine(x). The quotient rule states that the derivative of a quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator.

  • What trigonometric identity is used to simplify the derivative of tangent?

    -The Pythagorean identity, which states that cosine^2(x) + sine^2(x) = 1, is used to simplify the derivative of tangent to secant squared of x (sec^2(x)).

  • How can one find the derivative of cotangent using the quotient rule?

    -Since cotangent is defined as cosine/sine, one can find its derivative by applying the quotient rule, considering the derivative of cosine as the negative sine and using the Pythagorean identity to simplify the expression.

  • What is the importance of memorizing the derivatives of trigonometric functions?

    -The derivatives of trigonometric functions are used frequently in calculus, so memorizing them allows for quicker problem-solving and a deeper understanding of the subject.

  • Why does the script mention that only the sine and cosine derivatives need to be memorized?

    -The derivatives of other trigonometric functions can be derived from the sine and cosine derivatives using the quotient rule and the definitions of the respective trigonometric functions.

  • What is the significance of the point x = π/2 in the context of the derivative of cosine?

    -At x = π/2, the derivative of cosine is zero because the cosine curve has a horizontal tangent at this point, and the value of sine at π/2 is zero, which corresponds to the cosine's rate of change being zero.

Outlines
00:00
📈 Derivatives of Sine and Cosine Functions

The first paragraph of the video script discusses the derivatives of the sine and cosine functions without delving into formal geometric proofs. The speaker uses the tangent line at x=0 for the sine function to illustrate that the slope is approximately 1, which aligns with the value of cosine at 0. As the value of x increases, the slope of the tangent line to the sine function decreases, mirroring the decrease in the value of cosine. The speaker concludes that the derivative of sine is equal to cosine and the derivative of cosine is the negative of sine. This understanding is then used to derive the derivatives of other trigonometric functions such as tangent, cotangent, secant, and cosecant by applying the quotient rule and utilizing the Pythagorean identity.

05:02
📚 Memorization of Trigonometric Derivatives

The second paragraph emphasizes the importance of memorizing the derivatives of trigonometric functions, as they are frequently used in calculus. The speaker reassures that while the chart of derivatives may seem long and complicated initially, repeated use will lead to memorization. They highlight that knowing the derivatives of sine and cosine, along with the definitions of other functions like cotangent, is sufficient. The quotient rule can be applied to find the derivatives of these functions during an exam. The speaker encourages practice and repetition to internalize these mathematical relationships.

Mindmap
Keywords
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to a variable. In the context of the video, the speaker is exploring the derivatives of trigonometric functions, specifically sine and cosine, to understand how these functions behave as their input values change. The video uses the tangent line to a graph to illustrate the concept of a derivative, showing how it represents the slope of the function at a particular point.
💡Cosine Function
The cosine function is a fundamental trigonometric function that describes a relationship between the angles and sides of a right triangle. It is represented as cos(x) and is used in the video to derive the derivative of the sine function. The speaker mentions that the value of the cosine function at x=0 is 1, which is a key point in illustrating the relationship between the derivative of sine and the value of cosine.
💡Sine Function
The sine function, like cosine, is a trigonometric function that relates the ratio of the sides of a right triangle to the size of an angle within that triangle. It is denoted as sin(x). The video focuses on finding the derivative of the sine function, which is suggested to be equal to the cosine function through graphical analysis and the observation of the slope of the tangent line to the sine curve at different points.
💡Tangent Line
A tangent line to a curve at a given point is a straight line that 'touches' the curve at that point and has the same slope as the curve at that point. In the video, the tangent line to the sine function at x=0 is used to visually estimate the derivative of sine, which is later confirmed to be cosine through further analysis.
💡Quotient Rule
The quotient rule is a method in calculus for finding the derivative of a function that is the ratio of two other functions. It is used in the video to find the derivative of the tangent function, which is the ratio of the sine function to the cosine function. The rule states that the derivative of a quotient is the denominator times the derivative of the numerator, minus the numerator times the derivative of the denominator, all divided by the square of the denominator.
💡Tangent Function
The tangent function, denoted as tan(x), is another trigonometric function that represents the ratio of the sine to the cosine of an angle. It is used in the video to demonstrate the application of the quotient rule in finding its derivative. The tangent function's derivative is found to be secant squared, which is a result of applying the quotient rule and using the Pythagorean identity.
💡Pythagorean Identity
The Pythagorean identity is a fundamental relationship in trigonometry that states cos²(x) + sin²(x) = 1 for all real numbers x. This identity is crucial in the video as it is used to simplify the expression for the derivative of the tangent function, leading to the result of secant squared.
💡Secant Function
The secant function, written as sec(x), is the reciprocal of the cosine function, or 1/cos(x). It appears in the video as part of the derivative of the tangent function. The speaker uses the secant function to express the final form of the derivative after applying the quotient rule and the Pythagorean identity.
💡Cotangent Function
The cotangent function, abbreviated as cot(x), is the reciprocal of the tangent function, or cos(x)/sin(x). Although not explicitly detailed in the video, it is mentioned as one of the other trigonometric functions whose derivatives can be found using similar methods to those used for sine and cosine.
💡Graph
A graph is a visual representation of the relationship between variables, often used in mathematics to plot the behavior of functions. In the video, the speaker uses graphs of the sine and cosine functions to illustrate their behavior and to deduce their derivatives without going through formal geometric proofs.
💡Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides, particularly in right-angled triangles. In the video, the focus is on the sine and cosine functions, but the speaker also mentions tangent, cotangent, secant, and cosecant as part of the broader family of trigonometric functions, all of which have their own derivatives that can be found using the established rules and identities.
Highlights

The speaker does not go through the formal geometric proof of trigonometric derivatives but aims to illustrate the reasoning behind them.

The derivative of sine at x=0 is approximately 1, matching the value of cosine at the same point.

As x increases, the slope of the tangent line to the sine function decreases, reflecting the decrease in the value of cosine.

The derivative of sine is 0 at x = π/2, where the cosine function also equals 0.

Beyond x = π/2, the slope of the sine function becomes negative, corresponding with the negative values of cosine.

The speaker proposes that the derivative of sine is equal to cosine, based on the observed relationship between their values.

The derivative of cosine is found to be the negative value of sine through a similar analysis.

The derivative of tangent (tan) is derived using the quotient rule and the relationship between sine and cosine.

The Pythagorean identity \( \cos^2(x) + \sin^2(x) = 1 \) is used to simplify the expression for the derivative of tangent.

The final expression for the derivative of tan is \( \sec^2(x) \), where secant is defined as \( 1/\cos(x) \).

The speaker suggests that memorizing the derivatives of trigonometric functions is essential due to their frequent use in calculus.

The derivative formulas for cotangent, secant, and cosecant can be derived using the quotient rule and the Pythagorean identity.

The full list of trigonometric derivatives is provided, which is considered lengthy and complex but necessary to memorize for frequent use.

The importance of practice and repetition in memorizing the derivative formulas is emphasized.

The speaker provides a method to derive the derivative of cosine at x=0, which is horizontal and equals zero.

The value of cosine at π/4 is used to illustrate the change in slope of the tangent line to the sine function.

The concept of the derivative as a measure of the rate of change is applied to understand the behavior of the sine and cosine functions.

The process of deriving the derivative of tangent is explained step by step, emphasizing the use of the quotient rule.

Transcripts

Browse More Related Video

Product and Quotient Rule

Derivatives of Trigonometric Functions

Quotient Rule | MIT 18.01SC Single Variable Calculus, Fall 2010

Lesson 4 - Inverse Hyperbolic Functions (Calculus 2 Tutor)

Derivative of Sine and Cosine Functions | Calculus

Solving Trigonometric Equations By Finding All Solutions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryDerivativesSine FunctionCosine FunctionGraphical AnalysisMath EducationQuotient RulePythagorean IdentityCalculusTrig FunctionsEducational Content