Calculus Chapter 5 Lecture 55 Taylor Series Redux
TLDRIn this calculus lecture, Professor Greist revisits Taylor series, exploring their convergence and the process of turning functions into sequences of coefficients. The lecture delves into the theorem that defines the convergence domain and the properties of differentiable and integrable functions within this domain. It also discusses the practical applications of Taylor series, such as deriving the series for arctan(x) and the Fresnel integrals, and concludes with the concept of real analytic functions, highlighting the distinction between smooth and real analytic functions in the broader universe of mathematical functions.
Takeaways
- 📚 The lecture revisits Taylor series, emphasizing the process of turning a function into a sequence of coefficients and back to a function.
- 🔍 The importance of convergence in Taylor series is discussed, highlighting that it is crucial to understand where the series converges to the original function.
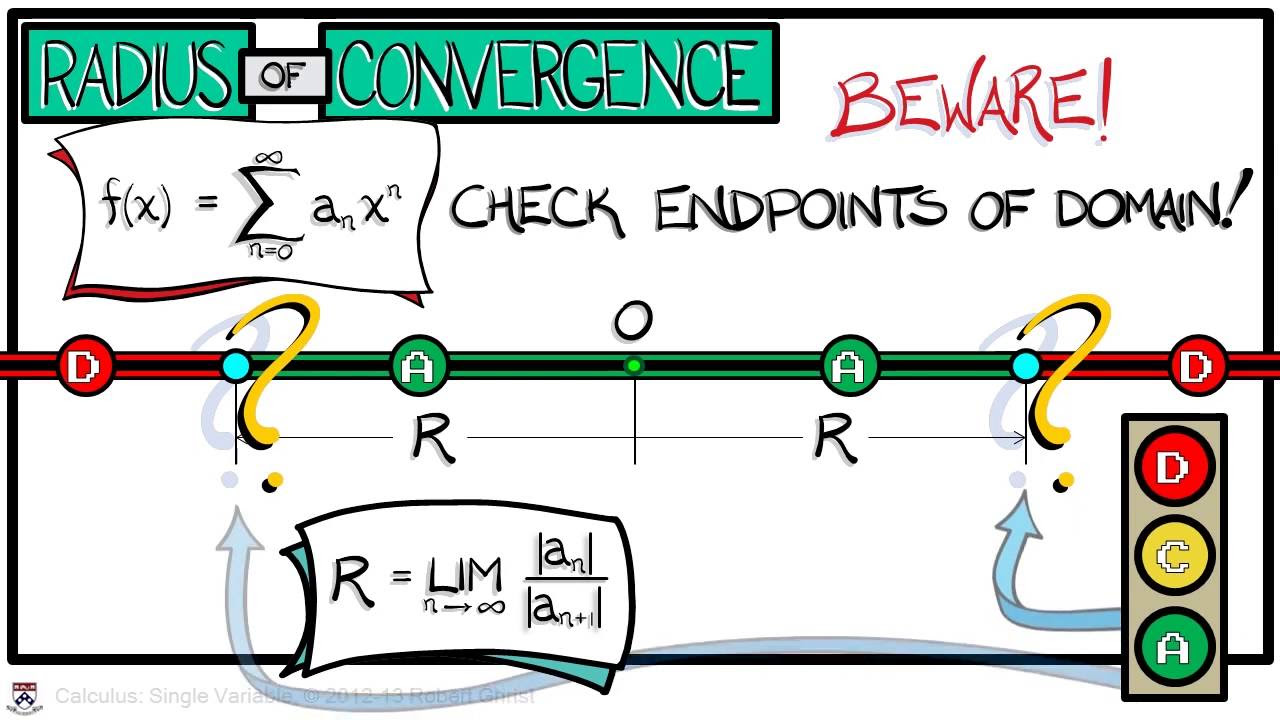
- 📉 The convergence theorem is presented, explaining that a power series converges absolutely within a radius of convergence determined by the ratio of successive coefficients.
- 📈 The role of derivatives in determining the convergence radius is explained, showing that the rate at which derivatives grow affects the series' convergence.
- 📝 The properties of a function within its interval of convergence are detailed, including differentiability and integrability, with derivatives and integrals obtained by term-by-term differentiation and integration of the series.
- 🧭 The practical application of Taylor series is demonstrated through the example of the arctan function, showing how its series can be derived and integrated term by term.
- 🔗 The endpoints of the convergence interval are examined, with the script discussing the conditional convergence of the arctan series at the boundary.
- 🌐 The script explores the geometric series and its derivatives, leading to a deeper understanding of power series and their applications.
- 🔢 The Fresnel integrals are introduced as an example of using Taylor series to define new functions, particularly in optics and diffraction.
- 🤔 The question of ensuring that a Taylor series converges to the original function is addressed, with the necessity of the function being smooth and within the domain of convergence.
- 🌌 The concept of real analytic functions is introduced, explaining that not all smooth functions are analytic, as demonstrated by the example of an exponential function that is not represented by a power series near zero.
Q & A
What is the main topic of Professor Greist's lecture 55?
-The main topic of the lecture is Taylor series, focusing on their convergence and the process of turning functions into sequences of coefficients.
What is the purpose of Taylor expansion in the context of the lecture?
-The purpose of Taylor expansion is to convert a function into a sequence of coefficients, which when reconstituted into a power series, can approximate the original function.
What is the significance of the radius of convergence in the context of power series?
-The radius of convergence, denoted as R, determines the interval within which the power series converges absolutely, and the function is differentiable and integrable within this domain.
How does the lecture define the convergence of a Taylor series about x equals zero?
-The convergence of a Taylor series about x equals zero is defined by the limit of the ratio of the nth coefficient to the (n+1)th coefficient as n approaches infinity.
What property must a function have for its Taylor series to converge to the function itself?
-For a Taylor series to converge to the function itself, the function must be smooth, meaning all derivatives at the point of expansion exist, and the value of x must be within the domain of convergence.
What is a real analytic function according to the lecture?
-A real analytic function is one for which the Taylor series exists and converges to the function for all values of x close to the point of expansion.
How does the lecture illustrate the use of Taylor series in integral calculus?
-The lecture uses the example of the arctan function, showing how its Taylor series can be integrated term by term within the domain of absolute convergence to find the integral of 1/(1+x^2).
What is the geometric series used for in the context of the lecture?
-The geometric series is used to demonstrate the convergence of the arctan function's Taylor series and to show how it can be integrated term by term.
How does the lecture connect the Taylor series to the concept of differentiability?
-The lecture states that within the interval of convergence, not only does the function converge, but it is also differentiable, and the derivative can be obtained by differentiating the series term by term.
What is the significance of the example with the function e^(-1/x) for x > 0 in the lecture?
-The example of the function e^(-1/x) for x > 0 is used to illustrate a function that is smooth but not real analytic, as its Taylor series about x=0 converges to 0, which is not the function for x > 0.
What is the final image or concept presented in the lecture regarding Taylor series?
-The final concept presented is that Taylor expansion can be thought of as a projection to the space of polynomials, where computing a Taylor polynomial is a projection to a finite subspace, effectively discarding higher-order terms.
Outlines
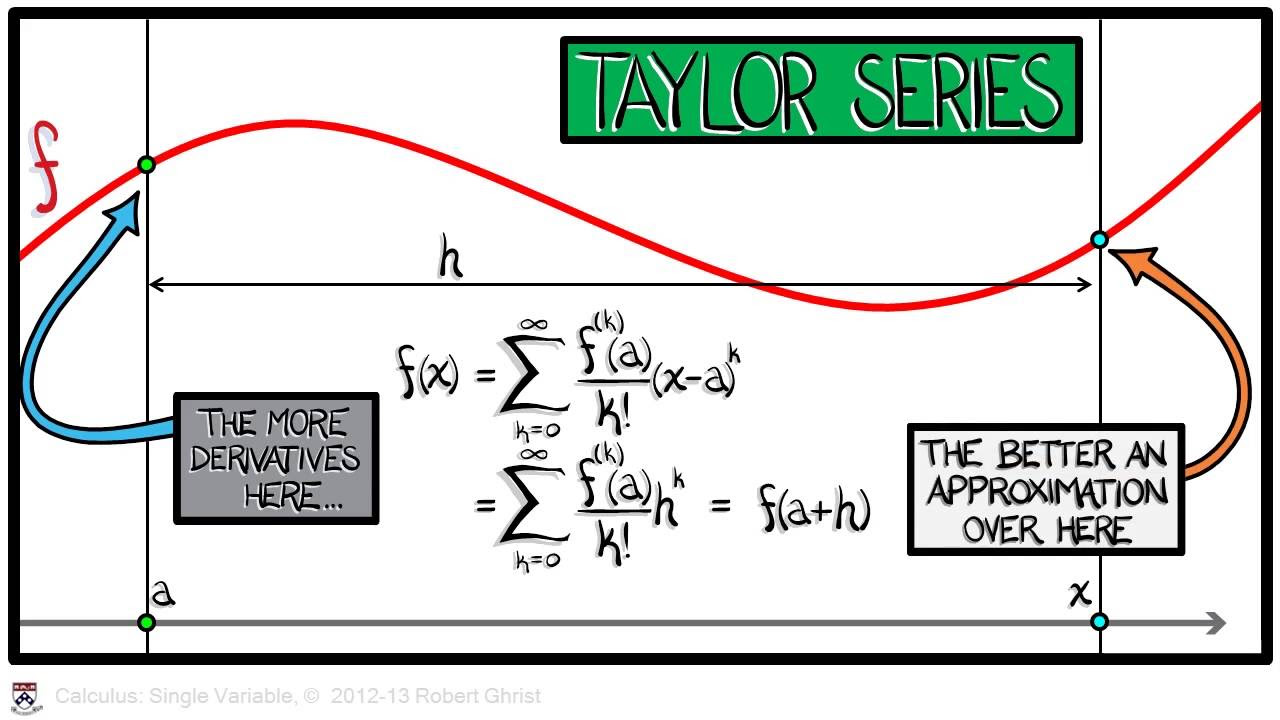
📚 Introduction to Taylor Series Redux
Professor Greist begins Lecture 55 with a metaphorical return to the origins of Taylor series, emphasizing the journey of understanding and the accumulation of knowledge. The lecture revisits power series and the process of converting sequences into functions using Taylor expansion. It highlights the ability to revert this process, starting with a function to derive a sequence of coefficients. The focus then shifts to the convergence of Taylor series, introducing a theorem that defines the radius of convergence and the conditions under which the series converges absolutely. The professor also touches on the differentiability and integrability of functions within the interval of convergence, using the arctan function as an example to demonstrate the application of these concepts.
🔍 Exploring Convergence and Endpoints in Taylor Series
This section delves deeper into the convergence of Taylor series, particularly at the endpoints of the interval of convergence. The professor uses the geometric series to illustrate the behavior of the series at the endpoints, specifically when x equals negative one, leading to an alternating sum that converges conditionally by the alternating series test. The lecture also explores the implications of differentiating and multiplying power series, providing examples of how to evaluate these at specific points, such as x equals 1/10. The Fresnel integrals are introduced as an application of Taylor series in optics, and the challenges of finding antiderivatives for certain functions are discussed, suggesting the use of Taylor series for approximation.
🌐 The Concept of Real Analytic Functions
The third paragraph introduces the concept of real analytic functions, defining them as functions for which the Taylor series exists and converges to the function itself in a neighborhood of a given point. The professor contrasts these with functions that are not real analytic, using an example of a function defined piecewise with an exponential term. The example demonstrates that while the function is smooth, its Taylor series at zero is identically zero, despite the function being positive for x > 0. This leads to a broader discussion about the classification of functions, from polynomials to real analytic functions, and the existence of more complex functions beyond the real analytic category.
🌟 The Role of Taylor Series in Function Analysis
In the final paragraph, the professor synthesizes the understanding of Taylor series, their convergence, and their place within the broader spectrum of functions. Taylor series are likened to a projection onto the space of polynomials, with Taylor polynomials representing a finite projection that discards higher-order terms. The lecture concludes with a preview of the next lesson, which will focus on approximation and error, suggesting a shift from theoretical concepts to more practical applications.
Mindmap
Keywords
💡Taylor Series
💡Power Series
💡Convergence
💡Derivatives
💡Radius of Convergence
💡Differentiable
💡Integrable
💡Arctan Function
💡Geometric Series
💡Real Analytic Function
💡Fresnel Integrals
Highlights
Introduction to Lecture 55 on Taylor series, emphasizing the return to the fundamental concept after exploring various topics.
Explanation of power series and their role in transforming a sequence into a function, f(x).
Inversion of the process from function to sequence using Taylor series, a method already familiar to students.
Taylor expansion as a means to convert a function into a sequence of coefficients that can reconstruct the original function.
Discussion on the coefficients of Taylor series about x=0, involving nth derivatives of f at zero divided by n factorial.
The importance of convergence in Taylor series and the theorem that defines the conditions for absolute convergence.
The relationship between the convergence radius and the rate of growth of the function's derivatives.
Differentiability and integrability of functions within the interval of convergence, and the process of term-by-term differentiation and integration.
The practical application of Taylor series in deriving the series for arctan(x) and its convergence within the interval from -1 to 1.
The endpoint behavior of Taylor series at x = -1, and the conditional convergence demonstrated by the alternating series test.
Differentiation of the geometric series to obtain a simpler power series and its evaluation at specific points.
The surprising simplicity of the decimal expansion resulting from discrete integrals in the context of power series.
The use of Taylor series in defining new functions, such as Fresnel integrals, which are important in optics and diffraction.
The process of obtaining power series formulas for Fresnel integrals by integrating term by term after Taylor expansion.
The question of when a Taylor series converges and the conditions required for a function to be considered real analytic.
The example of a function that is smooth but not real analytic, demonstrating the limitations of Taylor series for certain functions.
The hierarchical structure of functions, starting from polynomials to real analytic functions and beyond.
The final image of Taylor expansion as a projection to the space of polynomials, simplifying the understanding of complex functions.
Anticipation of the next lesson, focusing on approximation and error, bringing the discussion back to more practical problems.
Transcripts
Browse More Related Video

Calculus Chapter 1 Lecture 5 Convergence
Calculus Chapter 1 Lecture 6 Expansion Points
Calculus Chapter 5 Lecture 54 Power Series
When CAN'T Math Be Generalized? | The Limits of Analytic Continuation
The Subtle Reason Taylor Series Work | Smooth vs. Analytic Functions

Calculus Chapter 1 Lecture 3 Taylor Series
5.0 / 5 (0 votes)
Thanks for rating: