Ratio Test -- Radius of Convergence | MIT 18.01SC Single Variable Calculus, Fall 2010
TLDRThis educational video script discusses the application of the ratio test to determine the radius of convergence for various power series. The professor explains the concept using the geometric series as a foundation, then applies the ratio test to several examples, including series for functions like e^x and cosine x. The script clarifies that the radius of convergence can vary, being infinite for some series, and emphasizes the importance of understanding the behavior of series at different values of x.
Takeaways
- 📚 The video script discusses the concept of the radius of convergence for power series and how it relates to the convergence or divergence of series for certain values of x.
- 🔍 The professor clarifies that the radius of convergence can be determined using the ratio test, which involves examining the limit of the ratio of consecutive terms of a series as n approaches infinity.
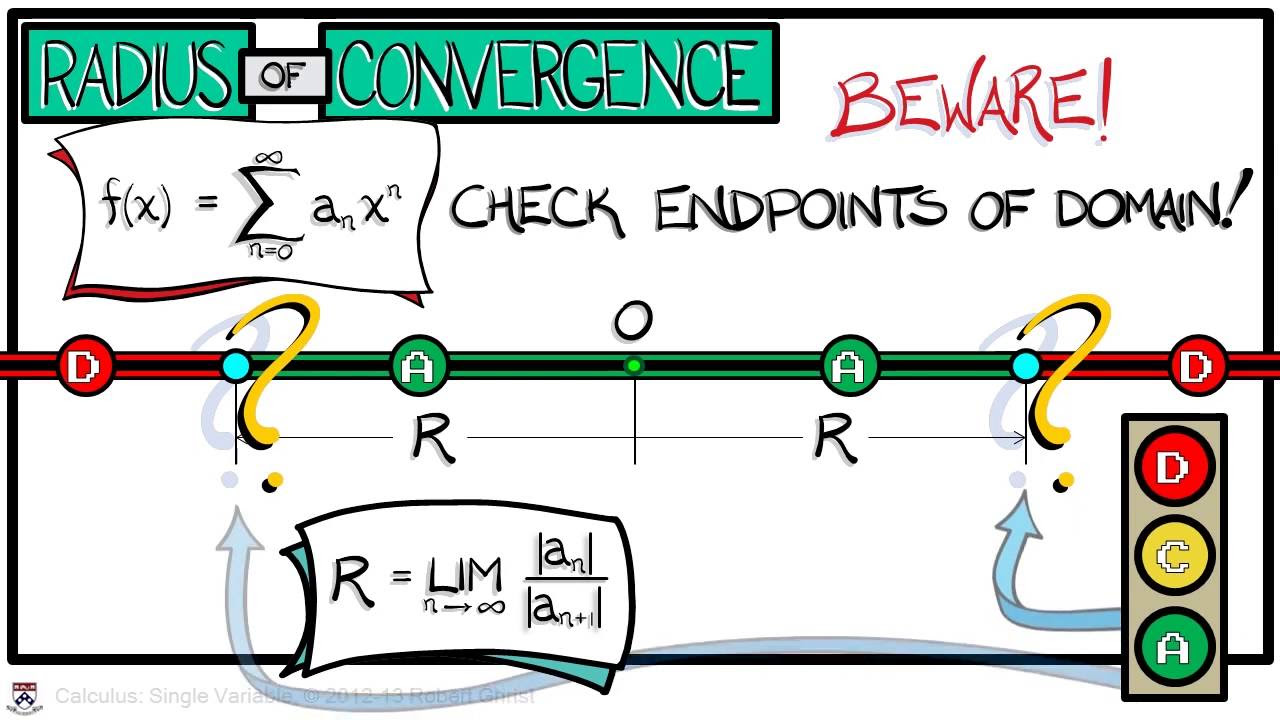
- 📉 The script provides an example of the geometric series \( x^n \) and explains that it converges when the absolute value of x is less than 1 and diverges when it is greater than 1.
- 📐 The concept of 'radius' in the context of convergence is likened to a one-dimensional circle, with the series converging within a certain range of x values centered around zero.
- 🔢 The radius of convergence for a series is numerically determined by solving the inequality derived from setting the limit from the ratio test less than 1.
- 🌐 The script illustrates the process using the series \( \frac{x}{2^n} \), showing that the radius of convergence is 2 by applying the ratio test.
- 📈 Another example given is the series \( \frac{x^n}{n!} \), which is identified as the Taylor series for \( e^x \) and has an infinite radius of convergence.
- 🤔 The importance of considering the absolute value when applying the ratio test is emphasized, as it simplifies the process of determining convergence without needing to consider the sign of x.
- 📝 The script also covers the series \( \frac{x^n}{n \cdot 2^n} \) and demonstrates that the radius of convergence is 2, similar to the previous example but with a different base.
- 🧩 The final examples include series with more complex terms, such as \( \frac{x^{2n}}{(2n)!} \), which is identified as the cosine function and also has an infinite radius of convergence.
- 📚 The video concludes by emphasizing that the ratio test is a powerful tool for determining the radius of convergence and can also provide insights into the behavior of known functions.
Q & A
What is the main topic of the video?
-The main topic of the video is the application of the ratio test to determine the radius of convergence for various power series.
What is the radius of convergence for the series x^n?
-The radius of convergence for the series x^n is 1, as it converges when the absolute value of x is less than 1 and diverges when the absolute value of x is greater than 1.
Why does the professor avoid discussing the case when the absolute value of x equals 1?
-The professor avoids discussing the case when the absolute value of x equals 1 because it is not the focus of the ratio test for determining the radius of convergence in this context.
What is the geometric series and how does it relate to the concept of radius of convergence?
-The geometric series is a series of the form x^n, which converges to 1/(1-x) when the absolute value of x is less than 1. It is used to illustrate the concept of radius of convergence, where the range of x values for which the series converges defines the radius.
How does the ratio test help in finding the radius of convergence for power series?
-The ratio test involves taking the limit of the absolute value of the ratio of consecutive terms of a series as n approaches infinity. If this limit is less than 1, the series converges, and the range of x values for which this condition holds gives the radius of convergence.
What is the radius of convergence for the series x/(2^n)?
-The radius of convergence for the series x/(2^n) is 2, as the series converges when the absolute value of x is less than 2.
What is the significance of taking the absolute value in the ratio test when determining the radius of convergence?
-Taking the absolute value in the ratio test simplifies the process and ensures that the test is sufficient for determining the radius of convergence, regardless of the sign of x.
What is the radius of convergence for the series x^n/n!?
-The radius of convergence for the series x^n/n! is infinite, as the series converges for any value of x due to the limit of the ratio test being 0.
How does the professor use the ratio test to identify the Taylor series for e^x?
-The professor uses the ratio test on the series x^n/n!, which is known to be the Taylor series for e^x, and finds that the limit of the ratio test is 0, indicating an infinite radius of convergence.
What can the ratio test reveal about the convergence of a power series at its endpoints?
-The ratio test can indicate whether a power series converges at its endpoints, but it does not provide definitive information about convergence at these points without further analysis.
Can the ratio test determine the exact values of x for which a power series converges, or only the radius of convergence?
-The ratio test primarily determines the radius of convergence, which is the range of x values within which the series converges. It does not pinpoint the exact values of x for convergence but rather the interval.
What is an example of a power series that has a radius of convergence of 0, and why does this occur?
-A power series might have a radius of convergence of 0 if the limit of the ratio test as n approaches infinity is greater than 1 for all x values. This indicates that the series converges only at x = 0.
Outlines
📚 Introduction to Ratio Test and Radius of Convergence
The professor begins the recitation by revisiting the ratio test, focusing on its application to determine the radius of convergence for power series. The explanation clarifies the concept by referencing a simple geometric series, \( x^n \), and its convergence properties based on the absolute value of x. The series converges for \( |x| < 1 \) and diverges for \( |x| > 1 \). The professor emphasizes the importance of the radius of convergence, which is the range of x values for which the series converges, and introduces the idea of applying the ratio test to other power series to find their convergence radius.
🔍 Applying the Ratio Test to Find Radius of Convergence
The professor demonstrates the application of the ratio test to the power series \( x^n / (2^n) \) to find its radius of convergence. By examining the limit of the ratio of consecutive terms as n approaches infinity, the professor simplifies the expression to \( |x/2| \) and determines that the series converges when \( |x| < 2 \). This example illustrates how the ratio test can be used to find the convergence radius for different power series and reinforces the concept with a geometric series that is known to converge for \( |x| < 1 \).
🌟 Radius of Convergence for e^x and Other Series
The professor explores the radius of convergence for the series \( x^n / n! \), which is the Taylor series for \( e^x \), and explains that it converges for any value of x, indicating an infinite radius of convergence. This is shown by taking the limit of the ratio of consecutive terms, which simplifies to \( x/(n+1) \) and approaches 0 as n goes to infinity. The professor also briefly mentions other series, such as \( x^n / (n \cdot 2^n) \), and how the ratio test can be used to determine their convergence properties.
📉 Analyzing Series with Complex Exponents and Factorials
The professor concludes with an analysis of the series \( x^{2n} / (2n)! \), which is recognized as the Taylor series for the cosine function. The complexity of the factorial terms in the series is addressed, and the professor shows that the limit of the ratio of consecutive terms simplifies to \( x^2 \), indicating that the series converges for all x values, thus having an infinite radius of convergence. The discussion highlights the importance of understanding the behavior of series at their endpoints and the application of the ratio test to various types of series.
Mindmap
Keywords
💡Ratio Test
💡Radius of Convergence
💡Geometric Series
💡Convergence
💡Divergence
💡Power Series
💡Taylor Series
💡Absolute Value
💡Factorials
💡Limit
💡Exponents
Highlights
Introduction to the concept of the radius of convergence in Taylor series.
Explanation of the geometric series convergence for |x| < 1 using the formula 1/(1-x).
Clarification that the radius of convergence is the range of x values for which a series converges.
Illustration of the radius of convergence as a 'circle' on the number line for x values.
Application of the ratio test to determine the radius of convergence for power series.
Use of absolute values in the ratio test for simplicity and convergence determination.
Example calculation using the series x/2^n to demonstrate the ratio test.
Determination that the radius of convergence for x/2^n is 2 based on the ratio test.
Connection between the geometric series and the series x/2^n in terms of convergence criteria.
Application of the ratio test to the series x^n/n! to show its convergence for all x.
Identification of the series x^n/n! as the Taylor series for e^x with an infinite radius of convergence.
Demonstration of the ratio test for the series x^n/(n*2^n) and its convergence for |x| < 2.
Discussion of the possibility of the radius of convergence being zero or only at x=0.
Use of the ratio test for the series x^(2n)/(2n)! to show its convergence for all x.
Identification of the series x^(2n)/(2n)! as the Taylor series for cos(x) with an infinite radius of convergence.
Explanation of the importance of the ratio test in determining the radius of convergence for various power series.
Highlight of the practical use of the ratio test in understanding the behavior of Taylor series for known functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: