Interval and Radius of Convergence

RH Mathematics
20 Feb 202413:39
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video explores the concept of interval and radius of convergence for power series, using the ratio test to determine the values of X that ensure absolute convergence. It demonstrates the process of applying the ratio test, simplifying expressions, and analyzing the behavior of series at endpoints. The video also covers determining the radius of convergence and provides examples to illustrate the concepts, emphasizing the importance of these calculations in understanding the convergence properties of power series.

Takeaways
  • 📚 The video discusses the concept of interval and radius of convergence for power series, which is an extension of the ratio test.
  • 🔍 The ratio test is used to determine the values of 'x' that make a power series converge absolutely by examining the limit of the ratio of consecutive terms.
  • 📉 To apply the ratio test, one must take the limit of the absolute value of the ratio of the (n+1)th term to the nth term of the series.
  • 🌐 The interior of the interval of convergence is found by setting the limit from the ratio test less than one and solving the resulting inequality.
  • 📊 The radius of convergence is determined by measuring the distance from the center of the series (usually x=0) to the endpoints of the interval of convergence.
  • 📌 The video provides an example of finding the interval and radius of convergence for a specific power series, resulting in an interval of (-3, 3).
  • ❗ The endpoints of the interval of convergence require additional tests beyond the ratio test to determine convergence or divergence.
  • 🔄 The process involves checking the behavior of the series at the endpoints by plugging in the specific x values and analyzing the resulting series.
  • 📝 The video emphasizes the importance of understanding intervals of convergence for power series, as they are frequently tested in calculus exams.
  • 🔑 The ratio test is not only useful for finding the interior of the interval of convergence but also for determining the radius of convergence.
  • 📈 The video concludes with additional examples to illustrate the process of finding the radius of convergence with different pieces of information provided.
Q & A

  • What is the main topic discussed in the video?

    -The main topic discussed in the video is the interval and radius of convergence for power series, focusing on the application of the ratio test to determine these properties.

  • What is the ratio test and how is it used in the context of power series?

    -The ratio test is a method used to determine the convergence of a series. It states that a series converges absolutely if the limit of the ratio of consecutive terms goes to a number less than one. In the context of power series, the ratio test is applied by taking the limit of the ratio of the (n+1)th term to the nth term as n approaches infinity, and setting this limit less than one to find the interval of convergence.

  • What is the significance of the limit obtained from the ratio test in relation to the convergence of a power series?

    -The limit obtained from the ratio test is significant because if it is less than one, it indicates that the power series converges absolutely within the interval determined by the values of x that satisfy this condition.

  • How does the video demonstrate the simplification of the ratio test formula for a power series?

    -The video demonstrates simplification by taking the ratio of the (n+1)th term to the nth term, simplifying the expression by canceling out like terms, and then taking the absolute value to find the limit as n approaches infinity.

  • What is the interior of the interval of convergence and how is it determined?

    -The interior of the interval of convergence is the range of x values for which the power series converges absolutely. It is determined by solving the inequality derived from the condition that the limit from the ratio test must be less than one.

  • How does the video illustrate the concept of the radius of convergence?

    -The video illustrates the radius of convergence by measuring the distance from the center of the interval (which is the point where the series is defined) to the endpoints of the interval of convergence.

  • What additional analysis is required to determine the exact interval of convergence beyond the interior?

    -To determine the exact interval of convergence, including the endpoints, additional analysis is required. This involves checking the behavior of the power series at the endpoints of the interval, often using tests other than the ratio test, to see if the series converges conditionally or diverges at those points.

  • What is the significance of the alternating harmonic series mentioned in the video?

    -The alternating harmonic series is significant because it is used as an example to show that the power series converges at a particular endpoint (x = 3 in the video). This series is known to converge, which helps in including that endpoint in the interval of convergence.

  • How does the video address the divergence of the harmonic series?

    -The video addresses the divergence of the harmonic series by plugging in a specific value of x (x = -3) into the power series and simplifying it to the harmonic series, which is known to diverge. This helps in determining that the endpoint x = -3 is not included in the interval of convergence.

  • What are some key takeaways or steps for finding the interval and radius of convergence as outlined in the video?

    -The key steps outlined in the video for finding the interval and radius of convergence include: 1) Running the ratio test to identify the interior of the interval of convergence, 2) Checking the endpoints using a non-ratio test to determine the exact interval, and 3) Measuring the radius of convergence from the center to the endpoints of the interval.

Outlines
00:00
📚 Understanding Interval and Radius of Convergence

This paragraph introduces the concept of interval and radius of convergence for power series. It explains that these concepts are an extension of the ratio test, which can be used to determine the values of X that make a power series converge absolutely. The speaker demonstrates how to apply the ratio test to a specific power series involving X, simplifying the terms and taking the limit as n approaches infinity. The result is an inequality that defines the interior of the interval of convergence. The speaker also discusses the need for further analysis to determine the exact interval of convergence, including checking the endpoints of the interval.

05:03
🔍 Analyzing the Interval of Convergence

In this paragraph, the speaker delves deeper into the analysis of the interval of convergence for a power series. They explain how to determine the radius of convergence by measuring the distance from the center of the interval to its endpoints. The speaker then checks the endpoints of the interval (-3 and 3) using a test other than the ratio test. They find that the series converges at x = 3 but diverges at x = -3, thus establishing the interval of convergence as -3 < x ≤ 3. The speaker also emphasizes the importance of understanding these concepts for solving problems in calculus and future studies in Taylor series.

10:04
📉 Exploring Different Power Series Scenarios

The final paragraph presents different scenarios involving power series and their convergence properties. The speaker discusses a series that converges conditionally at x = 2 and asks what happens at other values of x. They explain that the series is centered at x = 1 and that the radius of convergence is one, leading to an interval of convergence from 1 to 2. The speaker also considers what happens at x = 1.5, x = -1, and x = 0, concluding that x = 1.5 is within the interval of convergence, x = -1 is beyond the radius of convergence, and more information is needed to determine the behavior at x = 0. The paragraph concludes with a prompt for viewers to think about the implications of these scenarios and to seek further clarification if needed.

Mindmap
Keywords
💡Interval of Convergence
The 'Interval of Convergence' refers to the range of values for the variable x for which a power series converges. In the video, this concept is central to understanding the behavior of power series. The script uses the ratio test to determine the interval where the series converges absolutely, which is between -3 and 3, inclusive of the endpoint where the series converges conditionally.
💡Ratio Test
The 'Ratio Test' is a method used to determine the convergence of a series. The script explains that if the limit of the ratio of consecutive terms of a series approaches a value less than 1, the series converges absolutely. This test is applied to a power series with x as a variable to find the interval of convergence.
💡Power Series
A 'Power Series' is an infinite series of the form \( \sum_{n=0}^{\infty} a_n (x-c)^n \), where \( a_n \) are the coefficients and \( c \) is the center of the series. The video discusses the convergence properties of a specific power series and how to find its interval and radius of convergence.
💡Absolute Convergence
'Absolute Convergence' means that the series converges regardless of the order of its terms. The script mentions that if the limit from the ratio test is less than one, the power series converges absolutely within the interval of convergence.
💡Radius of Convergence
The 'Radius of Convergence' is the distance from the center of the power series to the nearest point where the series may not converge. The script calculates this by measuring the distance from the center (x=0) to the endpoints of the interval of convergence, which is 3 units in the discussed example.
💡Conditional Convergence
'Conditional Convergence' occurs when a series converges but not absolutely. The video script notes that conditional convergence is found at the endpoints of the interval of convergence and is used to determine whether the series converges at x=3.
💡Center of the Series
The 'Center of the Series' is the value of x about which the power series is centered. In the script, it is established that for the given power series, the center is at x=0, which is a crucial point for determining the radius of convergence.
💡Diverges
'Diverges' indicates that a series does not converge, meaning the sum does not approach a finite value. The script uses this term to describe what happens outside the interval of convergence, such as beyond x=3 where the series does not converge.
💡Alternating Harmonic Series
The 'Alternating Harmonic Series' is a specific type of series that the script mentions as an example of a series that converges. It is used to illustrate the behavior of the power series at the endpoint x=3, where the series converges conditionally.
💡Harmonic Series
The 'Harmonic Series' is a series of the form \( \sum_{n=1}^{\infty} \frac{1}{n} \). The script refers to this series to illustrate divergence, noting that when simplified to this form, the power series at x=-3 diverges, and thus x=-3 is not included in the interval of convergence.
💡Convergence Analysis
Convergence analysis involves determining whether a series converges and, if so, under what conditions. The script describes a step-by-step process for analyzing the convergence of a power series, including using the ratio test and checking endpoints, which is essential for understanding the series' behavior across different x values.
Highlights

Introduction to interval and radius of convergence for power series.

Extension of the ratio test discussion to determine convergence values.

The ratio test states that a series converges absolutely if the limit of the ratio of terms is less than one.

Demonstration of applying the ratio test to a series with variable X.

Explanation of setting up the ratio test with absolute values and the limit.

Simplification of the ratio test expression by grouping terms and canceling powers.

Taking the absolute value and determining the limit as n approaches infinity.

Analysis of the limit leading to the absolute value of x - 3 being less than one.

Solving the inequality to find the interior of the interval of convergence.

Diagram illustrating the interval of convergence between -3 and 3.

Explanation of divergence outside the interval -3 to 3.

Introduction to the concept of radius of convergence.

Determination of the radius of convergence as three units from the center.

Analysis of the end points -3 and 3 using a test other than the ratio test.

Inclusion of 3 in the interval of convergence as the power series converges at x = 3.

Exclusion of -3 from the interval of convergence due to divergence at x = -3.

Final interval of convergence specified as -3 < x ≤ 3.

Steps for finding the interval and radius of convergence summarized.

Importance of understanding interval of convergence in solving calculus problems highlighted.

Introduction to a different example involving conditional convergence at x = 2.

Determination of the radius of convergence for the second example as one unit.

Analysis of the power series at x = 1.5, x = -1, and x = 0 in the second example.

Explanation of the unknown nature of the series at x = 0 and the need for more information.

Transcripts

Browse More Related Video

AP Calculus BC Lesson 10.13 Part 2

Radius and Interval of Convergence

Calculus BC – 10.13 Radius and Interval of Convergence of Power Series

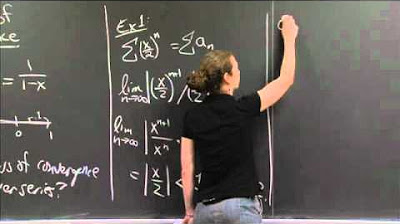
Ratio Test -- Radius of Convergence | MIT 18.01SC Single Variable Calculus, Fall 2010

Avon High School - AP Calculus BC - Topic 10.13 - Example 2

Avon High School - AP Calculus BC - Topic 10.13 - Example 3

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Power SeriesRatio TestConvergenceMathematicsTutorialInterval of ConvergenceRadius of ConvergenceAbsolute ConvergenceConditional ConvergenceTaylor Series