Definition of the Derivative Quickies

Chad Gilliland

24 Sept 201307:22

EducationalLearning

32 Likes 10 Comments

TLDRThis video script focuses on simplifying the process of finding derivatives using limit statements and derivative rules, avoiding extensive algebra. It reviews how to identify the function in question and apply power and chain rules directly, with examples including derivatives of 2x cubed and cosine of 5x. The script also touches on finding derivatives at specific points, like the derivative of sine at pi/6, using trigonometric knowledge.

Takeaways

📚 The video focuses on implicit differentiation and derivatives, aiming to review the process of finding derivatives from limit statements.
🔍 It emphasizes the importance of recognizing the function in the limit statement to avoid unnecessary algebra and directly apply derivative rules.
🔑 The first example illustrates how identifying the function \( f(x) = 2x^3 \) allows for the application of the power rule to find \( f'(x) = 6x^2 \) without extensive algebraic manipulation.
📈 The video introduces a shortcut for finding derivatives by recognizing the function and applying the appropriate derivative rules, such as the power rule and chain rule.
🌐 The second example demonstrates the use of the chain rule in conjunction with the derivative of cosine to find the derivative of \( \cos(5x) \), resulting in \( -5\sin(5x) \).
📝 The instructor encourages students to practice recognizing the function in the limit statement and applying derivative rules to find the derivative without full expansion.
📌 The video mentions the upcoming topic of related rates, indicating that mastery of implicit differentiation will be essential for understanding related rates.
📍 A specific point differentiation example is discussed, where the derivative at a particular point, such as \( \frac{\pi}{6} \), is sought.
📐 The example of finding the derivative of \( \sin(x) \) at \( \frac{\pi}{6} \) is used to illustrate the process of identifying the function and applying the derivative of sine, yielding \( \cos(\frac{\pi}{6}) = \frac{\sqrt{3}}{2} \).
🧩 The video script provides a method to simplify the process of finding derivatives from limit statements by leveraging the knowledge of derivative rules.
🔄 The instructor plans to revisit the topic the following day, reinforcing the importance of practice in recognizing functions and applying derivative rules efficiently.

Q & A

What is the main topic of the video script?
-The main topic of the video script is the review of taking derivatives, specifically focusing on implicit differentiation and the process of going from a limit statement directly to the derivative without extensive algebraic manipulation.
What is the purpose of reviewing limit statements in the context of derivatives?
-The purpose is to recognize the shortcuts that can be used to find derivatives, which will be useful when dealing with related rates in future lessons.
How does the script suggest simplifying the process of finding derivatives from a limit statement?
-The script suggests recognizing the function that is being differentiated and applying the appropriate derivative rules, such as the power rule or the chain rule, to find the derivative without the need for extensive algebraic expansion and simplification.
What is the power rule mentioned in the script and how is it applied?
-The power rule states that the derivative of x^n, where n is a constant, is n*x^(n-1). In the script, it is applied to find the derivative of 2x^3, which results in 6x^2.
What is the chain rule and how is it used in the script?
-The chain rule is a method for finding the derivative of a composite function. It states that the derivative of f(g(x)) is f'(g(x)) * g'(x). In the script, it is used to find the derivative of cos(5x), resulting in -5sin(5x).
What is the significance of recognizing the function f(x) in the process of taking derivatives from a limit statement?
-Recognizing the function f(x) allows for the direct application of derivative rules, simplifying the process and avoiding the need for algebraic manipulation of the limit statement.
What is the difference between finding the derivative in general and finding the derivative at a specific point?
-Finding the derivative in general gives a function that represents the slope of the original function at any point. Finding the derivative at a specific point gives the slope of the tangent line to the function at that particular point.
How does the script illustrate the process of finding the derivative of sine at a specific point?
-The script uses the limit statement involving sine of x at π/6, identifies the derivative of sine as cosine, and then evaluates the derivative at the specific point π/6, resulting in the cosine of π/6, which is √3/2.
What is the 30-60-90 triangle and how is it related to the script?
-A 30-60-90 triangle is a special right triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. The sides are in the ratio of 1:√3:2. The script uses this triangle to find the value of the cosine of 30 degrees, which is √3/2.
What is the importance of knowing certain values and derivatives without having to derive them each time?
-Knowing certain values and derivatives by heart is important because it allows for quicker problem-solving and a deeper understanding of the underlying principles in calculus, as demonstrated in the script with the sine and cosine functions.

Outlines

00:00

🧑‍🏫 Introduction to Implicit Differentiation

The speaker greets the audience and outlines the video’s focus on implicit differentiation and derivatives. They review the transition from limit statements to derivatives without extensive algebra. This foundational understanding will be crucial for mastering related rates. The example demonstrates recognizing the derivative form in a limit statement and applying derivative rules like the power rule to simplify the process.

05:06

📐 Example with Cosine Function

The speaker provides another example involving the limit of a difference quotient and identifies the function f(x) as cosine of 5x. They explain finding the derivative using the chain rule, resulting in -5 sin(5x). The emphasis is on recognizing f(x) and applying derivative rules without expanding terms.

🔍 Finding Derivatives at Specific Points

The speaker addresses more complex scenarios where the derivative is needed at a specific point, illustrated by an example with sine of x. They identify f(x) and the value a (π/6), confirming that sin(π/6) equals 1/2. The process involves recognizing f(x), taking its derivative, and evaluating it at the given point using trigonometric identities.

📏 Using Trigonometric Identities

A detailed explanation of finding the cosine of π/6 by drawing a 30-60-90 triangle and recalling key trigonometric identities. The speaker emphasizes the importance of knowing these identities for solving derivatives at specific points.

🔑 Conclusion and Practice Reminder

The speaker concludes by reminding viewers that they will practice these concepts, especially recognizing and applying derivative rules to limit statements, to avoid lengthy algebraic computations. They stress the importance of understanding these shortcuts and derivative rules for future lessons on related rates.

Mindmap

Keywords

💡Implicit Differentiation

Implicit differentiation is a method used in calculus to find the derivative of a function that is not explicitly given in terms of a single variable. In the video, the instructor is focusing on this technique and how it can be used to simplify the process of finding derivatives. The script mentions 'implicit differentiation' as a topic of review, indicating its importance in the lesson.

💡Derivatives

Derivatives in calculus represent the rate at which a function changes with respect to its variable. The video script discusses the process of finding derivatives, emphasizing a shortcut to identify the function and apply derivative rules directly, rather than going through extensive algebraic manipulation.

💡Limit Statement

A limit statement in calculus describes the value that a function or sequence approaches as the input approaches a certain value. The script uses the limit statement as a starting point for finding derivatives, particularly when the function is not explicitly given.

💡Difference Quotient

The difference quotient is a mathematical expression used to define the derivative of a function at a certain point. In the script, the instructor refers to the difference quotient as part of the process to identify the function whose derivative is being sought.

💡Power Rule

The power rule is a basic derivative rule that states the derivative of x to the power of n is n times x to the power of n-1. The script mentions the power rule as one of the derivative rules that students have learned and should apply to find the derivative of functions like 2x cubed.

💡Chain Rule

The chain rule is a fundamental theorem in calculus that allows the differentiation of composite functions. The script refers to the chain rule when discussing the derivative of cosine of 5x, where the derivative of cosine is multiplied by the derivative of the inside function, 5x.

💡Related Rates

Related rates problems in calculus involve finding the rate of change of one quantity given the rate of change of another related quantity. The script mentions that the class is leading into related rates, indicating that the skills of implicit differentiation are necessary for this topic.

💡Algebraic Manipulation

Algebraic manipulation refers to the process of rearranging and combining terms in an equation to simplify it or solve for a variable. The script suggests that there is a shortcut to avoid algebraic manipulation when finding derivatives by recognizing the function and applying derivative rules directly.

💡Specific Point

A specific point in calculus is a particular value of the variable at which a function or its derivative is evaluated. The script discusses finding the derivative at a specific point, such as the derivative of sine at pi/6, which requires identifying the function and then substituting the point into the derivative.

💡30-60-90 Triangle

A 30-60-90 triangle is a special right triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. The script uses the properties of a 30-60-90 triangle to find the value of the cosine of 30 degrees, which is needed to evaluate the derivative of sine at pi/6.

Highlights

Introduction to implicit differentiation and derivatives review.

Discussion on transitioning from limit statements to derivatives without extensive algebra.

Emphasis on recognizing the function to differentiate as a shortcut to finding the derivative.

Illustration of the process using the example of 2x cubed.

Application of the power rule to simplify finding the derivative.

Explanation of the difference quotient and its relation to the derivative.

Demonstration of using the chain rule in conjunction with the derivative of cosine.

Clarification on the derivative of cosine of 5x using the chain rule.

Introduction of the concept of finding the derivative at a specific point.

Analysis of a limit statement involving the derivative at a specific point, π/6.

Identification of the function sine of X and its derivative at π/6.

Use of trigonometric knowledge to find the derivative value at π/6.

Geometric approach using a 30-60-90 triangle to understand the derivative of sine at π/6.

Importance of recognizing and applying derivative rules to simplify limit statements.

Anticipation of further practice with related rates in upcoming lessons.

Encouragement for students to master the concepts for future lessons.

Transcripts

Browse More Related Video

AP Calculus AB: Lesson 3.1 Elementary Derivative Rules

1.5 - The Power and Sum Difference Rules

Derivatives of Trig Functions - Calculus | MCV4U

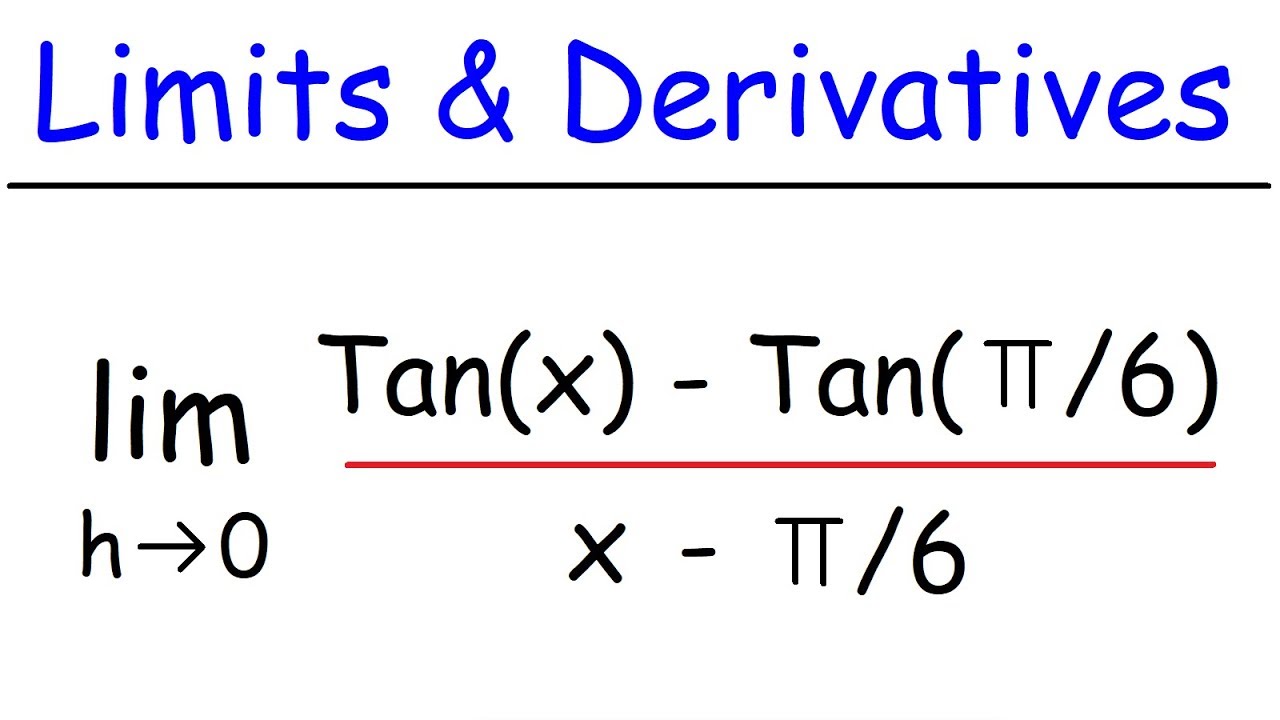
Limits and Derivatives

Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial

Exercises on Derivative Rules — Topic 56 of Machine Learning Foundations