13. Continuous Wavelets
TLDRThe video script introduces the concept of continuous wavelet transformations, a modern extension of Fourier analysis used for time-varying signal analysis. It highlights wavelets' practical applications, such as in digital image storage, and explains the limitations of traditional Fourier analysis in handling non-stationary signals. The script also discusses the uncertainty principle, fundamental to wavelet analysis and compression, and encourages viewers to explore wave packet exercises to understand this principle better.
Takeaways
- 🌟 The video introduces the concept of continuous wavelet transformations, a topic not commonly covered in traditional courses and often reserved for advanced studies.
- 📚 The subject matter is a modern extension of Fourier transforms, which is essential for understanding the analysis methods used by scientists in the field.
- 🔍 The script emphasizes the limitations of traditional Fourier analysis when dealing with non-stationary signals whose form changes over time, unlike stationary signals.
- 📷 The presenter's new digital camera serves as a practical example of wavelet applications, highlighting how wavelets are the basis for image storage in digital cameras.
- 📊 The script discusses the inadequacy of Fourier analysis for time-varying signals, as it lacks time resolution and is not suitable for data compression in applications like digital imaging.
- 🌐 The need for a model-independent, data-driven analysis is highlighted, which wavelets provide, making them an excellent tool for modern computing.
- 🌈 The video script presents three different types of wavelets, each with unique characteristics but sharing the common trait of oscillation and finite time existence.
- 📚 The 'uncertainty principle' is introduced as a fundamental theory behind wavelet analysis, relating the time and frequency widths of a wavelet and its Fourier transform.
- 📝 The script encourages viewers to perform exercises to understand wave packets and the uncertainty principle, emphasizing the computational aspect of wavelet analysis.
- 🔧 The exercises involve analyzing the width in time and frequency for different wave packets, applying the uncertainty principle to understand its practical implications.
- 🔄 The video concludes with a teaser for the next session, where Fourier analysis will be discussed in more detail, indicating a progressive learning approach.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is continuous wavelet transformations and their application.
How do wavelets differ from Fourier transforms?
-Wavelets provide better time resolution for signals that change over time, while Fourier transforms are better suited for stationary signals whose form does not change over time.
Why are wavelets particularly useful in modern computing?
-Wavelets are useful in modern computing because they allow for data compression and efficient analysis of signals that vary over time, such as images and seismic data.
What are some practical applications of wavelets mentioned in the lecture?
-Practical applications of wavelets mentioned include image storage in digital cameras, seismic analysis of earthquakes, brainwave analysis, and various fields of physics and geology.
What is the main limitation of Fourier analysis for non-stationary signals?
-The main limitation is that Fourier analysis does not provide time resolution, as it assumes that all frequencies are present at all times, making it unsuitable for signals that change over time.
What are the three types of wavelets shown in the lecture?
-The three types of wavelets shown are a Mexican hat (Gaussian with wings), a square wave, and a wiggly pulse.
What is a key advantage of wavelet analysis over Fourier analysis?
-A key advantage of wavelet analysis is its ability to provide time resolution, allowing for the localization of different frequencies at different times.
What is the uncertainty principle as it relates to wavelets?
-The uncertainty principle states that the product of the width in time and the width in frequency of a signal is always greater than 2π. This principle is fundamental to wavelet analysis and digital signal compression.
How do wavelets help in data compression?
-Wavelets help in data compression by allowing the representation of signals with fewer components, reducing the amount of data needed to store and transmit the signal without losing significant information.
What exercise does the lecturer suggest to understand wave packets and the uncertainty principle?
-The lecturer suggests estimating the width in time for three wave packets, calculating their Fourier transforms, determining the width in frequency, and verifying the uncertainty principle by multiplying the width in time by the width in frequency.
Outlines
🌌 Introduction to Continuous Wavelet Transformations
This paragraph introduces the topic of continuous wavelet transformations, a modern extension of Fourier transforms that are less commonly covered in traditional curricula. The speaker emphasizes the practical applications of wavelets, particularly in digital image storage, and hints at the analytical framework that will be discussed in more detail later. The introduction also includes a personal anecdote about the speaker's new digital camera, which serves as a real-world example of wavelet technology in action. The paragraph sets the stage for a deeper dive into the principles of wavelets, promising a gradual build-up to more complex topics.
🔍 Limitations of Discrete Fourier Transform and the Need for Wavelets
The speaker discusses the limitations of the Discrete Fourier Transform (DFT) when dealing with non-stationary signals, which are signals whose form changes over time. The DFT is shown to be ineffective for time-resolved frequency analysis and data compression in such cases due to the high correlation between its components. The paragraph introduces the need for a more model-independent, data-driven analysis tool, which is where wavelets come in. The speaker provides a brief overview of the versatility and applications of wavelets in various fields, and encourages the audience to look at the foundational wavelets that will be used for signal expansion.
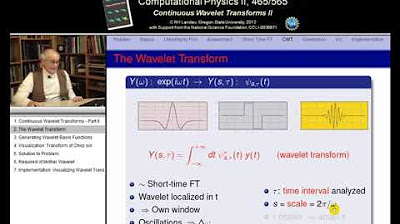
📊 The Concept of Wavelets and Wave Packets
This paragraph delves into the concept of wavelets and wave packets, explaining their importance in time-frequency analysis. The speaker describes wavelets as oscillating functions with finite time periods, which provide time resolution, and can be centered at different times. The paragraph introduces the 'mother wavelets' that generate 'daughter wavelets' of various sizes but the same shape, forming the basis for wavelet expansion. The speaker also touches upon the uncertainty principle, a fundamental theory behind wavelet compression and analysis, and illustrates it with an example of a wave packet and its Fourier transform.
📚 Exercises on Wave Packets and the Uncertainty Principle
The speaker concludes the script by assigning exercises to the audience to reinforce their understanding of wave packets and the uncertainty principle. The exercises involve analyzing three different types of wave packets: a pure Gaussian, a Gaussian multiplied by a sine function, and a Gaussian multiplied by a polynomial. The audience is asked to estimate the width in time (delta t) and frequency (delta omega) for each wave packet, using the full width at half maximum as a measure, and to verify the uncertainty principle by checking if the product of these widths is greater than two pi times a constant. The exercises aim to provide a practical application of the theoretical concepts discussed in the script.
Mindmap
Keywords
💡Continuous Wavelet Transform
💡Fourier Transform
💡Wavelet
💡Mother Wavelet
💡Time-Frequency Resolution
💡Uncertainty Principle
💡Wave Packet
💡Digital Camera
💡Data Compression
💡Principal Component Analysis
💡Computational Physics
Highlights
Introduction to the concept of continuous wavelet transformations, a modern extension of Fourier transforms.
Wavelet analysis is a less common topic in traditional curricula but is highly applicable in scientific fields.
Wavelet transformations are foundational in image storage for digital cameras, offering a practical application of the discussed theory.
The limitations of Fourier analysis in handling non-stationary signals and its implications for time resolution and data compression.
Wavelets provide a data or model-independent analysis, which is crucial for dynamic signal processing.
The basic idea of wavelets is to expand any arbitrary signal, especially those that vary over time, using wavelet bases.
Wavelets are characterized by their oscillation and finite period of existence in time, providing time resolution.
The concept of 'mother wavelets' that generate 'daughter wavelets' of various sizes but the same shape for wavelet expansion.
Wavelet analysis has found extensive applications in various fields such as physics, geology, and biology.
The uncertainty principle as the fundamental theory behind wavelet compression and analysis.
The relationship between the width in time and frequency space as derived from a single wave packet example.
The practical exercise of estimating the width in time and frequency for different types of wave packets to understand the uncertainty principle.
The importance of computational analysis in wavelet theory, as opposed to purely analytical methods.
The comparison between wavelet analysis and Fourier analysis in terms of their respective abilities to handle signal localization.
The role of wavelets in providing an extra degree of freedom over Fourier analysis, making it more suitable for computer-based analysis.
The practical value of wavelet analysis in digital image processing, as demonstrated by the speaker's new digital camera.
The speaker's personal anecdote about the acquisition of a new digital camera and its relation to the lecture topic.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: