13.4 Continuous Wavelet II
TLDRThis lecture delves into the fundamentals of continuous wavelet transformations, a powerful tool for analyzing non-stationary signals. It contrasts wavelets with the traditional Fourier analysis, highlighting the advantages of wavelets in capturing time-varying frequency components. The instructor guides through the concept of short-time Fourier transforms as a precursor to wavelets, explains how to generate wavelet bases, and discusses the implementation of wavelet transforms with visualizations. The session concludes with an assignment to apply wavelet transformations using different wavelets on various signals, providing hands-on experience with this versatile analysis method.
Takeaways
- 🌟 Continuous Wavelet Transforms (CWT) are discussed as an extension of Fourier Transforms, offering time-frequency analysis.
- 📚 The script introduces the concept of discrete wavelets, which are easier to compute but require understanding the transition from continuous wavelets.
- 🕒 The Short-Time Fourier Transform (STFT) is highlighted as a precursor to wavelets, analyzing signals in short time intervals with a window function.
- 🔍 Wavelets are used to analyze non-stationary signals where frequency components change over time, unlike traditional Fourier analysis which assumes constant frequencies.
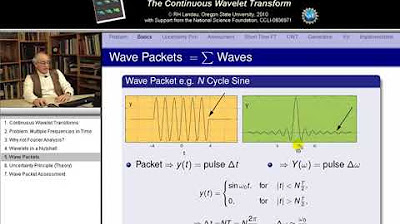
- 📉 The script explains the wavelet transform process involving a mother wavelet and how it is scaled and translated to analyze different frequencies and times.
- 🌐 The visualization of wavelets shows how they can capture both frequency and location in a signal, offering a time-scale representation.
- 🔢 The importance of scale in wavelet analysis is emphasized, with smaller scales corresponding to higher frequencies and larger scales to lower frequencies.
- 📝 The mathematical formulation of the wavelet transform is presented, including the integral over time with the wavelet function.
- 🖼️ The script discusses the practical application of wavelets in image processing, such as in digital cameras where raw data is transformed into a more compact wavelet representation.
- 🛠️ An assignment is given to implement wavelet transforms using different wavelets (Morlet, Mexican Hat, and Daubechies) and test them on various signals.
- 🔄 The script touches on the inversion of wavelet transforms to reconstruct signals from their wavelet coefficients, similar to how images are reconstructed from compressed data.
Q & A
What is the main focus of the lecture on wavelets?
-The lecture focuses on the basics of wavelets, specifically continuous wavelet transformations, and how they differ from Fourier transformations. It also introduces the concept of discrete wavelet transformations to be discussed in a subsequent lecture.
Why is the Fourier analysis not ideal for non-stationary signals?
-Fourier analysis is not ideal for non-stationary signals because it uses functions that exist for all times, leading to overlapping and correlated components. This makes it inefficient for analyzing signals with varying frequencies at different times since removing or altering one component affects the entire analysis.
What is the Short Time Fourier Transform and how does it improve upon the standard Fourier Transform?
-The Short Time Fourier Transform is a precursor to wavelets that overcomes some of the shortcomings of the standard Fourier Transform by performing a Fourier Transform over a short time interval. This is done by placing a 'window' over the data and analyzing a limited part of the signal at a time, which allows for better localization in time.
What is the role of the wavelet in a wavelet transform?
-In a wavelet transform, the wavelet is a function that is used to analyze the signal at different scales and positions. It is localized in time and has both a scale parameter and a time parameter, allowing for the analysis of the signal's frequency content at specific times and resolutions.
How does the wavelet transform handle the localization of the analysis in time?
-The wavelet transform uses wavelets that are localized in time, effectively serving as their own window function. This means that the analysis is localized without the need for a separate window function, as each wavelet covers a short time period and is translated and scaled to analyze different parts of the signal.
What is the significance of the scale parameter in a wavelet transform?
-The scale parameter in a wavelet transform is inversely proportional to frequency. It determines the level of detail or resolution at which the signal is analyzed. Small scale values correspond to high frequencies and fine details, while large scale values correspond to low frequencies and broader features.
How are wavelets generated for all possible scales and times?
-Wavelets for all possible scales and times are generated by taking a 'mother wavelet' and transforming it through scaling and translating operations. The mother wavelet is evaluated at different time shifts and scale factors to produce a family of 'daughter wavelets' that cover the entire time-frequency plane.
What is the mathematical expression for the Short Time Fourier Transform?
-The mathematical expression for the Short Time Fourier Transform involves an integral over time, with the signal multiplied by a window function and then transformed using the Fourier Transform formula, with the transform being a function of frequency (omega) and the center time (tor) of the window.
How does the wavelet transform differ from the Short Time Fourier Transform?
-While both the wavelet transform and the Short Time Fourier Transform use a window function to localize the analysis in time, the wavelet transform differs by using wavelets that are localized in both time and frequency, and by having a scale parameter that allows for the analysis of different frequencies at different times without the need for a separate window function.
What is the practical application of wavelet transforms in signal processing?
-Wavelet transforms are used in signal processing to analyze non-stationary signals, such as audio signals, images, and medical data. They allow for the extraction of detailed information about the signal's frequency content at different times, which is useful for tasks like denoising, compression, and feature extraction.
What is the assignment given at the end of the lecture?
-The assignment is to convert a program that previously performed a Discrete Fourier Transform (DFT) or a Continuous Fourier Transform (CFT) to perform a wavelet transform using three different wavelets: Morlet, Mexican Hat, and Daubechies. The students are then to test the wavelet transform on a sine wave, a sum of three different frequencies, and a non-stationary signal, and to attempt to invert the wavelet transform to reproduce the input signal.
Outlines
🌀 Introduction to Continuous Wavelet Transforms
This paragraph introduces the topic of wavelets, specifically focusing on the continuous wavelet transform (CWT). It sets the stage for a series of lectures that will explore both continuous and discrete wavelet transformations, drawing parallels with the Fourier transform and its discrete counterpart. The paragraph emphasizes the need for an analysis tool that can handle non-stationary signals with varying frequencies over time, pointing out the limitations of traditional Fourier analysis due to its global and time-invariant nature. The introduction of the short-time Fourier transform (STFT) as a precursor to wavelets is also mentioned, highlighting its ability to perform localized frequency analysis by using a sliding window function.
📊 Understanding Wavelet Transforms and Their Parameters
The second paragraph delves into the specifics of the wavelet transform, explaining the process and parameters involved. It contrasts the wavelet transform with the Fourier transform by describing the integration over a wavelet function rather than an exponential function. The paragraph introduces the scale and time parameters, 's' and 'tor', which are crucial for understanding the wavelet's frequency and time localization properties. It also discusses the concept of mother wavelets and daughter wavelets, illustrating how a single mother wavelet can be scaled and translated to generate a family of wavelets that can analyze different frequencies and time segments of a signal. The summary touches on the practical implications of wavelet transforms, such as their use in image processing and data compression.
🔍 Generating Wavelets at Various Scales and Frequencies
This paragraph explains the method of generating wavelets at all possible scales and frequencies to cover the entire time domain of a signal. It describes the use of a mother wavelet and how it can be transformed into daughter wavelets by scaling and translating. The process involves adjusting the scale to change the frequency content and translating the wavelet to different time positions. The explanation includes visual examples of how the wavelet changes with different scale and time parameters, emphasizing the flexibility and adaptability of wavelets in signal analysis. The paragraph also discusses the inverse wavelet transform and its application in reconstructing signals from their wavelet coefficients, drawing an analogy with digital cameras and image processing.
📈 Visualizing Wavelet Transforms and Inversion
The fourth paragraph provides a visualization of how wavelet transforms work in practice, using a chirp signal as an example. It describes the process of convoluting the signal with wavelets of varying scales and translating them to capture the signal's characteristics at different resolutions. The paragraph also explains the concept of wavelet coefficients and how they form a two-dimensional space that can be plotted as a surface plot. The discussion includes the inversion of the wavelet transform, which is akin to reconstructing the original signal from its wavelet coefficients, and it provides an example of how this can be done using a computer program.
📚 Mathematical Foundations and Properties of Wavelets
This paragraph discusses the mathematical foundations and properties necessary for wavelets to function effectively in signal analysis. It outlines the criteria that wavelets must meet, such as oscillation, localization, and the vanishing of the first p moments. The paragraph also emphasizes the importance of normalization in wavelet transforms and the need for consistency in mathematical treatment to ensure accurate analysis and inversion. It touches on the practical aspects of implementing wavelet transforms, including the assignment given to the audience to convert a program to perform wavelet transformations using different wavelets and test them on various signals.
🎓 Assignment and Future Discussion on Discrete Wavelets
The final paragraph concludes the lecture by assigning practical work to the audience, encouraging them to apply their understanding of wavelets by converting a program to perform wavelet transformations. The assignment involves using three different wavelets on specific test signals and checking the invertibility of the wavelet transform. The paragraph also previews the next lecture, which will focus on digitizing wavelets and making the process more discrete, thus building upon the foundation laid in this session.
Mindmap
Keywords
💡Wavelet Transform
💡Continuous Wavelet Transform (CWT)
💡Discrete Wavelet Transform (DWT)
💡Short-Time Fourier Transform (STFT)
💡Fourier Transform
💡Mother Wavelet
💡Scale
💡Time-Frequency Analysis
💡Signal
💡Inversion
💡Normalization
Highlights
Introduction to continuous wavelet transformations, a part two discussion focusing on how to perform a wavelet transform.
Comparison between continuous and discrete wavelet transformations, with an emphasis on the latter's simplicity and computational ease.
Wavelet transform basics, including the development of an analysis tool sensitive to the presence of different frequencies at different times.
Shortcomings of Fourier analysis and the evolution to short-term Fourier transform as a precursor to wavelets.
Explanation of the short-term Fourier transform, involving Fourier transforms in short time intervals with a window function.
Mathematical expression of the short-term Fourier transform, introducing the concept of window placement time.
Transition to wavelet transform, emphasizing the use of a wavelet function instead of an exponential function in Fourier analysis.
Description of the wavelet transform process involving a scale variable and a time variable, with an integral over time.
Visualization of the wavelet transform application, demonstrating how wavelets provide a localized analysis of signals.
Explanation of the mother wavelet and daughter wavelets, and how they are generated from a single mother wavelet by scaling and translating.
The concept of scale in wavelets, relating to the inverse of frequency and its importance in analyzing signal details.
Practical implementation of wavelet transforms using computer code, allowing users to explore and apply wavelet analysis.
The relationship between wavelet transforms and digital image processing, specifically in JPEG compression and RAW data handling.
Assignment details for converting a DFT or CFT program to perform wavelet transformations using three different wavelets.
Testing the wavelet transform on sine waves and non-stationary signals to validate the method's effectiveness.
The importance of wavelet properties such as oscillation, localization, and vanishing moments for successful signal analysis.
Homework assignment to apply wavelet transformations to various signals and attempt inversion to reproduce the original signal.
Upcoming discussion on digitizing wavelet transformations, making them more discrete for practical applications.
Transcripts
Browse More Related Video
13. Continuous Wavelets
But what is the Fourier Transform? A visual introduction.

12.5 The Discrete Fourier Transform (DFT) I

12.5 Discrete Fourier Transforms II

Quantum Physics: Part 2. Superposition. Particle in a box 🌚 Lecture for Sleep & Study

Baseball Stats: Rate and "Plus" Stats (OPS, wOBA, FIP, etc.)
5.0 / 5 (0 votes)
Thanks for rating: