12.5 The Discrete Fourier Transform (DFT) I
TLDRThis lecture delves into the practical application of computational Fourier analysis, contrasting theoretical discussions with hands-on approaches. The focus is on performing Fourier analysis on a computer, exploring the algorithm behind the Discrete Fourier Transform (DFT) and its implications for real-world data. The lecture covers signal synthesis, data compression, and transmission, emphasizing the mathematical foundations and practical constraints of dealing with finite datasets. The instructor guides through the steps of the DFT, from assumptions of periodicity to the calculation of frequency components, highlighting the importance of understanding both the theoretical and computational aspects of Fourier analysis.
Takeaways
- 📚 The lecture is focused on computational Fourier analysis, emphasizing the practical application over theoretical discussion.
- 🔍 The Fourier analysis is used to determine the number of frequencies and their magnitudes present in a signal.
- 🖥️ The process involves using a computer to perform Fourier analysis, which includes the use of the Discrete Fourier Transform (DFT).
- 📈 The DFT is essential for signal synthesis, data compression, and digital transmission, as it allows for the reconstruction of signals from their Fourier transforms.
- 🔄 The inverse transform is used to convert the Fourier spectrum back into the original signal, which is crucial for technologies like cellphones.
- ⚙️ The algorithm for DFT involves the use of the trapezoid rule for integration, which is an approximation method used due to the limitations of computer processing.
- 📉 The real-world constraints, such as measuring a finite number of signal points at discrete time intervals, affect the mathematical approach to Fourier analysis.
- 🔢 The DFT assumes periodicity of the signal, which helps resolve the ambiguity of the signal's behavior outside the measured time period.
- 🎛️ The frequency values in the DFT are discrete and determined by the total measurement time and the number of data points.
- 🔮 The lowest frequency that can be measured is inversely proportional to the total measurement time, indicating the resolution limit of the DFT.
- 📝 The final formula for the DFT is simple but requires an understanding of the underlying mathematical assumptions and approximations.
Q & A
What is the main focus of the lecture on computational Fourier analysis?
-The main focus of the lecture is to demonstrate how to perform Fourier analysis on a computer, covering the algorithm, the consequences of dealing with real experimental measurements, and the application of the Discrete Fourier Transform (DFT) for signal synthesis and data compression.
What are the two types of academics mentioned in the script, and what does the lecture represent?
-The script mentions two types of academics: those who enjoy discussing theoretical concepts and those who prefer practical application. The lecture represents the latter, focusing on the practical application of Fourier analysis.
What is the significance of the small simple formula mentioned in the script?
-The small simple formula is likely the DFT formula, which is crucial for understanding and applying Fourier analysis in computational settings. It is emphasized as something memorable and universally applicable once understood.
Why is the trapezoid rule used in approximating the integral in Fourier analysis?
-The trapezoid rule is used because it is a simple integration formula that matches the process of measuring a signal at discrete, equally spaced points, which is common in laboratory settings.
What is the role of the inverse transform in signal synthesis?
-The inverse transform is used to reconstruct a signal from its Fourier transform, which is essential for applications like cell phone technology where signals are transmitted as discrete values of different spectrum elements and then reconstructed into audible sound.
How does the discrete nature of real-world data measurements affect the mathematics of Fourier analysis?
-The discrete nature of real-world data measurements introduces constraints on the mathematics, requiring approximations and assumptions, such as periodicity, to deal with finite sets of data and the inverse problem of reconstructing signals from their spectra.
What is the Discrete Fourier Transform (DFT), and how does it solve the problem of finite data points?
-The DFT is a mathematical technique that provides a solution for analyzing a finite number of data points by making the minimum necessary assumptions. It allows for the transformation and analysis of signals within the constraints of real-world data limitations.
Why is the fundamental frequency of the data related to the number of data points and the time interval?
-The fundamental frequency is related to the number of data points and the time interval because it represents the smallest frequency that can be resolved within the given data set, which is determined by the total time of measurement divided by the number of points.
What is the consequence of assuming periodicity in Fourier analysis?
-Assuming periodicity in Fourier analysis leads to the consequence that the Fourier transform is only known at discrete values of frequency, and it implies that the function being analyzed repeats its pattern over the period considered.
How does the script explain the relationship between the time domain and the frequency domain in Fourier analysis?
-The script explains that the time domain maps into the frequency domain through the Fourier transform, with continuous time leading to a continuous frequency spectrum. However, due to real-world constraints, only discrete values of the frequency spectrum can be measured, which is addressed by the DFT.
Outlines
📚 Introduction to Computational Fourier Analysis
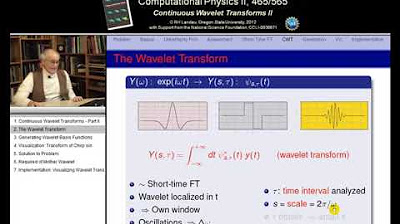
This paragraph introduces the lecture on computational Fourier analysis, contrasting theoretical discussion with practical application. The lecturer emphasizes the importance of not only understanding the theory but also applying it through computer-based analysis. The session's agenda includes discussing the algorithm, the impact of real-world data constraints on the mathematics involved, and the use of the discrete Fourier transform (DFT) for signal synthesis. The lecturer assures that by the end of the lecture, attendees will grasp a simple yet fundamental formula for Fourier analysis, which is essential for data compression and digital transmission.
🔍 Real-World Constraints in Fourier Analysis
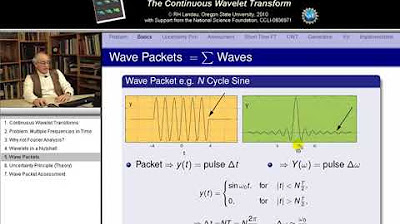
The second paragraph delves into the constraints imposed by the real world on Fourier analysis. It explains the limitations of measuring a finite number of signals at discrete time intervals, as opposed to the continuous time and frequency integrals required by the theory. The concept of the inverse problem in mathematics is introduced, which involves dealing with finite data sets to determine or reconstruct signals or their spectra. The discrete Fourier transform (DFT) is presented as a solution to this problem, making minimal assumptions to work with the given finite data points.
📈 Understanding Discrete Fourier Transform (DFT)
This paragraph provides a deeper understanding of the DFT, explaining how it deals with the reality of finite measurements and the periodicity assumption. It discusses the implications of these measurements on the transform's values, which are only known at discrete points corresponding to specific frequencies. The讲师clarifies the relationship between the total measurement time and the minimum discernible frequency, highlighting the fundamental frequency as a key aspect of the DFT. The summary also touches on the repetition of function values due to the periodicity assumption and how it affects the number of unique transform values.
🔢 The Mathematics of Discrete Fourier Transform
The fourth paragraph focuses on the mathematical formulation of the DFT, starting with the use of the trapezoid rule for approximating integrals. It describes how the Fourier transform is represented as a finite sum of complex exponentials, which simplifies to sines and cosines. The paragraph also explains the normalization process by dividing by the time step (1/h), leading to a simpler function for analysis. The inverse transform is also discussed, showing how it uses the same trigonometric functions to reconstruct the original signal from its Fourier spectrum.
🤔 Consequences of Applying DFT to Signals
The final paragraph in the input discusses the consequences of using the DFT on signals. It points out that the DFT assumes periodicity, which means that the analyzed signal or its Fourier spectrum will repeat if extended beyond the analyzed region. This repetition is a mathematical consequence of the assumptions made during the DFT process. The paragraph sets the stage for further discussion on the practical implications of these repeating patterns in signal analysis and synthesis.
Mindmap
Keywords
💡Computational Fourier Analysis
💡Fourier Transform
💡Discrete Fourier Transform (DFT)
💡Trapezoid Rule
💡Signal Synthesis
💡Data Analysis
💡Inverse Problem
💡Periodicity
💡Frequency Components
💡Algorithm
💡Numerical Integration
Highlights
Introduction to computational Fourier analysis and its practical application.
Differentiation between theoretical and practical academics in the context of Fourier analysis.
Explanation of the Fourier analysis process on a computer, emphasizing the importance of understanding the methodology.
Outline of the lecture covering algorithms, real-world data constraints, and signal synthesis.
Discussion on the limitations of experimental measurements and their impact on mathematical modeling.
Introduction to the Discrete Fourier Transform (DFT) and its role in signal synthesis.
The significance of the inverse transform in reconstructing signals from their Fourier transform.
Application of DFT in data compression and digital transmission.
The challenge of approximating infinite integrals in Fourier analysis using finite data points.
Use of the trapezoid rule for approximating integrals in Fourier series.
Consequences of approximations in Fourier analysis and their impact on the resulting series.
Real-world constraints in measuring signals and their effect on the Fourier transform.
The discrete nature of time steps and measurements in the context of the DFT.
Assumption of periodicity in signal measurement and its implications for Fourier analysis.
The relationship between the number of measurements and the discrete values of the Fourier transform.
Explanation of the frequency scaling in DFT and the determination of discrete frequency values.
The abstract concept of minimum frequency corresponding to maximum time in Fourier analysis.
Algorithmic steps for calculating the Fourier transform using the trapezoid rule.
The inverse Fourier transform and its application in signal reconstruction.
Consequences of the DFT's periodic nature on signal analysis and synthesis.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: