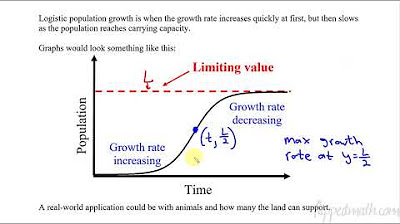
Logistic Differential Equation - Properties and Example

turksvids
25 Dec 201305:32
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial delves into the logistic differential equation, a crucial topic for Calculus BC students. The presenter explains the standard form of the equation and its solution, emphasizing the importance of memorizing the formula for quick problem-solving. Key insights include the equation's limit as X approaches infinity being 'L', regardless of initial conditions, and the behavior of the function concerning concavity and points of inflection. An example is provided to illustrate the process of solving the equation and finding the point of inflection, offering practical steps for students to follow.

Takeaways
  • 📚 The video discusses the logistic differential equation, a key topic for Calculus BC students.
  • 🔍 The logistic differential equation is presented in the form \( \frac{dy}{dx} = K \cdot y \cdot \left(1 - \frac{y}{L}\right) \).
  • 📝 An initial condition is necessary, typically given as \( y(0) = Y_0 \).
  • 🔑 The solution to the equation can be memorized and is derived using partial fractions and substitution, resulting in \( y = \frac{L}{1 + \frac{L - Y_0}{Y_0}e^{-Kx}} \).
  • 🌟 The limit of the solution as \( x \) approaches infinity is always \( L \), regardless of the initial condition.
  • 📈 If the initial condition is less than \( L \), \( Y \) is an increasing function and will have a point of inflection at \( y = \frac{L}{2} \).
  • 📉 If the initial condition is greater than \( L \), \( Y \) is a decreasing function and does not have a point of inflection.
  • 🔮 The concavity of the solution changes at \( y = \frac{L}{2} \), being concave up before and concave down after.
  • 📐 An example is provided to demonstrate how to manipulate the equation into the desired form and solve for the unknowns.
  • 🧭 The example also shows how to find the point of inflection by setting \( y \) to \( \frac{L}{2} \) and solving for \( x \).
  • 📝 The video concludes with a summary of the steps and concepts needed to work with the logistic differential equation, emphasizing memorization and application.
Q & A

  • What is the logistic differential equation?

    -The logistic differential equation is given by the formula dy/dx = K * y * (1 - y/L), where K is the growth rate, y is the dependent variable, and L is the carrying capacity.

  • What is the significance of the initial condition in the logistic differential equation?

    -The initial condition, typically y(0) = Y0, sets the starting point for the solution of the logistic differential equation and is crucial for determining the specific form of the solution.

  • What is the general form of the solution to the logistic differential equation?

    -The general solution to the logistic differential equation is y = L / (1 + (L - Y0) * e^(-Kx)), where Y0 is the initial condition and K, L are constants from the equation.

  • What does the parameter 'a' represent in the solution formula?

    -In the solution formula, 'a' is calculated as (L - Y0) / Y0 and is used in the exponential term to adjust the solution based on the initial condition.

  • What is the limit of the logistic differential equation solution as x approaches infinity?

    -The limit of the solution as x approaches infinity is L, regardless of the initial condition, which represents the carrying capacity of the environment.

  • How does the logistic differential equation behave if the initial condition is less than L?

    -If the initial condition is less than L, the solution y is an increasing function, and there will be a point of inflection when y equals L/2.

  • What happens if the initial condition is greater than L?

    -If the initial condition is greater than L, the solution y is a decreasing function, and there is no point of inflection because it does not reach y = L/2.

  • What is the process to find the solution of a logistic differential equation not in the standard form?

    -To find the solution, first, ensure the equation is in the standard form by factoring out constants. Then, identify K and L from the equation, calculate 'a', and use the memorized solution formula.

  • How can you find the point of inflection for the logistic differential equation?

    -To find the point of inflection, set the solution equal to L/2, solve for x, and this will give you the value of x where the inflection occurs.

  • Can you provide an example of solving a logistic differential equation with an initial condition?

    -Yes, for the equation dy/dx = 2 * y * (2 - y/4) with y(0) = 1, factor out the 2 to get it in standard form, identify K = 4 and L = 8, calculate 'a', and use the formula to find the solution y = 8 / (1 + 7 * e^(-4x)).

  • How do you determine the value of x for the point of inflection in the given example?

    -Set the solution y = 8 / (1 + 7 * e^(-4x)) equal to 4, solve for x, and you get x = 1/4 * ln(17/8), which is the x-value for the point of inflection.

Outlines
00:00
📊 Introduction to the Logistic Differential Equation

In this video, the logistic differential equation for Calculus BC is discussed. The equation is presented as dydx = K * y * (1 - y/L), with an initial condition y(0) = y0. The importance of the form of the equation is emphasized, and the solution is given as y = L / (1 + A * e^(-K * x)). A is defined as (L - y0) / y0. Key points include memorizing these forms and understanding that the limit of y as x approaches infinity is L, regardless of the initial condition. For initial conditions less than L, y is an increasing function with a point of inflection at y = L/2, while for initial conditions greater than L, y is a decreasing function without a point of inflection.

05:02
🔄 Example Problem and Solution Steps

An example problem is given: dydx = 2 * y * (2 - y/4) with the initial condition y(0) = 1. The equation is manipulated to fit the desired form by factoring out constants, resulting in K = 4 and L = 8. From the initial condition, a is calculated to be 7. The solution is then presented as y = 8 / (1 + 7 * e^(-4x)). The point of inflection is found by setting y equal to 4, solving for x, which results in x = (1/4) * ln(17). The explanation covers each step in detail, including solving for x and the properties of logarithms used.

Mindmap
Keywords
💡Logistic Differential Equation
The logistic differential equation is a type of equation used to model population growth. It takes the form dydx = K * y * (1 - y/L), where K is a constant, y is the population, and L is the carrying capacity. In the video, it is explained as a fundamental concept for Calculus BC students to understand, highlighting its application in predicting population limits and growth behaviors.
💡Initial Condition
An initial condition in differential equations specifies the value of the function at a particular point, usually where x = 0. In the video, the initial condition y(0) = y0 is used to solve the logistic differential equation. It is crucial for determining the specific solution to the differential equation given a starting point.
💡Carrying Capacity (L)
Carrying capacity, denoted as L, represents the maximum population size that an environment can sustain indefinitely. In the logistic differential equation, L is a key parameter that influences the behavior of the solution. The video emphasizes that the limit of the population as x approaches infinity will be L, regardless of the initial condition.
💡K (Growth Rate)
K is the growth rate constant in the logistic differential equation. It determines the speed at which the population grows or decays. In the video, K is identified and used to solve the differential equation, demonstrating how it affects the solution's behavior over time.
💡Point of Inflection
A point of inflection is where the curve changes concavity, from concave up to concave down or vice versa. In the logistic differential equation, this occurs when y = L/2. The video explains how to determine the point of inflection and its significance in understanding the population growth dynamics.
💡Partial Fractions
Partial fractions is a method used to break down complex rational expressions into simpler ones. In solving the logistic differential equation, partial fractions are employed to integrate and find the solution. The video mentions this technique as part of the process to derive the general solution.
💡Exponential Function
An exponential function is a mathematical function of the form e^(kx), where e is the base of natural logarithms and k is a constant. In the logistic differential equation solution y = L / (1 + A * e^(-kx)), the exponential function describes how the population approaches the carrying capacity over time. The video illustrates how this function fits into the solution.
💡Memorization
Memorization refers to the process of committing certain formulas or solutions to memory. The video suggests that students should memorize the general solution to the logistic differential equation and related formulas, as this will aid in solving problems more efficiently during exams.
💡Limit as x Approaches Infinity
The limit as x approaches infinity refers to the value that a function approaches as x becomes very large. In the context of the logistic differential equation, the video explains that the population will approach the carrying capacity L as time goes on, regardless of the initial condition.
💡Concavity
Concavity describes the curvature of a graph. A function is concave up if it curves upwards and concave down if it curves downwards. The video discusses how the logistic differential equation's solution changes concavity at y = L/2, providing insights into the population growth rate changes.
Highlights

Introduction to the logistic differential equation, a key topic for Calculus BC.

The logistic differential equation is presented in the form dy/dx = K * y * (1 - y/L).

The importance of having the differential equation in the correct form for solving.

The solution to the logistic differential equation involves partial fractions and clever substitution.

The general solution formula for the logistic differential equation is y = L / (1 + a * e^(Kx)) where a = (L - Y0) / Y0.

The limit of the solution as X approaches infinity is always L, regardless of the initial condition.

If the initial condition is less than L, Y is an increasing function with a point of inflection at y = L/2.

The concavity of the solution changes at y = L/2, going from concave up to concave down.

For initial conditions greater than L, the solution decreases monotonically without a point of inflection.

An example is provided with the differential equation dy/dx = 2 * y * (2 - y/4) and initial condition y(0) = 1.

The process of adjusting the equation to the desired form by factoring out constants.

Determining the limit of the solution as X approaches infinity from the adjusted equation.

Identifying the point of inflection for the solution when the initial condition is less than the limit.

Calculating the constant 'a' for the solution using the given initial condition and parameters.

The complete solution to the example equation is derived using the memorized formula and calculated constants.

Solving for the value of x at the point of inflection by setting the solution equal to L/2.

The final step involves using properties of natural logarithms to find the exact x-value for the point of inflection.

Conclusion summarizing the key points and processes involved in solving the logistic differential equation.

Transcripts

Browse More Related Video

Logistic Differential Equation

AP Calculus BC Lesson 7.9

2008 AP Calculus AB Free Response #5

Logistic Growth

Point of Inflection - Point of Inflexion - f''(x)=0 - Definition - How to Find - Worked Example 1

Calculus BC – 7.9 Logistic Models with Differential Equations

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Logistic EquationCalculus BCDifferential EquationsMathematics TutorialInitial ConditionsLimit AnalysisConcavityInflexion PointEducational ContentMath SolutionsLogistic Growth