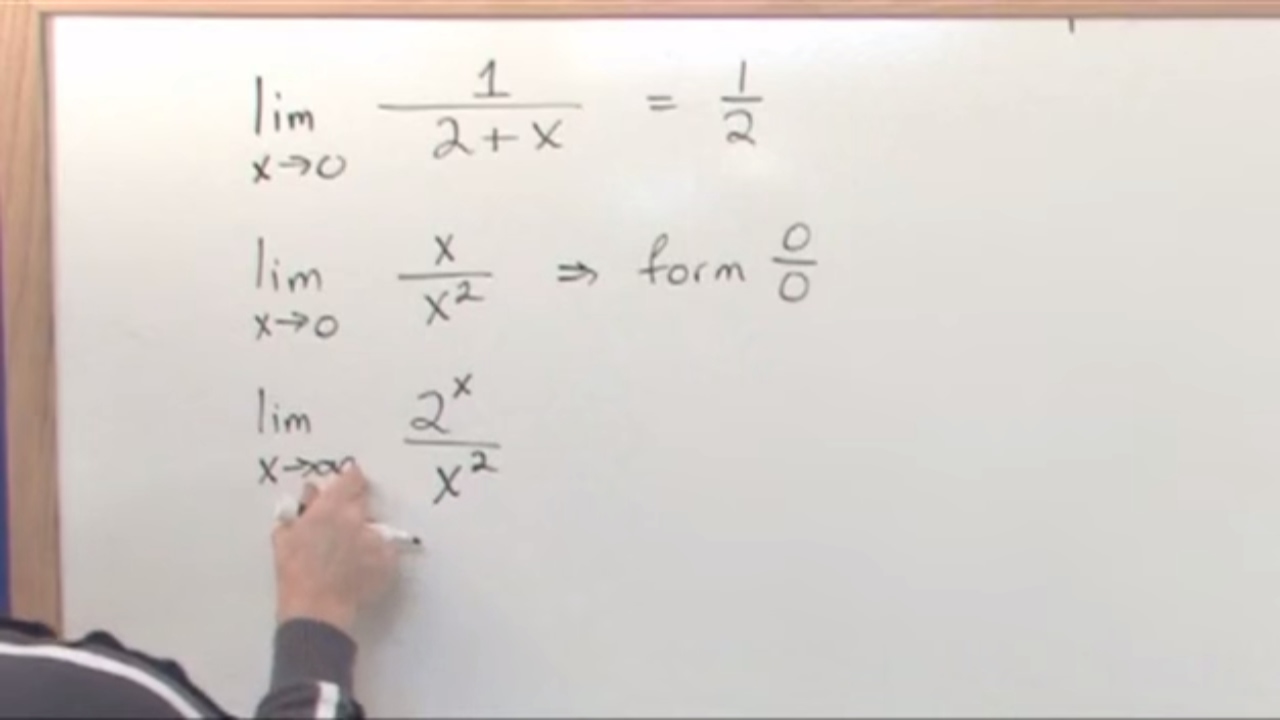Lec 35 | MIT 18.01 Single Variable Calculus, Fall 2007
TLDRThis MIT OpenCourseWare lecture introduces L'Hopital's Rule, a fundamental calculus technique for evaluating limits, particularly those involving indeterminate forms like 0/0 or ∞/∞. The professor explains the rule's application, demonstrates it with various examples, and highlights its utility in simplifying complex limit problems. The lecture also emphasizes the importance of verifying the rule's conditions before applying it and not relying on it excessively, reminding students to use basic algebraic skills alongside this powerful tool.
Takeaways
- 📚 The lecture introduces L'Hopital's Rule, a technique in calculus for finding limits that result in indeterminate forms such as 0/0 or ∞/∞.
- 🔍 L'Hopital's Rule is applicable when the limit of the ratio of two functions results in an indeterminate form, and it allows you to take the limit of the ratio of their derivatives instead.
- 👨🏫 The professor provides several examples to illustrate the application of L'Hopital's Rule, including limits involving exponential and logarithmic functions as x approaches infinity or 0.
- 📉 The rule can also be used to evaluate limits where the functions approach infinity, extending its use beyond just indeterminate forms at a specific point.
- 🤔 The professor emphasizes the importance of checking that the conditions for using L'Hopital's Rule are met, such as ensuring that the derivatives exist and the limit on the right-hand side exists or is infinite.
- 🧐 The lecture also compares L'Hopital's Rule with other methods of approximation, like linear approximation, showing that it can be a more powerful tool in certain situations.
- 📝 The professor demonstrates that L'Hopital's Rule can be applied multiple times if the limit remains indeterminate after the first application, but cautions against misuse by ensuring it's still applicable.
- 📉 The rule is particularly useful for limits involving exponential growth, where it can show that exponential functions grow faster than polynomial functions as x approaches infinity.
- 📚 The transcript includes a discussion on the behavior of logarithmic functions at infinity, showing that they grow much slower compared to any positive power of x.
- 🔍 The professor uses specific examples to highlight common mistakes, such as incorrectly applying L'Hopital's Rule when the limit is not in an indeterminate form.
- 📝 A reminder is given to not rely solely on L'Hopital's Rule and to use basic algebraic simplifications when dealing with limits, as they can often provide the answer more directly.
Q & A
What is the main topic discussed in the script?
-The main topic discussed in the script is L'Hopital's Rule, a method in calculus for evaluating limits, especially those involving indeterminate forms such as 0/0 or infinity/infinity.
What does the professor clarify about the pronunciation and spelling of L'Hopital's Rule?
-The professor clarifies that L'Hopital's Rule is also known as L'Hospital's Rule. The circumflex in 'Hopital' is a French notation to omit the 's', and it is still pronounced 'L'Hopital' even with an 's' in it.
Can L'Hopital's Rule be used to find limits as x approaches infinity?
-Yes, L'Hopital's Rule can be used to find limits as x approaches infinity. The rule is applicable to both 0/0 and infinity/infinity indeterminate forms, including when x approaches infinity.
What is an indeterminate form in calculus?
-An indeterminate form in calculus is an expression that does not provide enough information to determine the limit, such as 0/0, infinity/infinity, 0 times infinity, and infinity minus infinity.
How does the professor illustrate the concept of L'Hopital's Rule using an example?
-The professor illustrates the concept of L'Hopital's Rule using the example of the limit as x approaches 1 of (x^10 - 1) / (x^2 - 1). By dividing both the numerator and the denominator by (x - 1), the limit can be evaluated using the derivatives of the numerator and denominator.
What is the condition for applying L'Hopital's Rule?
-L'Hopital's Rule can be applied when the limit of the ratio of two functions results in an indeterminate form of 0/0 or infinity/infinity, and the limit of the ratio of their derivatives exists.
Why is it important to check if the limit still results in an indeterminate form after applying L'Hopital's Rule?
-It is important to check if the limit still results in an indeterminate form after applying L'Hopital's Rule because the rule can only be applied if the condition of an indeterminate form is met. If the form is no longer indeterminate, the rule cannot be used.
What is the relationship between L'Hopital's Rule and linear approximations?
-The relationship between L'Hopital's Rule and linear approximations is that L'Hopital's Rule essentially uses the linear approximations of the functions involved at the point of interest, which is the basis for the rule's application.
Can L'Hopital's Rule be applied multiple times if the limit remains indeterminate after the first application?
-Yes, L'Hopital's Rule can be applied multiple times if the limit remains indeterminate after the first application, as long as the conditions for an indeterminate form are still met after each differentiation.
What is the professor's advice on using L'Hopital's Rule in relation to basic algebra?
-The professor advises not to use L'Hopital's Rule as a crutch and to remember basic algebra skills when evaluating limits. He emphasizes that one should identify and simplify the main terms of an expression before resorting to L'Hopital's Rule.
Outlines
📚 Introduction to L'Hopital's Rule
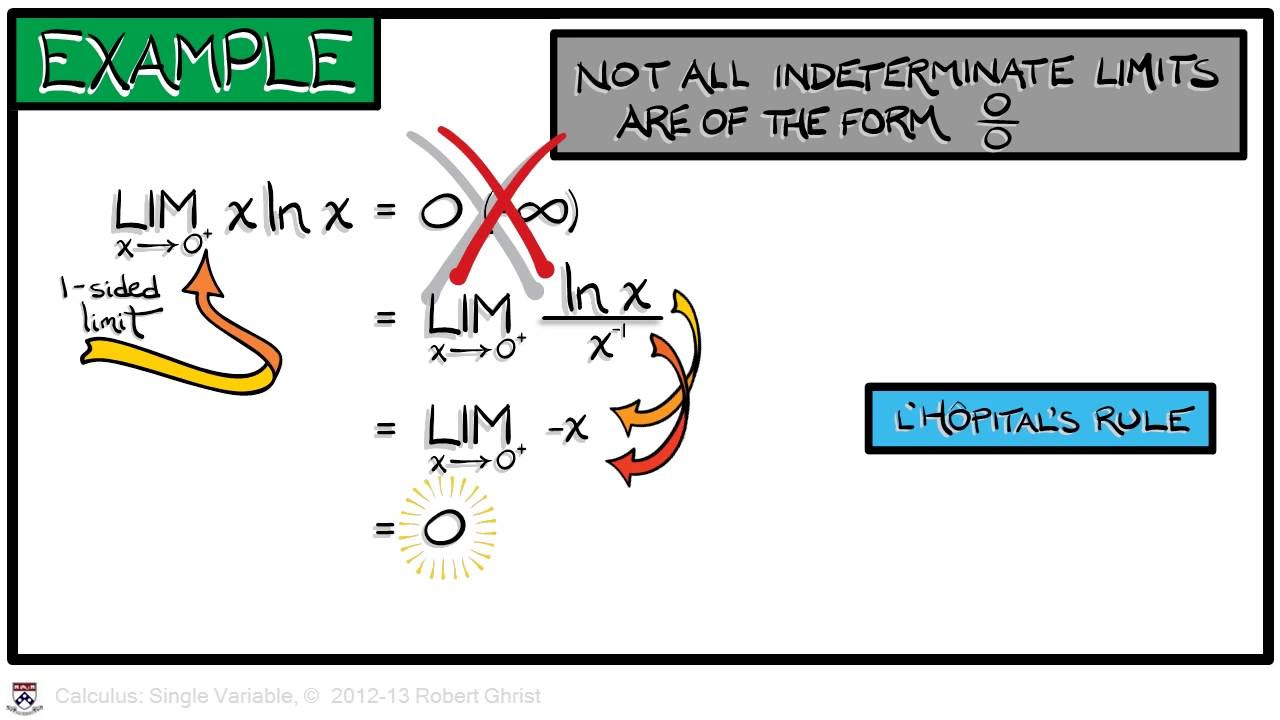
This paragraph introduces L'Hopital's Rule, a fundamental calculus technique for evaluating limits, particularly those involving indeterminate forms like 0/0 or infinity/infinity. The professor explains that the rule is named after L'Hopital, with the correct pronunciation despite the presence of an 's' in the name. The rule provides a systematic way to calculate limits that may not be easily determined through basic substitution, such as x ln x as x approaches infinity or x approaches 0 from the positive side. The professor illustrates the concept with an example of a limit that results in an indeterminate form and hints at the method's systematic approach and generalization.
🔍 Exploring L'Hopital's Rule with an Example
The professor delves into the specifics of L'Hopital's Rule by examining a concrete example: the limit as x approaches 1 of (x^10 - 1) / (x^2 - 1). This example showcases an indeterminate form of 0/0 when x equals 1. To address this, the professor suggests a trick from earlier in the course: dividing both the numerator and the denominator by (x - 1) to simplify the expression. The idea is then connected to the concept of a difference quotient, which is a precursor to the derivative. The paragraph concludes with the setup for a more systematic approach to L'Hopital's Rule.
📘 Formulating L'Hopital's Rule - Version 1
In this section, the professor formulates the first version of L'Hopital's Rule. The rule is presented as a method to evaluate limits of the form f(x) / g(x) as x approaches a certain value 'a', where both f(a) and g(a) are zero, resulting in an indeterminate form of 0/0. The rule states that under these conditions, the limit of the original function can be found by taking the limit of the ratio of their derivatives, f'(x) / g'(x), as x approaches 'a'. The professor emphasizes that this method is valid provided that g'(a) is not zero. The paragraph also addresses a student's question about the intuitive understanding of the procedure, suggesting that it relates to linear approximations of the functions involved.
📙 Enhancing L'Hopital's Rule - Version 2
Building upon the first version, the professor introduces an enhanced version of L'Hopital's Rule that can handle cases where the denominator is not zero. The rule is restated to assert that the limit of f(x) / g(x) as x approaches 'a' is equal to the limit of f'(x) / g'(x), provided that f(a) = g(a) = 0, creating an indeterminate form, and the right-hand side limit exists. The professor provides examples to illustrate the application of this rule, including the limit of sin(5x) / sin(2x) as x approaches 0, which simplifies to 5/2 using the rule. The paragraph emphasizes the ease of applying L'Hopital's Rule and its utility in simplifying complex limits.
🔑 Applying L'Hopital's Rule to Indeterminate Forms
The professor continues to explore L'Hopital's Rule, demonstrating its application to various indeterminate forms. The rule is applied to the function cos(x) - 1 / x^2 as x approaches 0, which initially results in another indeterminate form. However, the professor shows that applying the rule again leads to a determinate result. The justification for this repeated application is that if the final limit exists, it validates all preceding limits. The professor also discusses the importance of ensuring that the rule's conditions are met, particularly the existence of the right-hand limit.
🌐 Expanding L'Hopital's Rule to Infinite Limits
This paragraph expands the applicability of L'Hopital's Rule to include limits as x approaches infinity, as well as cases where f(a) and g(a) are infinite. The professor clarifies that the rule can handle not only 0/0 indeterminate forms but also infinity/infinity scenarios. Additionally, it is mentioned that the right-hand side of the limit can be finite, infinite, or negative infinite, as long as it is not wildly oscillating. The paragraph emphasizes the rule's versatility and its usefulness in a wide range of limit calculations.
📊 Demonstrating L'Hopital's Rule with Exponential and Logarithmic Functions
The professor provides examples to demonstrate the application of L'Hopital's Rule to exponential and logarithmic functions. The examples include the limits of x ln(x) as x approaches 0 and x e^(-x) as x approaches infinity. The professor shows that by converting products into ratios and applying the rule, these limits can be simplified and evaluated. The examples highlight the rule's effectiveness in determining the behavior of functions at extreme values, such as infinity.
📈 Comparing L'Hopital's Rule with Approximation Methods
The professor compares L'Hopital's Rule with approximation methods, such as linear and quadratic approximations, for evaluating limits. Examples given include the limits of sin(5x)/sin(2x) as x approaches 0 and cos(x) - 1 / x^2 as x approaches 0. The comparison shows that both methods can yield the same result, but L'Hopital's Rule may be more straightforward in certain cases. The paragraph emphasizes the importance of understanding the underlying concepts and the conditions under which each method is applicable.
🚫 The Pitfalls of Misapplying L'Hopital's Rule
The professor warns against the misuse of L'Hopital's Rule, illustrating how it can lead to incorrect conclusions if not applied properly. An example is given where the second application of the rule results in an incorrect limit due to the loss of the indeterminate form. The professor emphasizes the importance of checking that the conditions for L'Hopital's Rule are still met after each application. The paragraph serves as a cautionary note to ensure that students use the rule carefully and with proper understanding.
📘 Concluding Remarks on L'Hopital's Rule
In the final paragraph, the professor concludes the discussion on L'Hopital's Rule by emphasizing the importance of not over-relying on it as a crutch. The professor advises students to use their algebraic skills to simplify expressions before resorting to the rule and to remember their basic mathematical senses. An example is provided to show how simplifying an expression algebraically can lead to the correct limit without the need for multiple applications of L'Hopital's Rule. The paragraph ends with a reminder to see the professor next time, indicating the end of the lesson.
Mindmap
Keywords
💡L'Hopital's Rule
💡Indeterminate Form
💡Derivative
💡Limit
💡Infinity
💡Linear Approximation
💡Quotient Rule
💡Differentiation
💡Exponential Function
💡Logarithm
Highlights
Introduction to L'Hopital's Rule as a method to calculate limits involving infinity.
L'Hopital's Rule can be applied to new types of limits, such as x ln x as x approaches infinity.
The rule is also applicable to limits as x approaches 0 from the positive side, such as x e^(-x).
L'Hopital's Rule provides a systematic way to understand limits rather than relying on calculators.
Illustration of the rule using an example from the first unit of the class, x^10 - 1 / x^2 - 1.
Explanation of indeterminate forms like 0/0 and how L'Hopital's Rule can be used to resolve them.
Technique of dividing by x - 1 to simplify limits and the connection to derivatives.
Generalization of the method to handle limits where f(a) = g(a) = 0.
Derivation of L'Hopital's Rule from the concept of difference quotients and derivatives.
Formulation of L'Hopital's Rule in Version 1, including conditions for its application.
Examples of applying L'Hopital's Rule to various limits, such as sin(5x) / sin(2x) as x approaches 0.
Demonstration of how L'Hopital's Rule simplifies the process of finding limits compared to other methods.
Clarification on the necessity of the right-hand limit existing for the application of L'Hopital's Rule.
Discussion on the intuitive understanding of L'Hopital's Rule through linearization.
Comparison of L'Hopital's Rule with approximation methods and their consistency.
Expansion of L'Hopital's Rule to handle limits involving infinity and not just indeterminate forms.
Examples illustrating the rule's application to exponential functions and their growth relative to polynomial functions.
Explanation of the behavior of logarithmic functions at infinity using L'Hopital's Rule.
Cautionary advice on the correct application of L'Hopital's Rule and the importance of checking for indeterminate forms.
Emphasis on not over-relying on L'Hopital's Rule and the importance of basic algebra in evaluating limits.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: