Physics - Basic Introduction

The Organic Chemistry Tutor

29 Dec 202053:37

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script introduces fundamental physics concepts, including displacement, velocity, acceleration, projectile motion, Newton's laws, and forces. It explains how distance differs from displacement, the relationship between speed and velocity, and the impact of gravitational acceleration on vertical motion. The script uses examples to illustrate these principles, such as a person walking in different directions and a ball being thrown or dropped, making complex ideas accessible for beginners.

Takeaways

📏 Distance is a scalar quantity that represents the total path length traveled, regardless of direction.
📍 Displacement is a vector quantity that accounts for both the magnitude and direction of an object's change in position.
🚶‍♂️ An example given in the script illustrates that John's total distance traveled is 11 meters, but his displacement is only 5 meters due to his change in direction.
🚗 Speed is the rate at which an object covers distance and is always a positive scalar quantity, whereas velocity can be negative, indicating direction.
⏱ The formula d = vt is used to calculate distance, where d is distance, v is speed, and t is time.
🔢 Average speed is calculated by dividing the total distance traveled by the total time, while average velocity is the total displacement divided by the total time.
🏎 Acceleration is the rate of change of velocity over time and can be positive or negative, indicating whether the object is speeding up or slowing down.
🚀 Gravitational acceleration, represented by 'g', is the acceleration due to Earth's gravity, which is approximately -9.8 m/s² downward.
🌐 Projectile motion involves an object moving under the influence of gravity, with constant horizontal velocity (vx) and changing vertical velocity (vy) affected by gravity.
📚 Newton's first law, the law of inertia, states that an object at rest will stay at rest, and an object in motion will stay in motion with a constant velocity unless acted upon by a net external force.
🔄 Newton's second law, F = ma, describes the relationship between force, mass, and acceleration, indicating that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.

Q & A

What is the difference between distance and displacement?
-Distance is a scalar quantity that refers to the total path length traveled by an object, regardless of direction. Displacement, on the other hand, is a vector quantity that considers both the magnitude and direction of the movement from the initial to the final position.
Can displacement be negative?
-Yes, displacement can be negative. It is negative when the direction of movement is opposite to the chosen reference direction, typically associated with the negative x or y-axis in a coordinate system.
What is the formula to calculate the time it takes for an object to travel a certain distance at a constant speed?
-The formula to calculate time (t) when the distance (d) and speed (v) are known is t = d / v.
How is the difference between speed and velocity exemplified in the script?
-Speed is a scalar quantity that only has magnitude and indicates how fast an object is moving. Velocity is a vector quantity that includes both magnitude and direction, indicating both how fast and in which direction an object is moving.
What is the formula for calculating average speed?
-Average speed is calculated by dividing the total distance traveled by the total time taken, represented by the formula v_avg = d_total / t_total.
How does the script differentiate between average speed and average velocity?
-Average speed is the total distance divided by the total time, whereas average velocity is the total displacement divided by the total time. Average speed does not account for direction, while average velocity does.
What does acceleration measure?
-Acceleration measures how quickly the velocity of an object changes over time. It is the rate at which an object speeds up or slows down.
What is the standard gravitational acceleration on Earth?
-The standard gravitational acceleration on Earth is approximately -9.8 meters per second squared, acting downward (negative y-direction).
How does the script explain the effect of gravitational acceleration on an object's vertical velocity?
-The script explains that gravitational acceleration affects the vertical component of an object's velocity (v_y), causing it to decrease if the object is moving upward or increase if the object is moving downward.
What is projectile motion and how does it relate to the concepts of velocity and acceleration discussed in the script?
-Projectile motion is the motion of an object that is influenced only by gravity, typically launched into the air and moving under the influence of gravity. In projectile motion, the horizontal velocity (v_x) remains constant if no other horizontal forces are acting on it, while the vertical velocity (v_y) is affected by gravitational acceleration.
Can you explain Newton's first law of motion as described in the script?
-Newton's first law of motion, also known as the law of inertia, states that an object at rest will remain at rest, and an object in motion will continue in motion with a constant velocity, unless acted upon by a net external force.
What is the equation representing Newton's second law of motion?
-Newton's second law of motion is represented by the equation F_net = m * a, where F_net is the net force acting on an object, m is the mass of the object, and a is the acceleration of the object.

Outlines

00:00

📏 Distance and Displacement Basics

This paragraph introduces fundamental concepts in physics such as distance, displacement, velocity, acceleration, and projectile motion. Distance is the scalar quantity representing the total path traveled by an object, while displacement is a vector quantity that includes both magnitude and direction, representing the change in position from start to finish. The example of John walking east and then west illustrates the difference between the total distance traveled and the net displacement. The paragraph emphasizes the importance of understanding the directional aspect of displacement and the distinction between scalar and vector quantities.

05:02

🚗 Understanding Speed and Velocity

The second paragraph delves into the concepts of speed and velocity. Speed is a scalar quantity that measures how fast an object is moving without regard to direction, while velocity is a vector quantity that includes both speed and direction. The paragraph clarifies the difference between the two by providing examples, such as a train moving at a constant speed without direction and a train moving west with a specified velocity. It also explains the formulas for calculating average speed and average velocity, highlighting the importance of recognizing the directional component in velocity calculations.

10:04

⏱️ Time and Motion Analysis

This paragraph continues the discussion on motion by examining the relationship between time, distance, speed, and velocity. It uses the formula d = vt to demonstrate how distance traveled can be calculated given speed and time, or vice versa. The paragraph poses a question to the viewer, asking them to calculate the time it would take for an object to travel a certain distance at a given speed, providing a step-by-step solution to reinforce the concept.

15:06

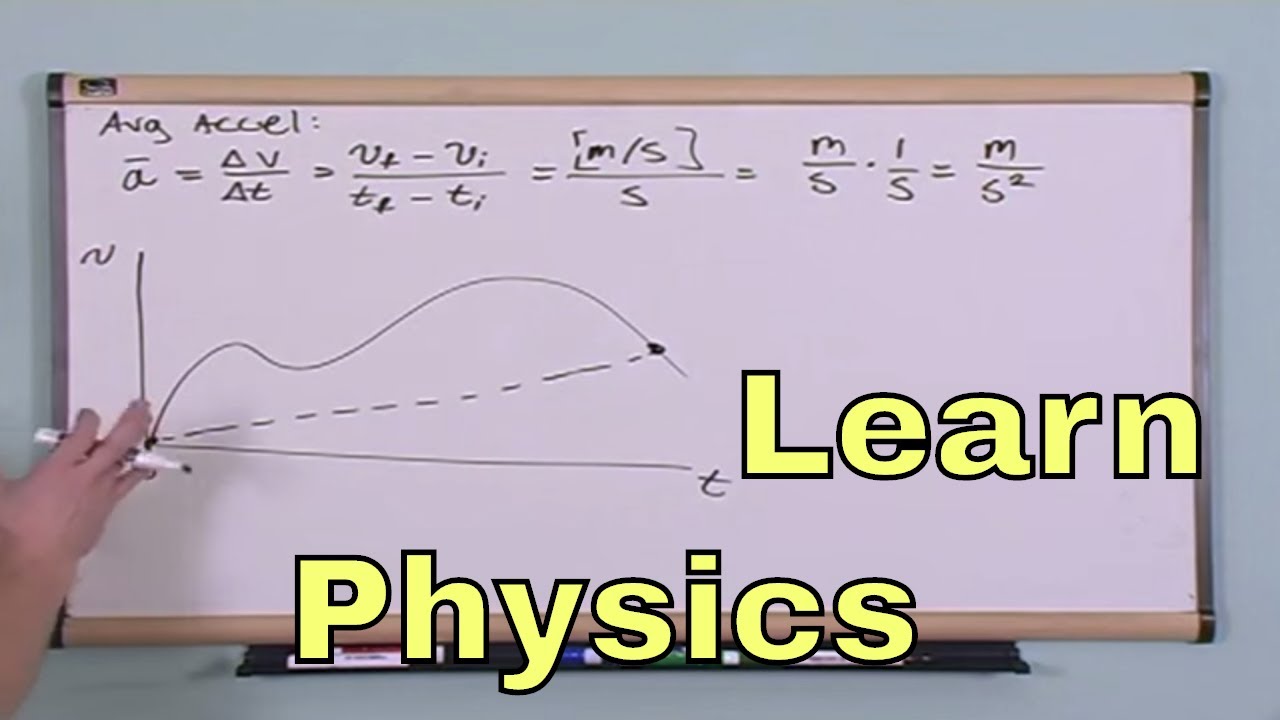
🚀 Acceleration and Changes in Velocity

Acceleration is the focus of this paragraph, which explains how it measures the rate of change of velocity over time. The paragraph contrasts acceleration with velocity, emphasizing that acceleration can be positive or negative, indicating a change in speed in either direction. It provides examples of a truck and a sports car to illustrate the concept of acceleration, showing how the sports car has a greater acceleration due to its quicker increase in speed. The paragraph also introduces the formula for calculating acceleration and uses it to compare the acceleration of the two vehicles.

20:06

📉 Deceleration and the Role of Gravity

The concept of deceleration is explored in this paragraph, using the example of an object moving with an initial velocity and then slowing down due to a negative acceleration. The paragraph explains that if the direction of acceleration is opposite to the direction of velocity, the object is slowing down. It also introduces gravitational acceleration, denoted by 'g', and explains its effect on vertical velocity, using the moon's gravitational acceleration as a comparative example.

25:07

🌍 Gravitational Acceleration and Its Effects

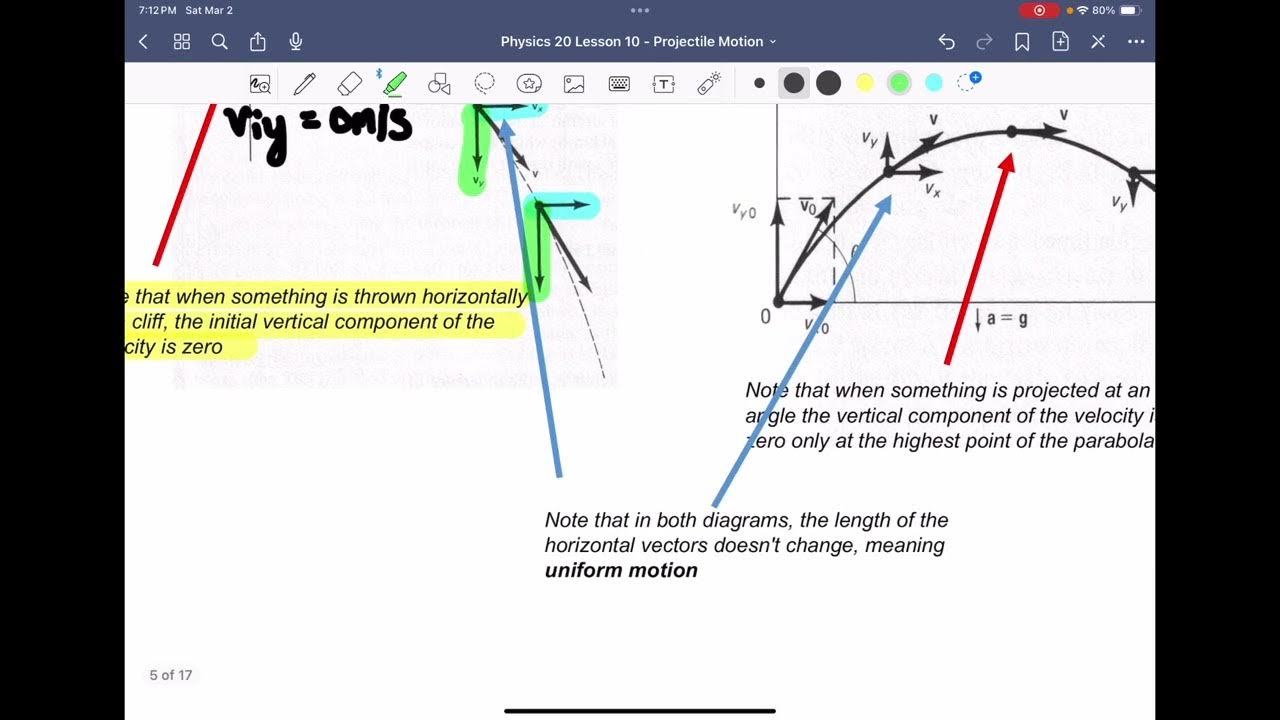
This paragraph further discusses gravitational acceleration, specifically its role in affecting the vertical component of an object's velocity. It clarifies that gravitational acceleration does not influence the horizontal velocity, using the example of a ball being released from rest at the top of a cliff. The paragraph illustrates how the vertical velocity of the ball changes over time due to the constant acceleration of gravity, resulting in an increase in speed towards the ground.

30:09

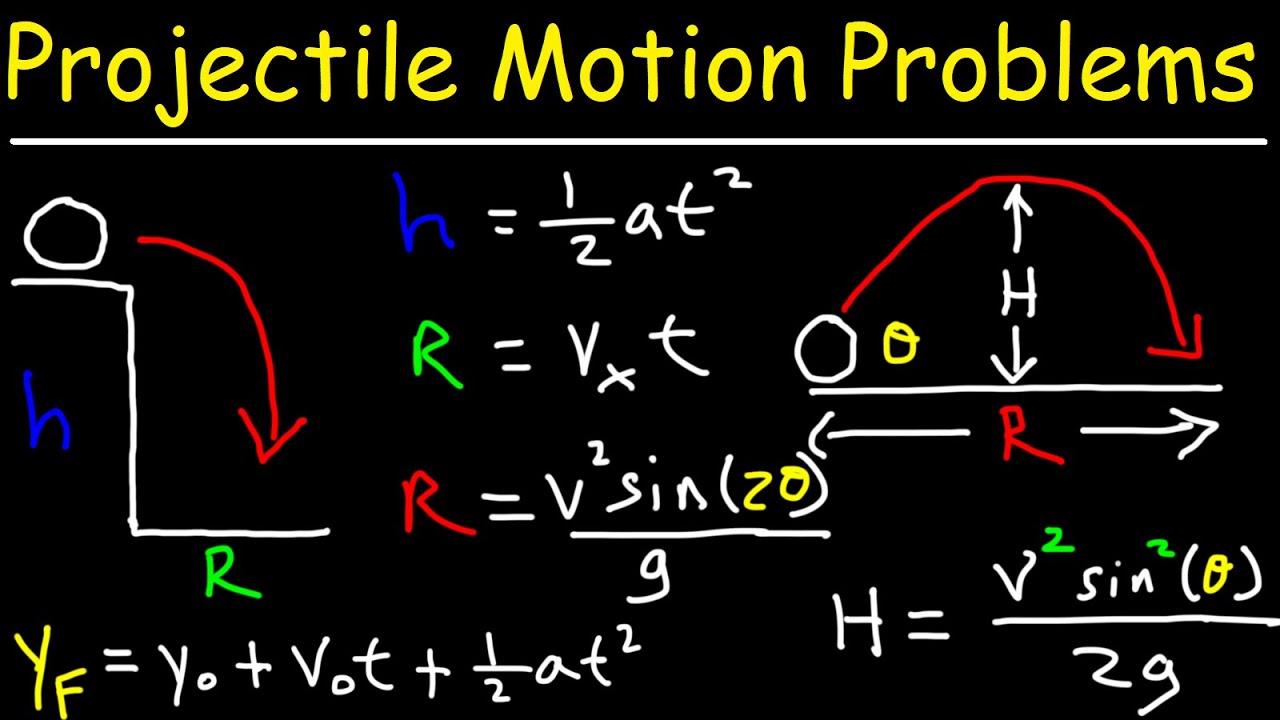
🏹 Projectile Motion and Its Components

The paragraph introduces projectile motion, explaining it as the movement of an object under the influence of gravity. It differentiates between one-dimensional and two-dimensional projectile motion, using examples of a ball falling straight down and a ball kicked off a cliff. The paragraph emphasizes that in typical projectile motion problems, horizontal velocity remains constant due to the absence of horizontal acceleration, while vertical velocity is affected by gravitational acceleration.

35:12

🔄 Newton's First Law of Motion

Newton's first law of motion is the focus of this paragraph, which states that an object at rest will remain at rest, and an object in motion will continue in motion unless acted upon by a net force. The paragraph explains this concept with examples of a box at rest and a box in motion, illustrating how forces such as pushing or pulling, including friction, can change the state of motion of the object. It also touches on the idea of motion in space, where objects can move for extended periods due to the near absence of friction.

40:13

🚀 Newton's Second Law of Motion

This paragraph presents Newton's second law of motion, which relates the net force acting on an object to its mass and acceleration. The paragraph provides an equation, F = ma, to demonstrate how the net force is calculated and how it results in acceleration. An example is given to calculate the acceleration of a 10-kilogram mass when a force of 80 newtons is applied, showing that the box will accelerate at a rate of 8 meters per second squared, leading to an increase in velocity over time.

Mindmap

Keywords

💡Displacement

Displacement is the vector quantity that refers to the change in position of an object. It includes both magnitude (how far) and direction. In the script, displacement is illustrated by the example of a person named John who walks 8 meters east and then 3 meters west, resulting in a net displacement of 5 meters to the east. This concept is crucial for understanding motion because it accounts for directionality, unlike distance, which is a scalar quantity and only measures the total path traveled regardless of direction.

💡Distance

Distance is a scalar quantity that represents the total path length traveled by an object, without considering direction. It is mentioned in the script when explaining the difference between distance and displacement. For example, John's total path traveled is 11 meters (8 east and 3 west), which is the distance. Distance is always a positive value and is essential for understanding the overall length of a journey, but it does not provide information about the direction of motion.

💡Velocity

Velocity is a vector quantity that describes the rate of change of an object's position, including both the speed (how fast) and direction of the object. The script distinguishes velocity from speed by stating that velocity can be positive or negative, indicating direction (e.g., eastward or westward). For instance, if a car is moving at 30 meters per second west, its velocity would be -30 m/s, indicating the direction and speed. Velocity is integral to the study of motion as it provides a comprehensive description of an object's movement over time.

💡Speed

Speed is a scalar quantity that indicates how fast an object is moving, without regard to its direction. It is always a positive value. In the script, speed is exemplified by the formula d = vt, where 'v' represents speed, and 't' represents time. Speed is a fundamental concept in physics for describing the rapidity of motion but does not convey directional information. For example, a car traveling at 60 miles per hour has a speed of 60 mph, regardless of the direction it is heading.

💡Acceleration

Acceleration is the rate of change of velocity per unit time. It is a vector quantity, indicating that it has both magnitude and direction. The script explains that acceleration occurs when a vehicle's speed increases or decreases over time, such as a sports car accelerating from 0 to 60 miles per hour faster than a truck. A key formula introduced in the script is acceleration = (final velocity - initial velocity) / time, which is used to calculate how quickly the velocity of an object is changing.

💡Gravitational Acceleration

Gravitational acceleration, often denoted as 'g', is the acceleration due to gravity that acts on objects near the Earth's surface. It is approximately -9.8 m/s² downward, which means it acts in the negative y-direction. The script uses gravitational acceleration to explain how the vertical component of an object's velocity (v_y) changes over time when the object is in free fall. For example, if a ball is dropped, its vertical velocity will decrease by 9.8 m/s each second due to the gravitational pull of the Earth.

💡Projectile Motion

Projectile motion is the motion of an object thrown or launched into the air, where it is influenced only by its initial velocity and the acceleration due to gravity. The script discusses both one-dimensional and two-dimensional projectile motion. In one dimension, the object moves either vertically upwards or downwards. In two dimensions, the object has both a horizontal and vertical component to its motion, forming a parabolic trajectory. The script explains that horizontal velocity (v_x) remains constant in the absence of other forces, while the vertical velocity (v_y) changes due to gravity.

💡Newton's First Law

Newton's first law, also known as the law of inertia, states that an object at rest will remain at rest, and an object in motion will continue in motion with a constant velocity, unless acted upon by a net external force. The script illustrates this with examples of a box sliding on a surface, where friction is the force that eventually stops the box. Without friction or any other force, the box would continue moving indefinitely, demonstrating the principle of inertia.

💡Newton's Second Law

Newton's second law of motion relates the net force acting on an object to its mass and acceleration. The script provides the formula F = ma, where 'F' is the net force, 'm' is the mass, and 'a' is the acceleration. This law is fundamental for understanding how the application of a force results in a change in the motion of an object. For example, if a 10 kg object is subjected to a force of 80 N, it will accelerate at 8 m/s², as explained in the script.

💡Force

In the context of the script, force is described as a push or pull action that can cause an object to change its state of motion. It is a vector quantity, having both magnitude and direction. The script mentions that forces can be applied in various ways, such as pushing a box or pulling it with a rope (tension force). Forces are essential in understanding changes in motion, as per Newton's laws, and are responsible for accelerating objects or changing their velocity.

Highlights

Basic concepts such as displacement, velocity, acceleration, projectile motion, Newton's three laws, forces, and momentum are covered in the video.

Distance is the total path length traveled, while displacement includes both magnitude and direction from the initial to the final position.

Displacement is a vector quantity, whereas distance is a scalar quantity.

Speed is the rate at which an object covers distance, measured in meters per second, and is always positive.

Velocity is a vector quantity that includes both speed and direction, and can be positive or negative.

The formula d = vt is used to calculate distance, where d is distance, v is speed, and t is time.

Average speed is calculated by dividing the total distance traveled by the total time, while average velocity is displacement divided by time.

Acceleration is the rate at which velocity changes, and it is defined as the change in velocity divided by the change in time.

Gravitational acceleration, denoted as g, is -9.8 m/s² on Earth and affects the vertical component of velocity.

In projectile motion, the horizontal velocity (vx) remains constant unless acted upon by a force, while the vertical velocity (vy) changes due to gravity.

Projectile motion can be analyzed in two dimensions, considering both horizontal and vertical components of velocity.

Newton's first law of motion states that an object at rest will remain at rest, and an object in motion will continue in motion unless acted upon by a net force.

Friction is a force that opposes motion and can bring an object in motion to rest.

Newton's second law of motion is summarized by the equation F = ma, where F is the net force, m is mass, and a is acceleration.

The net force applied to an object results in an acceleration that changes the object's velocity.

In the absence of friction, objects can move indefinitely, illustrating the concept of inertia.

Tension force is a type of force that acts through a rope, pulling objects in the direction of the rope.

Transcripts

Browse More Related Video

Physics for Beginners (Ep-1) | Motion | Basic Physics

How to Cram Kinematics in 1 hour for AP Physics 1

How To Solve Projectile Motion Problems In Physics

AP Physics 1 Workbook 1.N Projectile Motion Part 2 Solution

Physics 20 Unit A Lesson 10: Projectile Motion

01 - Velocity And Acceleration In 1-D (Physics Tutor)

Related Tags

Physics Basics Displacement Velocity Acceleration Projectile Motion Newton's Laws Forces Momentum Gravitational Acceleration Motion Analysis Educational Video