How to Cram Kinematics in 1 hour for AP Physics 1
TLDRIn this academic coaching session, Eugene dives into the fundamentals of kinematics, focusing on the critical concepts of displacement, velocity, and acceleration. He clarifies the difference between distance and displacement, and how velocity and acceleration are vector quantities. Eugene uses real-world examples, such as free fall and projectile motion, to illustrate these concepts and their applications. He also explains how to analyze velocity-time and position-time graphs, providing insights into calculating velocity and acceleration from graphical data. The session is enriched with practical examples and equations essential for understanding AP Physics 1, making complex topics accessible for students.
Takeaways
- 📚 Kinematics is a fundamental part of mechanics that focuses on how an object moves, not why.
- 📌 Displacement is a vector quantity that represents the change in position from initial to final, while distance is the total path length traveled.
- 🏃♂️ Velocity is a vector quantity that describes the rate of change of displacement, and is distinct from speed, which is a scalar quantity.
- 🚀 Acceleration is the rate of change of velocity, and it is also a vector quantity, indicating both magnitude and direction.
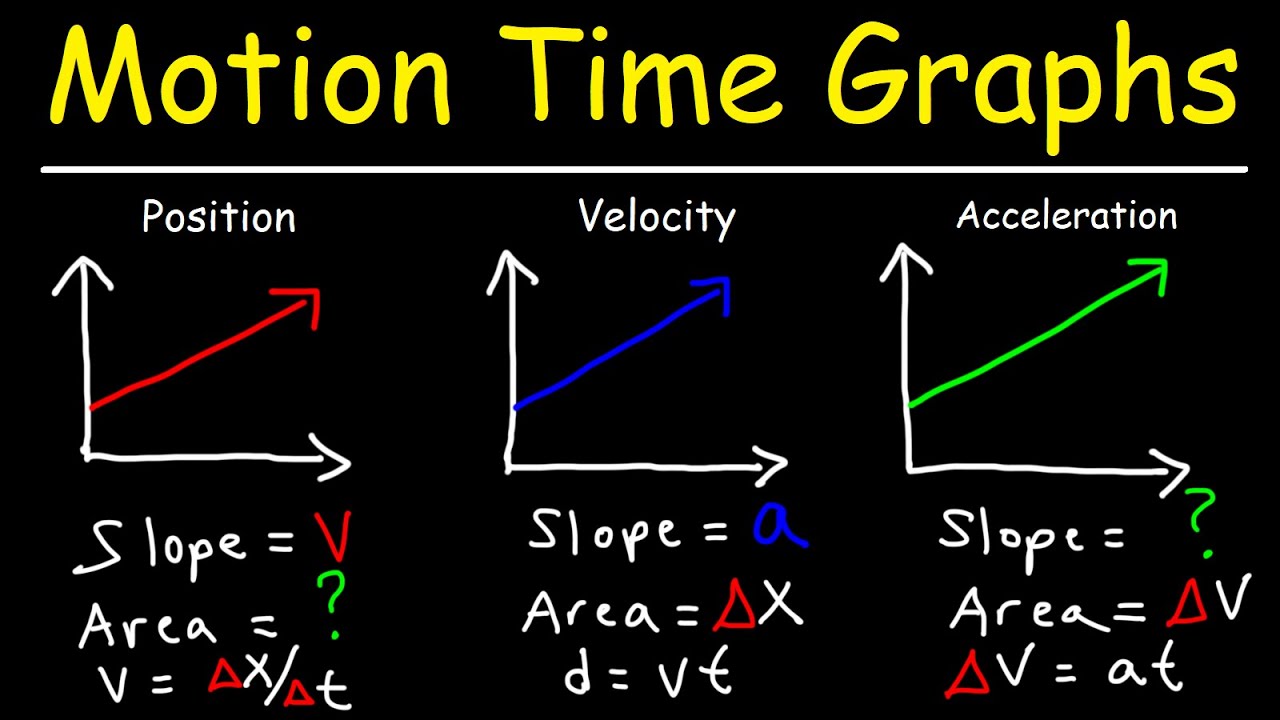
- 📈 In analyzing motion, graphs such as displacement vs. time and velocity vs. time can be used to determine an object's motion characteristics.
- 🌐 Projectile motion, such as throwing an object, involves both horizontal and vertical components of motion that can be analyzed separately.
- 🔢 The equations of motion (specifically, the three key equations mentioned in the script) are essential for calculating various aspects of motion in kinematics.
- 📊 Velocity vs. time graphs can be used to find both velocity and acceleration, as well as to calculate displacement through the area under the curve.
- 🎯 Understanding the difference between speeding up/slowing down (related to speed) and accelerating/decelerating (related to velocity) is crucial for analyzing motion.
- 🌟 Free fall is a type of motion where an object is subject only to gravitational acceleration, with no air resistance, and is a classic example of constant acceleration motion.
Q & A
What is the main focus of kinematics in the study of mechanics?
-The main focus of kinematics is to study how an object moves, without delving into the reasons behind its motion. It looks at aspects such as the direction of movement, whether the motion is linear or curved, and if there is acceleration or deceleration involved.
What is the difference between displacement and distance in kinematics?
-Displacement is a vector quantity that represents the change in position of an object, focusing on the initial and final positions. Distance, on the other hand, is a scalar quantity that measures the total path length traveled by the object.
How is velocity different from speed?
-Velocity is a vector quantity that considers both the speed (magnitude) of an object and its direction of motion. Speed is a scalar quantity that only measures how fast an object is moving, without regard to direction.
What does acceleration tell us about an object's motion?
-Acceleration tells us how quickly the velocity of an object is changing. It is a vector quantity, meaning it has both magnitude and direction, and it indicates whether an object is speeding up, slowing down, or changing direction.
How can you determine the acceleration of an object from a velocity-time graph?
-The acceleration of an object can be determined from a velocity-time graph by calculating the slope of the graph line. A constant slope indicates a constant acceleration, while a changing slope suggests a variable acceleration.
What is the significance of the area under a velocity-time graph?
-The area under a velocity-time graph represents the change in position or displacement of the object. It is calculated by finding the area bounded by the graph curve, the horizontal axis, and the vertical lines marking the time interval of interest.
How does the initial velocity and gravitational acceleration affect the motion of a ball thrown vertically upward?
-In the case of a ball thrown vertically upward, the initial velocity will cause the ball to move upwards against gravity (which acts as a constant downward acceleration). At the peak of its trajectory, the ball's vertical velocity will be zero before it starts to fall back down to Earth, following the same path but in reverse due to the constant gravitational acceleration.
What is the relationship between displacement, velocity, and acceleration in the context of projectile motion?
-In projectile motion, displacement, velocity, and acceleration are all vector quantities and are related through their components. The horizontal component of velocity (Vx) remains constant because there is no horizontal acceleration, while the vertical component of velocity (Vy) changes due to gravitational acceleration. The displacement follows a parabolic path because of the combination of constant horizontal velocity and accelerating (or decelerating) vertical velocity.
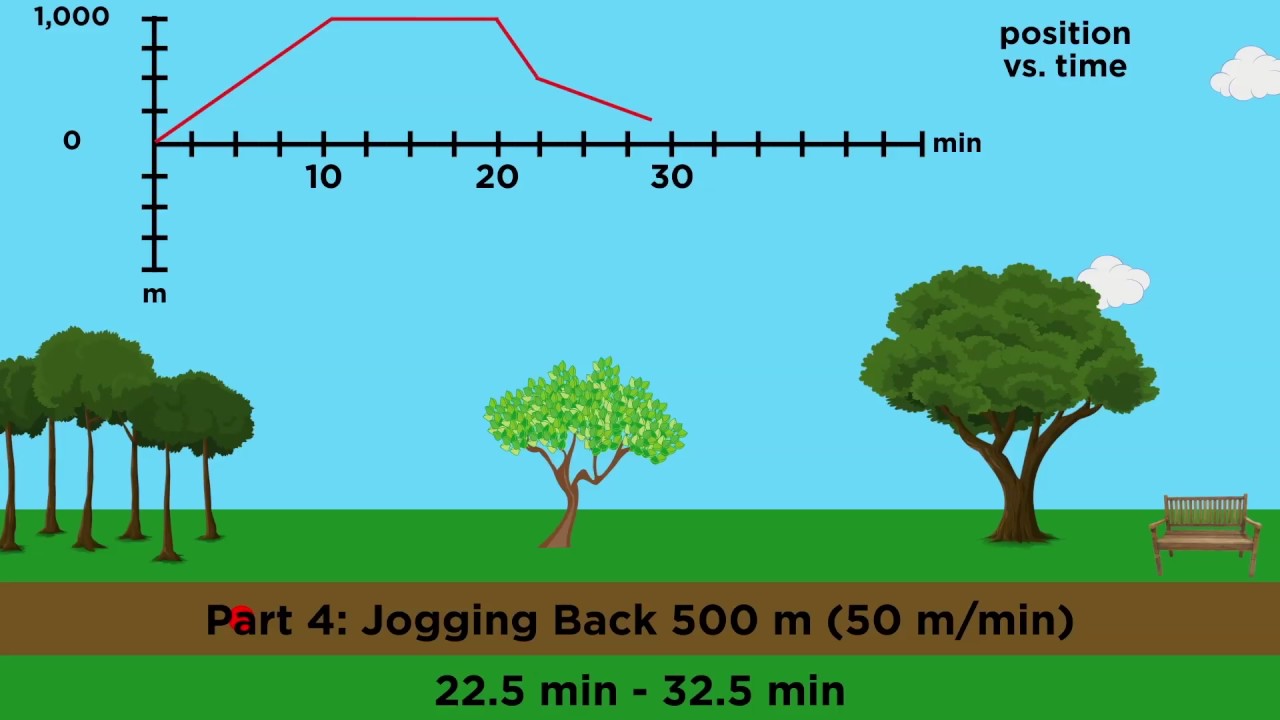
How can you calculate the average velocity of an object from a position-time graph?
-The average velocity of an object can be calculated from a position-time graph by determining the total displacement (change in position) over the total time interval. This is represented by the area under the graph divided by the time interval considered.
What is the significance of the slope in a position-time graph?
-The slope in a position-time graph represents the instantaneous rate of change of position with respect to time, which is equivalent to the instantaneous velocity of the object. A constant slope indicates a constant velocity, while a changing slope indicates a changing velocity, which is acceleration or deceleration.
Outlines
📚 Introduction to Kinematics and Vector Quantities
This paragraph introduces the topic of kinematics, emphasizing its importance in understanding mechanics. Eugene, the academic coach, explains that kinematics focuses on how an object moves, not why, and distinguishes between displacement and distance. Displacement, a vector quantity, is defined by the change in position from initial to final, while distance includes all paths traveled. The paragraph also highlights the difference between velocity and speed, with velocity being a vector quantity that considers both magnitude and direction. Acceleration is introduced as the rate of change in velocity, and the importance of vector quantities in physics is reiterated.
📈 Analyzing Velocity and Displacement Graphs
The second paragraph delves into the analysis of velocity versus time and displacement versus time graphs. It explains how the position of an object changes over time and how this is represented graphically. The concept of a curved line indicating changing position is discussed, along with the interpretation of the tangent line's slope as velocity. The paragraph also covers how to calculate velocity from a position-time graph and introduces the concept of acceleration through the change in velocity over time. The constant acceleration motion is exemplified, and the relationship between displacement, velocity, and acceleration is further clarified.
🚗 Real-World Examples of Linear Motion
This paragraph provides real-world examples of linear motion, such as free fall, and explains the concept of gravitational acceleration. It discusses how the velocity of a falling object increases due to gravity and how the direction of velocity and acceleration affect the object's speed. The paragraph also differentiates between speeding up and slowing down in terms of velocity and acceleration, using examples of objects moving in positive and negative directions. The importance of understanding the relationship between velocity, acceleration, and direction is emphasized.
🏐 Projectile Motion and Two-Dimensional Kinematics
The fourth paragraph introduces projectile motion as a type of two-dimensional kinematics, where an object is influenced only by gravity and air resistance is negligible. The initial velocity's components are discussed, and how they change over time due to gravitational acceleration. The paragraph explains that while the horizontal component of velocity remains constant, the vertical component changes, resulting in a parabolic path. The concept of acceleration being constant in both magnitude and direction is reiterated, and the relationship between velocity components and the path of projectile motion is clarified.
📝 Equations for Constant Acceleration Motion
This paragraph presents three key equations used in kinematics for constant acceleration motion: the final velocity equation, the final position equation, and the displacement equation. An additional equation relating the change in position to the average velocity is introduced. The conditions under which these equations are applicable are discussed, emphasizing that both the magnitude and direction of acceleration must remain constant. The paragraph also explains how the area under the velocity-time graph represents displacement and how this concept can be used to solve problems in AP Physics.
📊 Applying Equations to Free Fall and Projectile Motion
The sixth paragraph demonstrates the application of the previously introduced equations to solve problems involving free fall and projectile motion. It provides a detailed explanation of how to use the equations to find displacement and other quantities of interest, such as the number of floors fallen or the speed of an object upon impact. The paragraph also addresses common misconceptions about the relationship between horizontal and vertical motion, emphasizing the importance of understanding the separate components of motion in two-dimensional scenarios.
🎯 Determining Center of Mass and Acceleration in a Two-Ball System
The seventh paragraph discusses the concept of the center of mass and how to calculate it for a system of two balls. It explains the formula for finding the center of mass and provides an example with two rectangles of different masses. The paragraph then applies this concept to a scenario where two balls are dropped and rolled simultaneously, and it asks for the acceleration of the system's center of mass. The explanation includes how to calculate the horizontal and vertical components of acceleration and how they combine to give the overall acceleration.
🔍 Measuring Velocity and Acceleration with Tools
The eighth paragraph discusses the use of photogates and motion detectors for measuring velocity, position, and acceleration of moving objects. It clarifies which tools are suitable for different types of measurements and emphasizes the importance of proper orientation relative to the object's motion. The paragraph also addresses a scenario where a battery-powered toy is tested for constant speed, and it identifies the appropriate measuring tools for such an experiment.
🏆 Testing the Validity of a Toy's Constant Speed Claim
The ninth paragraph presents a scenario where students must design an experiment to test the claim that a battery-powered toy operates at a constant speed. It explains the use of photogates and motion detectors in such an experiment and provides a step-by-step approach to measuring the toy's velocity and determining whether the speed is indeed constant. The paragraph also discusses how to calculate the initial speed of a ball thrown vertically upward and how to determine the total distance traveled by the ball.
📐 Analyzing Motion on a Horizontal Track
The tenth paragraph discusses the analysis of an object's motion along a horizontal track, using a velocity-time graph to determine the object's displacement. It explains how to calculate the area under the graph to find the displacement and how to interpret the graph to understand the object's acceleration. The paragraph also addresses a scenario involving two blocks tied together and sliding across an icy surface, spinning around their center of mass, and it provides insights into the system's total displacement and acceleration.
🌟 Understanding Constant Acceleration and Free Fall
The eleventh paragraph focuses on experiments that demonstrate constant acceleration, specifically in the context of free fall. It identifies situations where an object experiences constant gravitational acceleration and explains how to calculate the object's displacement and velocity at different points in time. The paragraph also discusses the motion of a dart and a target, using velocity-time graphs to analyze their vertical displacement and determine the distance between them at the moment of impact.
📉 Displacement and Velocity Analysis for Various Motion Scenarios
The twelfth paragraph continues the analysis of displacement and velocity for different motion scenarios, including a rock in free fall and an object sliding on a horizontal surface. It explains how to use velocity-time graphs to determine the total distance traveled and the total displacement of an object. The paragraph also addresses the motion of a bowling pin thrown vertically upward and how to calculate its maximum height. Additionally, it covers the displacement of a cart on a horizontal track using a velocity-time graph.
🔄 Center of Mass Velocity and Acceleration in a Rotating System
The thirteenth paragraph discusses the velocity and acceleration of a system's center of mass when two blocks are tied together and thrown onto an icy surface, spinning around their center of mass. It explains how to interpret the velocity-time graph to determine the system's acceleration and the displacement of the individual blocks. The paragraph clarifies that the total displacement of the system's center of mass is not zero and that the acceleration is constant and opposite to the velocity vector.
Mindmap
Keywords
💡Kinematics
💡Displacement
💡Velocity
💡Acceleration
💡Free Fall
💡Projectile Motion
💡Vector Quantities
💡Position-Time Graph
💡Velocity-Time Graph
Highlights
Eugene, a UCLA Grant academic coach, professional tutor, and digital creator, provides free educational content on YouTube.
The focus of the session is on Unit 1 of AP Physics 1, Kinematics, which studies the motion of objects without investigating the causes.
Kinematics covers essential concepts such as displacement, velocity, and acceleration, all of which are vector quantities.
Displacement differs from distance in that displacement considers only the initial and final positions, not the path taken.
Velocity is the instantaneous rate of change in displacement and is a vector quantity, unlike speed, which is a scalar.
Acceleration measures how quickly velocity changes and is represented by the change in velocity over time.
The analysis of velocity versus time and displacement versus time graphs is crucial for understanding an object's motion.
In free fall motion, an object is solely under the influence of gravitational force, leading to a constant acceleration of 9.8 m/s^2.
Projectile motion involves both horizontal and vertical components of motion, with the horizontal component remaining constant.
The path of projectile motion is parabolic because the horizontal velocity is constant while the vertical velocity changes due to gravity.
Eugene provides equations for calculating motion parameters, such as final velocity, position, and acceleration, assuming constant acceleration.
Understanding the difference between speeding up/slowing down and accelerating/decelerating is essential, as they refer to speed and velocity, respectively.
The motion of objects can be analyzed using graphs, with the slope representing velocity and acceleration.
Eugene demonstrates how to calculate the area under a velocity-time graph to find displacement.
The concept of constant acceleration is crucial for solving physics problems, meaning both magnitude and direction remain unchanged.
Eugene explains how to determine the center of mass for a system of two objects and how it relates to the system's motion.
The session covers the application of kinematics equations to real-world scenarios, such as a ball falling from rest.
Eugene addresses common misconceptions about motion, such as the belief that horizontal motion affects the time taken to reach the ground in free fall.
The session concludes with a practical application of kinematics, showing how to use the equations to solve for an object's displacement and velocity.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: