How do you simplify trigonometric expressions
TLDRThe video script provides a comprehensive guide on simplifying trigonometric expressions, emphasizing the importance of using algebraic properties and trigonometric identities. It starts by highlighting the reciprocal property, which allows for the simplification of expressions by dividing out common terms. The script then delves into factoring, particularly the difference of two squares, and the use of the AC method. It stresses the significance of applying trigonometric identities to transform expressions into simpler forms, such as using the quotient identity to combine tangent and cosine functions. The video also encourages looking for opportunities to apply Pythagorean identities, especially when terms are squared, to further simplify expressions. Lastly, it advises on algebraic processes like adding and subtracting fractions by finding common denominators. The key takeaway is to apply these mathematical tools iteratively, trying different approaches until the expression is simplified to its most basic form.
Takeaways
- 📚 **Reciprocal Property**: When simplifying trigonometric expressions, look for opportunities to use reciprocal properties to cancel out terms and simplify expressions.
- 🔢 **Order of Operations**: Apply the order of operations (similar to algebraic expressions) to simplify trigonometric expressions step by step.
- ✅ **Factoring**: Factor expressions, especially looking for patterns like the difference of two squares, to simplify further.
- 🔁 **Trigonometric Identities**: Utilize known trigonometric identities to substitute and simplify expressions, such as quotient, cofunction, and even-odd identities.
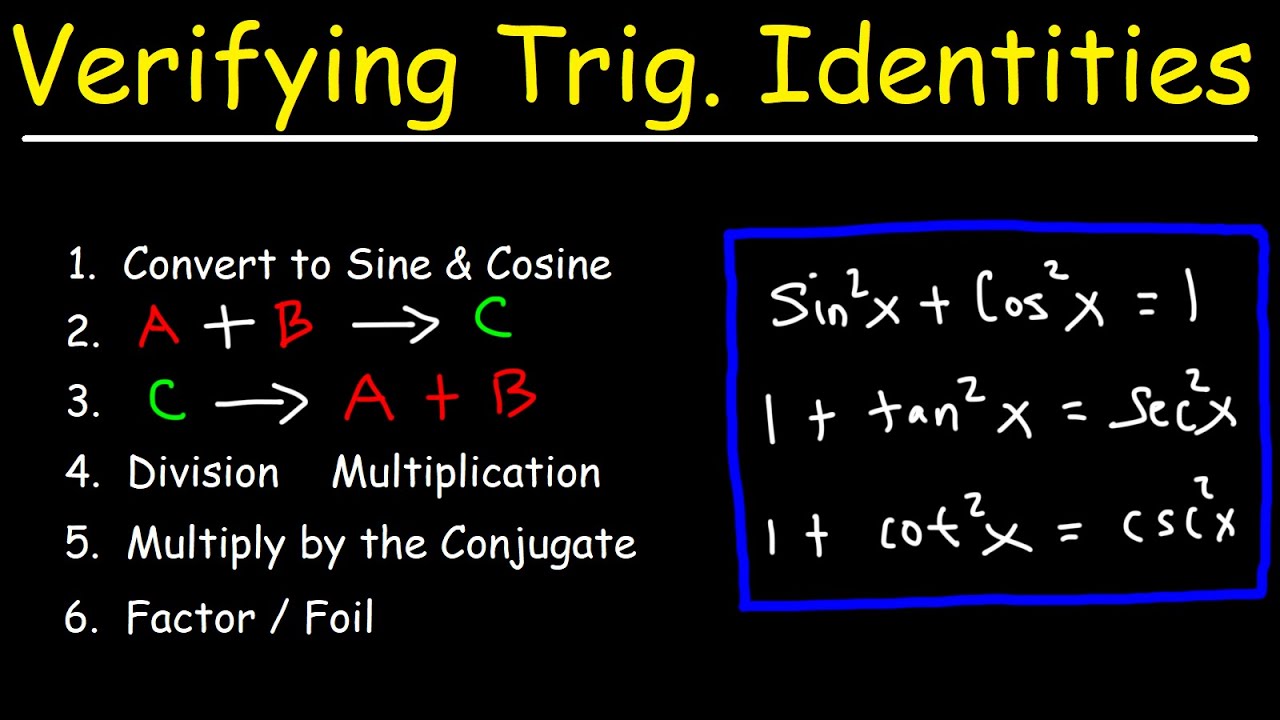
- 🔄 **Simplifying with Pythagorean Identity**: Recognize when to apply the Pythagorean identity (sin²x + cos²x = 1) to terms that are squared to simplify the expression.
- 🔍 **Looking for Patterns**: Keep an eye out for patterns like sin²x, cos²x, or tan²x, which can often be simplified using trigonometric identities.
- 🧩 **Combining Terms**: When adding or subtracting, ensure common denominators to combine terms effectively.
- 📉 **Sine and Cosine Relationships**: Use the relationship between sine and cosine (as in tangent) to simplify expressions by canceling out terms.
- 🎯 **Trial and Error**: Don't be afraid to try different approaches; if one method doesn't work, try substituting a different identity.
- ⚖️ **Algebraic Processes**: Employ algebraic processes like multiplying, dividing, adding, and subtracting to simplify trigonometric expressions.
- 📈 **Simplify to the Basics**: Aim to simplify expressions to their most basic form, often involving one or two trigonometric functions at most.
Q & A
What is the general approach to simplifying trigonometric expressions?
-The general approach to simplifying trigonometric expressions involves using properties similar to those used in simplifying algebraic expressions, such as the order of operations. The goal is to simplify the expression to its simplest form, often by reducing it to a single trigonometric function or a numerical value.
What is the reciprocal property in the context of trigonometric expressions?
-The reciprocal property allows you to simplify expressions by dividing out common terms. For instance, if you have an expression like x/y * 1/x, you can simplify it to 1/y after canceling out the x terms.
How can you simplify expressions involving complex fractions?
-For complex fractions, you can multiply by the reciprocal of the denominator to simplify the expression. This process cancels out the denominator, leaving you with a simpler fraction.
What role does factoring play in simplifying trigonometric identities?
-Factoring is crucial in simplifying trigonometric identities. It allows you to break down expressions into simpler components, which can then be more easily manipulated and reduced using trigonometric identities.
What is the quotient identity and how is it used in simplifying trigonometric expressions?
-The quotient identity is a relationship between the tangent function and the sine and cosine functions, expressed as tangent(θ) = sine(θ) / cosine(θ). It is used to rewrite expressions in terms of sines and cosines, which can then be simplified by canceling out common terms.
What are the main trigonometric identities that should be applied when simplifying expressions?
-The main trigonometric identities to apply include the quotient identity, cofunction identities, and even-odd identities. These are used to substitute and simplify expressions, often resulting in a more manageable form.
Why is it beneficial to look for terms of sine squared or cosine squared in a trigonometric expression?
-Looking for terms of sine squared or cosine squared is beneficial because they can often be replaced with the Pythagorean identity, which states that sine squared(θ) + cosine squared(θ) = 1. This substitution can simplify the expression and make it easier to solve.
How can you create opportunities to use the Pythagorean identity in a trigonometric expression?
-You can create opportunities to use the Pythagorean identity by manipulating the denominator to include terms like cosine squared(θ) - 1, which can then be rewritten using the identity sine squared(θ) + cosine squared(θ) = 1.
What is the significance of finding a common denominator when adding fractions in trigonometric expressions?
-Finding a common denominator is essential for adding fractions because it allows you to combine the fractions into a single expression with a consistent denominator, which can then be more easily simplified.
What are some algebraic processes that can be used in conjunction with trigonometric identities to simplify expressions?
-Algebraic processes such as multiplying, dividing, adding, and subtracting can be used alongside trigonometric identities. Factoring is particularly useful for breaking down complex expressions into simpler forms that can be further simplified.
What is the final advice given for approaching the simplification of trigonometric expressions?
-The final advice is to start by trying different approaches and applying the relevant trigonometric identities. If one method doesn't work, try another identity or approach until you reach the simplest form of the expression.
Outlines
📚 Simplifying Trigonometric Expressions
This paragraph introduces the process of simplifying trigonometric expressions, drawing parallels to the simplification of algebraic expressions. It emphasizes the importance of using trigonometric properties and identities to reduce complex expressions to simpler forms. The concept of reciprocal properties is discussed, explaining how to simplify rational expressions by canceling out terms. The paragraph also touches on factoring techniques and the use of trigonometric identities, particularly focusing on quotient and cofunction identities, to further simplify expressions. The goal is to arrive at a final answer that is either a number or a simplified function of one or two trigonometric terms.
🔢 Applying Identities and Factoring in Trigonometry
This paragraph delves deeper into the application of trigonometric identities and factoring techniques in simplifying expressions. It highlights the importance of recognizing opportunities to use identities and the Pythagorean identity in particular, to transform squared trigonometric terms. The paragraph also discusses the strategy of creating expressions that can be simplified using identities, such as sine squared or cosine squared, and the process of factoring the difference of squares. Additionally, it touches on algebraic processes like finding common denominators for addition and the importance of trying different approaches to arrive at the simplest form of a trigonometric expression.
Mindmap
Keywords
💡Simplifying
💡Trigonometric Expressions
💡Reciprocal Property
💡Factoring
💡Trigonometric Identities
💡Pythagorean Identity
💡Quotient Identity
💡Algebraic Processes
💡Common Denominators
💡Sine and Cosine Functions
💡Tangent Function
Highlights
The process of simplifying trigonometric expressions is similar to simplifying numeric and algebraic expressions using order of operations.
Simplifying involves reducing complex expressions to their simplest form, often using a single or a combination of one or two functions.
Reciprocal properties are essential, allowing the division of trigonometric terms to equal one.
When dealing with fractions, always look for opportunities to divide out terms to simplify expressions.
Factoring is a key skill, especially factoring the difference of two squares and using the AC method.
Trigonometric identities are crucial for substitution into equations to simplify expressions.
Quotient and reciprocal identities are the main functions to use in almost every problem.
Cofunction identities and even-odd identities are also important for simplification.
When simplifying, it's about trying different approaches and identities to see what works best.
Look for terms like sine squared or cosine squared and use the Pythagorean identity to simplify.
Creating sine squared and cosine squared terms can help in applying Pythagorean identities.
When adding fractions, ensure you have common denominators to combine terms effectively.
Applying algebraic processes such as multiplying, dividing, adding, and subtracting is key to simplification.
Always be on the lookout for opportunities to use factoring to simplify trigonometric expressions.
The goal is to apply identities and algebraic processes to simplify expressions as much as possible.
There's no one-size-fits-all answer; the process involves trial and error with different identities and methods.
The process of simplification is iterative, trying different approaches until the expression is as simplified as it can be.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: