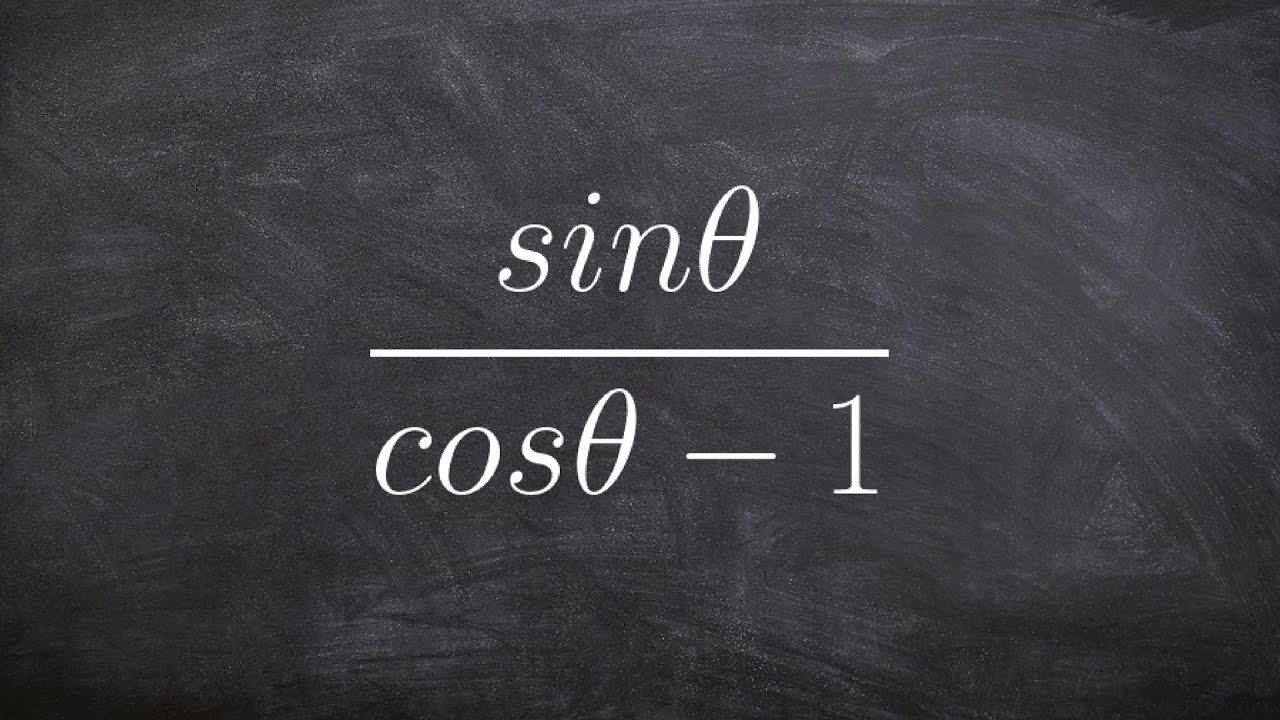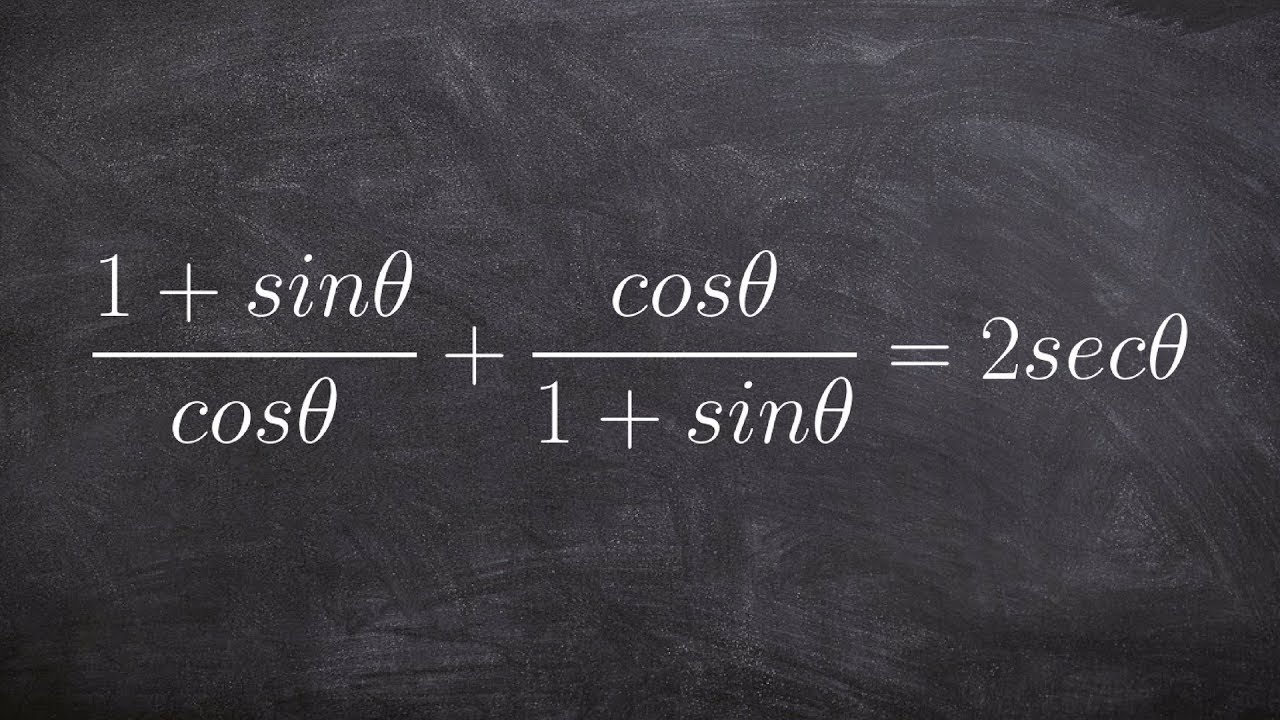Ex 2: Simplify Trigonometric Expressions

Mathispower4u
29 Jun 201206:25
EducationalLearning
32 Likes 10 Comments

TLDRThis instructional video script guides viewers through simplifying trigonometric expressions using identities and algebraic manipulation. It begins by converting all trig functions to sine and cosine, then demonstrates how to find a common denominator to subtract fractions. The script uses the Pythagorean identity to substitute terms and simplify the expression to a single trig function. The first example simplifies to cosine theta, while the second simplifies to cosecant theta. The process is detailed, aiming to help viewers understand the steps involved in simplifying complex trigonometric expressions.

Takeaways
  • 📚 The goal is to simplify trigonometric expressions by converting them into a single trigonometric function.
  • 🔍 The script uses trigonometric identities to simplify expressions, starting with converting all functions to sine and cosine.
  • 📐 The process involves converting cosecant to 1/sin(θ) and cotangent to cos(θ)/sin(θ) to facilitate simplification.
  • 🧩 In the first example, a common denominator of sin(θ) is introduced to subtract fractions and simplify the expression.
  • 🔄 The Pythagorean identity 1 - sin²(θ) = cos²(θ) is used to substitute and simplify the expression further.
  • 📉 The script shows that multiplying by the reciprocal of a fraction can simplify division problems into multiplication.
  • 📈 After simplification, the first example results in the expression cos²(θ)/sin(θ), which simplifies to cos(θ).
  • 🔄 For the second expression, the process is similar, converting all functions to sine and cosine and finding a common denominator.
  • 📉 The second example uses the identity 1 - cos²(θ) = sin²(θ) to simplify the expression.
  • 📈 The final result of the second expression simplifies to 1/sin(θ), which is cosecant theta (csc(θ)).
  • 🔑 The script emphasizes the importance of using trigonometric identities and algebraic manipulation to simplify expressions.
Q & A

  • What is the main goal of simplifying trigonometric expressions?

    -The main goal of simplifying trigonometric expressions is to rewrite the expression in terms of a single trigonometric function, making it easier to understand and work with.

  • Why is it necessary to convert all trigonometric functions to sines and cosines when simplifying?

    -Converting all trigonometric functions to sines and cosines is necessary because these are the most fundamental trigonometric functions, and it allows for the use of basic trigonometric identities to simplify the expression.

  • What is the reciprocal of cosecant in terms of sine?

    -The reciprocal of cosecant is sine, as cosecant theta is equal to 1 divided by sine theta.

  • How does the script suggest simplifying the expression involving cotangent and cosecant?

    -The script suggests converting cotangent and cosecant to sine and cosine, finding a common denominator, and then subtracting the fractions to simplify the expression.

  • What is the common denominator used when simplifying the first example in the script?

    -The common denominator used when simplifying the first example is sine theta.

  • How can the Pythagorean identity help in simplifying the expression 1 - sine squared theta?

    -The Pythagorean identity can be used to express 1 - sine squared theta as cosine squared theta, since cosine squared theta is equal to 1 minus sine squared theta.

  • What is the result of the first trigonometric expression simplification in the script?

    -The result of the first trigonometric expression simplification is cosine theta.

  • What is the reciprocal of secant in terms of cosine?

    -The reciprocal of secant is cosine, as secant theta is equal to 1 divided by cosine theta.

  • How does the script suggest simplifying the second expression involving tangent, secant, and cosine?

    -The script suggests converting tangent and secant to sine and cosine, finding a common denominator, and then using the identity for sine squared theta to simplify the expression.

  • What is the result of the second trigonometric expression simplification in the script?

    -The result of the second trigonometric expression simplification is cosecant theta.

  • Why is it helpful to express division as multiplication by the reciprocal when simplifying trigonometric expressions?

    -Expressing division as multiplication by the reciprocal simplifies the process by allowing us to cancel out common factors and makes it easier to see how the expression can be simplified.

Outlines
00:00
📚 Simplifying Trigonometric Expressions Using Identities

This paragraph discusses the process of simplifying trigonometric expressions by converting them into a single trigonometric function using given identities. The focus is on converting cosecant, sine, and cotangent to sine and cosine functions and then simplifying the resulting fractions. The Pythagorean identities are used to transform the expression into a form that allows for simplification. The example provided walks through converting 1 - sine squared theta into cosine squared theta, and then simplifying the expression to a single cosine function of theta.

05:06
🔍 Further Simplification of Trigonometric Expressions

The second paragraph continues the theme of simplifying trigonometric expressions. It starts by converting tangent and secant to sine and cosine, and then proceeds to simplify the expression by finding a common denominator. The goal is to express the entire fraction in terms of sine and cosine. The paragraph demonstrates the use of the Pythagorean identity to replace 1 - cosine squared theta with sine squared theta. The final step involves converting the division problem into a multiplication one, simplifying the expression to cosecant theta, thus completing the simplification process.

Mindmap
Keywords
💡Simplify
To 'simplify' in the context of trigonometry means to reduce a trigonometric expression to a more straightforward form, often involving fewer terms or a single trigonometric function. In the video, the main theme revolves around simplifying complex trigonometric expressions, such as converting all terms to sines and cosines, which is a common strategy in trigonometric simplification.
💡Trigonometric Identities
Trigonometric Identities are equations that hold true for all values of the variables involved and are used to simplify trigonometric expressions. In the script, identities such as the Pythagorean identities are highlighted as crucial tools for simplifying the given trig expressions, by allowing substitutions that make the expressions more manageable.
💡Cosecant
Cosecant (csc) is a reciprocal trigonometric function defined as the reciprocal of sine (csc(θ) = 1/sin(θ)). In the video, cosecant is one of the functions that the expression is initially in, and it is later converted to sines and cosines as part of the simplification process.
💡Sine
Sine (sin) is a fundamental trigonometric function that relates the ratio of the opposite side to the hypotenuse in a right-angled triangle. The script uses sine as a base function to which other trigonometric functions are converted during the simplification process.
💡Cotangent
Cotangent (cot) is another reciprocal trigonometric function, defined as the reciprocal of tangent (cot(θ) = 1/tan(θ) = cos(θ)/sin(θ)). In the video, cotangent is initially present in the expression and is then expressed in terms of sine and cosine to aid in simplification.
💡Common Denominator
A 'common denominator' is a single denominator that is shared by two or more fractions, allowing for the addition or subtraction of these fractions. In the script, finding a common denominator is a necessary step in the process of combining fractions with different denominators, such as sine and cosine, to simplify the expression.
💡Pythagorean Identities
Pythagorean Identities relate the squares of the sine and cosine of an angle to 1 (sin²(θ) + cos²(θ) = 1). These identities are used in the video to make substitutions that help simplify the trigonometric expression by converting it into a form that can be more easily reduced.
💡Cosine
Cosine (cos) is a trigonometric function that, like sine, relates to the sides of a right-angled triangle, specifically the ratio of the adjacent side to the hypotenuse. The script demonstrates the use of cosine in the simplification process, showing how it can be manipulated to achieve a simpler form.
💡Tangent
Tangent (tan) is a trigonometric function defined as the ratio of the opposite side to the adjacent side in a right-angled triangle (tan(θ) = sin(θ)/cos(θ)). In the script, tangent is converted to sine and cosine as part of the simplification strategy for the trigonometric expression.
💡Secant
Secant (sec) is the reciprocal of the cosine function (sec(θ) = 1/cos(θ)). The script mentions secant as part of the original expression that needs to be simplified, and it is later expressed in terms of cosine to facilitate the simplification process.
💡Reciprocal
A 'reciprocal' of a number is what you multiply by that number to get 1 (e.g., the reciprocal of cos(θ) is 1/cos(θ)). In the video, the concept of reciprocals is used to transform division problems into multiplication problems, which simplifies the process of combining fractions.
Highlights

The objective is to simplify trigonometric expressions using identities.

Conversion of all terms to sines and cosines is the initial approach.

Cosecant theta is expressed as 1 divided by sine theta.

Sine theta is rewritten as a fraction to facilitate subtraction.

Cotangent theta is converted to cosine theta divided by sine theta.

Subtraction of fractions requires a common denominator, which is sine theta.

The process involves multiplying fractions to achieve a common denominator.

The numerator simplifies to 1 minus sine squared theta.

Pythagorean identities are used for substitution involving sine squared theta.

Cosine squared theta is substituted for 1 minus sine squared theta.

The expression is rewritten as a division problem involving trigonometric functions.

Division is converted to multiplication by using the reciprocal.

Factors of cosine theta simplify, leaving a single factor.

The final simplified form of the first expression is cosine theta.

The second expression also starts with converting all terms to sines and cosines.

Tangent theta is expressed as sine theta divided by cosine theta.

Secant theta is converted to 1 divided by cosine theta.

A common denominator of cosine theta is used for subtraction.

The numerator becomes 1 minus cosine squared theta after simplification.

Sine squared theta is substituted for 1 minus cosine squared theta using identities.

The expression is transformed into a multiplication problem for simplification.

Factors simplify to leave a single factor of sine theta.

The final simplified form of the second expression is cosecant theta.

Transcripts

Browse More Related Video

Verifying trigonometric identities, hard with multiple steps

Identities Grade 11: Introduction and practice

How do you simplify trigonometric expressions

Proving Trigonometric Identities (Part 2) (5.5)

Verifying a trigonometric Identities

Ultimate trig identity problem study guide!

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometrySimplificationPythagorean IdentitiesMath TutorialTrig FunctionsEducational ContentMathematicsFractional TermsSine and CosineTrig Identities