Optimization: profit | Applications of derivatives | AP Calculus AB | Khan Academy

Khan Academy
31 Jan 201311:26
EducationalLearning
32 Likes 10 Comments

TLDRIn the video script, the presenter discusses optimizing profit for a shoe factory by determining the optimal number of thousands of pairs to produce. They introduce a revenue function based on a wholesaler's offer and a cost function provided by consultants. Using calculus, the presenter finds critical points to maximize profit, solving a quadratic equation for x and applying the second derivative test to confirm a maximum profit point at 3,528 pairs, resulting in a profit of $13,128.

Takeaways
  • πŸ‘Ÿ The script discusses the optimization of profit for a shoe factory by determining the optimal number of thousands of pairs of shoes to produce.
  • πŸ“ˆ The revenue function is given as 10 times x, where x represents thousands of pairs of shoes produced, and revenue is in thousands of dollars.
  • πŸ’° The cost function is a cubic function of x, which includes terms for the cube, square, and linear components of the number of shoes produced, also in thousands of dollars.
  • πŸ” Profit is calculated by subtracting the cost function from the revenue function, aiming to find the maximum profit point.
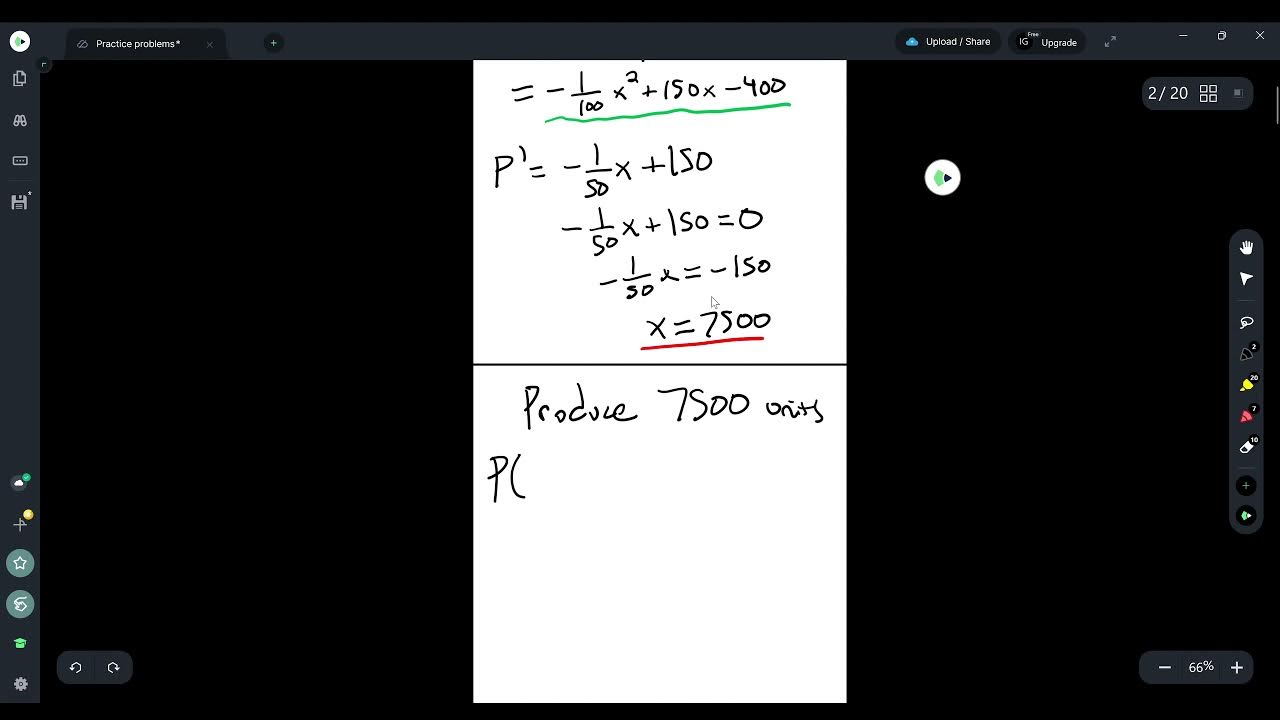
  • πŸ“š The critical points of the profit function are found by setting its first derivative equal to zero, which simplifies to solving a quadratic equation.
  • πŸ”’ The quadratic formula is used to find the potential critical points, resulting in two possible values for x.
  • πŸ“‰ The second derivative test is applied to determine whether the critical points are maximum or minimum points, using the concavity of the function.
  • πŸ“ˆ The maximum profit point is identified as x = 3.528, indicating the optimal number of thousands of pairs to produce for maximum profit.
  • πŸ’‘ The second derivative at the critical point of 3.528 is negative, indicating that the function is concave down and thus at a maximum there.
  • πŸ“ The profit at the optimal production level (3,528 pairs) is calculated to be approximately $13,128, considering the profit function's value at x = 3.528.
  • πŸš€ The conclusion suggests that by producing 3,528 pairs of shoes, the shoe factory can achieve a profit of $13,128, optimizing their financial outcome.
Q & A

  • What is the main objective of the shoe factory owner in the script?

    -The main objective of the shoe factory owner is to determine the optimal number of thousands of pairs of shoes to produce in order to maximize profit.

  • What is the revenue function for the shoe factory as described in the script?

    -The revenue function is given by 10 times x, where x represents the thousands of pairs of shoes produced.

  • What are the components of the cost function for the shoe factory?

    -The cost function is composed of the cube of the thousands of pairs produced, minus 6 times the square of the thousands of pairs produced, plus 15 times the thousands of pairs produced.

  • How is the profit function derived from the revenue and cost functions?

    -The profit function is derived by subtracting the cost function from the revenue function, which is represented as 10x minus (x^3 - 6x^2 + 15x).

  • What is the first step in optimizing the profit function?

    -The first step in optimizing the profit function is to find the critical points, which are determined by setting the first derivative of the profit function equal to zero.

  • What is the first derivative of the profit function?

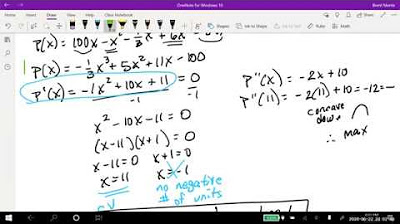
    -The first derivative of the profit function is -3x^2 + 12x - 5.

  • How does one determine whether a critical point is a maximum, minimum, or neither?

    -The second derivative test is used to determine the nature of a critical point. If the second derivative at a critical point is less than 0, it indicates a maximum; if greater than 0, it indicates a minimum.

  • What is the second derivative of the profit function?

    -The second derivative of the profit function is -6x + 12.

  • What are the critical points calculated for the profit function in the script?

    -The critical points calculated are approximately 3.528 and 0.4725, which represent thousands of pairs of shoes.

  • How does the script determine the optimal number of shoes to produce for maximum profit?

    -The script uses the second derivative test to determine that the critical point at 3.528 is a maximum, indicating that producing 3,528 pairs of shoes will yield the maximum profit.

  • What is the maximum profit calculated for producing 3,528 pairs of shoes?

    -The maximum profit calculated for producing 3,528 pairs of shoes is approximately $13,128.

Outlines
00:00
πŸ‘Ÿ Starting a Shoe Factory

This paragraph introduces the scenario of opening a shoe factory and the challenge of determining the optimal production quantity for maximizing profit. It defines 'x' as the thousands of pairs of shoes produced and explains how to calculate revenue, given a wholesaler willing to pay $10 per pair. It also discusses the costs involved, including materials, factory construction, and operational expenses, which are expressed as a cubic function of x. The goal is to optimize profit, defined as revenue minus cost, through an analytical approach.

05:01
πŸ“ˆ Solving for Critical Points

The paragraph continues with the mathematical process of finding critical points of the profit function by setting its first derivative to zero. The quadratic formula is used to solve for x, resulting in two critical points: approximately 3.528 and 0.4725. These represent potential maximum and minimum points for profit. Calculations for both points are shown to determine their values.

10:02
πŸ” Analyzing Concavity

This paragraph applies the second derivative test to determine the nature of the critical points. By evaluating the second derivative at 3.528 and 0.4725, it is concluded that the function is concave downwards at 3.528 (indicating a maximum) and concave upwards at 0.4725 (indicating a minimum). Hence, producing 3.528 thousand pairs of shoes (or 3,528 pairs) is optimal for maximizing profit.

Mindmap
Keywords
πŸ’‘Revenue
Revenue refers to the total income that a company generates from its business activities, usually from the sale of goods or services. In the video's context, the revenue function is defined as 10 times x, where x represents the thousands of pairs of shoes produced. The script uses the revenue function to illustrate how the income from shoe sales is directly proportional to the quantity produced, with $10,000 being the revenue for producing 1,000 pairs of shoes.
πŸ’‘Cost
Cost is the expense incurred in the production of goods or services, including materials, labor, and overhead. The script introduces a cost function that is a cubic polynomial in terms of x, reflecting the costs associated with producing x thousands of pairs of shoes. This cost function is crucial for understanding the business's expenses and how they scale with production levels.
πŸ’‘Profit
Profit is the difference between a company's revenue and its costs, indicating the financial gain or loss from its operations. The video's theme revolves around optimizing profit, which is calculated by subtracting the cost function from the revenue function. The script demonstrates the process of finding the production quantity that maximizes profit through mathematical optimization.
πŸ’‘Critical Points
Critical points in calculus are the values of the independent variable where the derivative of a function is either zero or undefined. The script discusses finding the critical points of the profit function to determine potential maximum or minimum profit levels. The critical points are calculated by setting the first derivative of the profit function equal to zero.
πŸ’‘Derivative
A derivative in calculus represents the rate of change of a function with respect to its variable. The script uses the derivative of the profit function to find the critical points, which are essential for optimization. The first derivative of the profit function is calculated and set to zero to find the points where the profit could be maximized or minimized.
πŸ’‘Quadratic Formula
The quadratic formula is used to solve quadratic equations of the form ax^2 + bx + c = 0. In the script, after simplifying the equation for the critical points, the quadratic formula is applied to find the values of x that make the first derivative of the profit function equal to zero, which are potential optimal production quantities.
πŸ’‘Second Derivative Test
The second derivative test is a method used to determine the concavity of a function and to identify local maxima and minima. The script applies this test by evaluating the second derivative of the profit function at the critical points to ascertain whether they correspond to maximum or minimum profit levels.
πŸ’‘Concave Upwards/Downwards
A function is said to be concave upwards if its second derivative is positive over an interval, indicating that the function is bending upwards. Conversely, it is concave downwards if the second derivative is negative, bending downwards. The script uses these concepts to analyze the shape of the profit function around the critical points and to determine whether they represent maximum or minimum profits.
πŸ’‘Optimization
Optimization in the context of the video refers to the process of finding the best possible solution to a problem, such as maximizing profit. The script demonstrates the mathematical process of optimization by using derivatives and the second derivative test to find the production quantity that yields the highest profit.
πŸ’‘Wholesaler
A wholesaler is a person or company that buys goods in large quantities directly from producers and sells them to retailers or other merchants. In the script, the wholesaler is willing to pay $10 per pair of shoes, which sets the revenue per pair of shoes produced by the factory.
πŸ’‘Cubic Polynomial
A cubic polynomial is a polynomial of degree three, having the general form ax^3 + bx^2 + cx + d. The script introduces a cost function that is a cubic polynomial, where the coefficients and variables represent the costs associated with different levels of shoe production.
Highlights

Introduction of the problem: optimizing profit for a shoe factory by determining the optimal number of thousands of pairs to produce.

Definition of x as the thousands of pairs of shoes produced.

Explanation of revenue function: revenue as a function of x, with a wholesaler willing to pay $10 per pair.

Calculation of revenue: 10x, where x is in thousands of pairs, translating to thousands of dollars.

Introduction of costs: materials, factory, employees, and electricity.

Cost function provided by consultants: cost as a function of x is x^3 - 6x^2 + 15x.

Definition of profit: profit as a function of x is revenue minus cost.

Simplification of the profit function: p(x) = 10x - (x^3 - 6x^2 + 15x) = -x^3 + 6x^2 - 5x.

Introduction of critical points: finding the derivative of the profit function to determine maximum and minimum points.

Calculation of the first derivative: p'(x) = -3x^2 + 12x - 5.

Solving for critical points: setting the first derivative to zero and solving the quadratic equation.

Calculation using the quadratic formula: x = 3.528 and x = 0.4725 as critical points.

Introduction of the second derivative test: p''(x) = -6x + 12.

Determination of concavity: p''(3.528) < 0 indicating a maximum, and p''(0.4725) > 0 indicating a minimum.

Calculation of maximum profit: substituting x = 3.528 back into the profit function yields a profit of approximately $13,128.

Transcripts

Browse More Related Video

Optimization Problem Examples

Math 11 - Section 3.5

BusCalc 10 Marginal Profit

Business Applications of Extrema

Marginal Revenue, Average Cost, Profit, Price & Demand Function - Calculus

Marginal Cost, Marginal Revenue, and Marginal Profit

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Profit OptimizationShoe FactoryMathematical ModelingCritical PointsRevenue FunctionCost FunctionDerivative AnalysisQuadratic EquationBusiness StrategyEconomic MaximizationProduction Planning