Limits at Infinity (Rational square-root function as x approaches negative Infinity)
TLDRIn this educational video, the host, Newton, introduces the concept of negative numbers in the context of square roots and limits. He explains that the square root of a number can yield both positive and negative results, depending on the situation. The video delves into solving limits as x approaches negative infinity, emphasizing the importance of considering the negative sign when taking the square root. Newton demonstrates a step-by-step method for dividing expressions and simplifying them to find the limit, ultimately concluding that the limit of the given function as x approaches negative infinity is negative three. The video encourages continuous learning and critical thinking in mathematics.
Takeaways
- 📌 The video introduces the concept of negative side in the context of square roots and its importance in determining the sign of the result.
- 📈 When taking the square root of a number, the result can be both positive and negative, but the sign depends on the context, such as x approaching negative infinity.
- 🔢 The example given is the square root of 9, which is not just 3, but ±3, highlighting the need to consider the scenario when determining the sign.
- 📚 The video emphasizes the importance of creating rational terms to facilitate the division by infinity, which results in the answer being zero.
- 🛑 A reminder to avoid having zero under and zero on top, as this would lead to an undefined result.
- 🔍 The process of dividing by the highest denominator is explained to simplify the problem and avoid undefined expressions.
- 🌐 The video demonstrates how to break up the denominator in algebra, but emphasizes that certain expressions, like those under a square root sign, are bound together and require special handling.
- 📝 The method of pushing a number under a square root sign by squaring it is discussed, which simplifies the expression and allows for easier computation.
- 📊 The concept of negative infinity and its impact on the square root is clarified, reinforcing that the square root of a number when x is negative should result in a negative number.
- 📈 The final calculation shows that the limit of the function as x approaches negative infinity is negative three, providing a clear conclusion to the problem discussed.
- 💡 The video ends with an encouragement to continue learning, emphasizing that learning is essential for growth and understanding.
Q & A
What is the main topic of the video?
-The main topic of the video is about understanding the concept of negative side when taking the square root of a number, especially in the context of limits as a variable approaches negative infinity.
Why is the negative sign important when taking the square root of a number in this context?
-The negative sign is important because it indicates that when the variable is approaching negative infinity, the result of the square root should also be negative, reflecting the nature of the numbers being dealt with in the limit.
How does the speaker suggest to handle the square root of 9 in the context of limits?
-The speaker suggests that instead of just thinking the square root of 9 is 3, one should consider it as the absolute value of 3, meaning it could be either positive 3 or negative 3, depending on the situation. When x is approaching negative infinity, the square root should be negative.
What is the significance of creating rational terms in the problem?
-Creating rational terms is significant because it allows the introduction of infinity into the equation. This helps in getting a result of zero when something is divided by infinity, which is a common technique used in evaluating limits.
How does the speaker simplify the expression with the highest denominator?
-The speaker simplifies the expression by dividing both the numerator and the denominator by the highest denominator, which in this case is x to the sixth power. This is done to avoid having zero under and zero on top, which would result in an undefined expression.
What is the purpose of breaking up the denominator in the given example?
-Breaking up the denominator into separate terms allows for further simplification of the expression. It makes it possible to cancel out terms and to focus on the relevant parts of the expression when evaluating the limit.
How does the speaker handle the square root sign when trying to simplify the expression?
-The speaker suggests that to simplify the expression under the square root sign, one must 'sneak' the term under the square root by squaring it. This allows the term to be part of the expression under the square root without disrupting the other terms.
What is the final result of the limit as x approaches negative infinity in the given example?
-The final result of the limit as x approaches negative infinity in the given example is negative three. This is because the square root of nine is three, and since x is approaching negative infinity, the result is negative.
What does the speaker advise regarding the sign of the result when x is approaching negative infinity?
-The speaker advises that when x is approaching negative infinity, the sign of the result should be negative. This is because the square root of a number when x is negative should also be negative, reflecting the negative nature of the variable.
What is the speaker's final message about learning?
-The speaker's final message is that one should never stop learning. He uses the phrase 'never stop learning because those who stopped learning, I've stopped living' to emphasize the importance of continuous learning and growth.
Outlines
📚 Introduction to Negative Side Concepts
This paragraph introduces the concept of negative side in mathematical calculations, specifically in the context of square roots. The speaker, Newton, emphasizes the importance of understanding that the square root of a number can have both positive and negative values, depending on the situation. He uses the example of the square root of 9, explaining that it can be either +3 or -3, and highlights how the negative sign becomes crucial when dealing with the square root of a number as x approaches negative infinity. The paragraph also touches on the strategy of creating rational terms to solve problems involving infinity, and the process of dividing by the highest denominator to avoid undefined expressions.
🔢 Dealing with Infinity in Limits
In this paragraph, the speaker continues the discussion on limits by focusing on how to handle situations where x approaches negative infinity. The explanation involves breaking down complex expressions into simpler forms and understanding the behavior of numbers under the square root when dealing with infinity. The speaker corrects a common misconception about the square root of numbers, especially when they are related to negative infinity, and provides a step-by-step method for solving such problems. The paragraph concludes with the calculation that the limit of the given function as x approaches negative infinity is negative three, and a reminder of the importance of continuous learning in mathematics.
Mindmap
Keywords
💡Square Root
💡Negative Infinity
💡Rational Terms
💡Limit
💡Algebra
💡Infinity
💡Polynomial
💡Absolute Value
💡Denominator
💡Context
Highlights
The video introduces the concept of negative side in mathematical calculations.
The importance of the negative sign when taking the square root of a number is discussed.
The video explains that the square root of nine is the absolute value of three, which includes both positive and negative three.
The concept of approaching negative infinity in mathematical problems is introduced.
The method of creating rational terms to introduce infinity for division by infinity problems is presented.
The highest denominator is chosen for division to simplify the problem.
The process of breaking up the denominator in algebraic expressions is discussed.
The technique of pushing a number under the square root sign by squaring it is explained.
The video emphasizes the importance of remembering to include the negative sign when dealing with negative infinity.
The concept of the square root of negative numbers is clarified with examples.
The method of simplifying problems by canceling out terms is demonstrated.
The video explains that dividing anything by infinity results in zero.
The process of substituting infinity into a calculation is detailed.
The conclusion that the limit of a function as x approaches negative infinity is negative three is reached.
The video visually describes the graph approaching negative three without ever reaching it.
The presenter, Newton, encourages continuous learning as a way of life.
The video concludes with a summary that the limit of the function as x approaches negative infinity is negative three.
Transcripts
Browse More Related Video

Limits at infinity of quotients with square roots (even power) | AP Calculus AB | Khan Academy
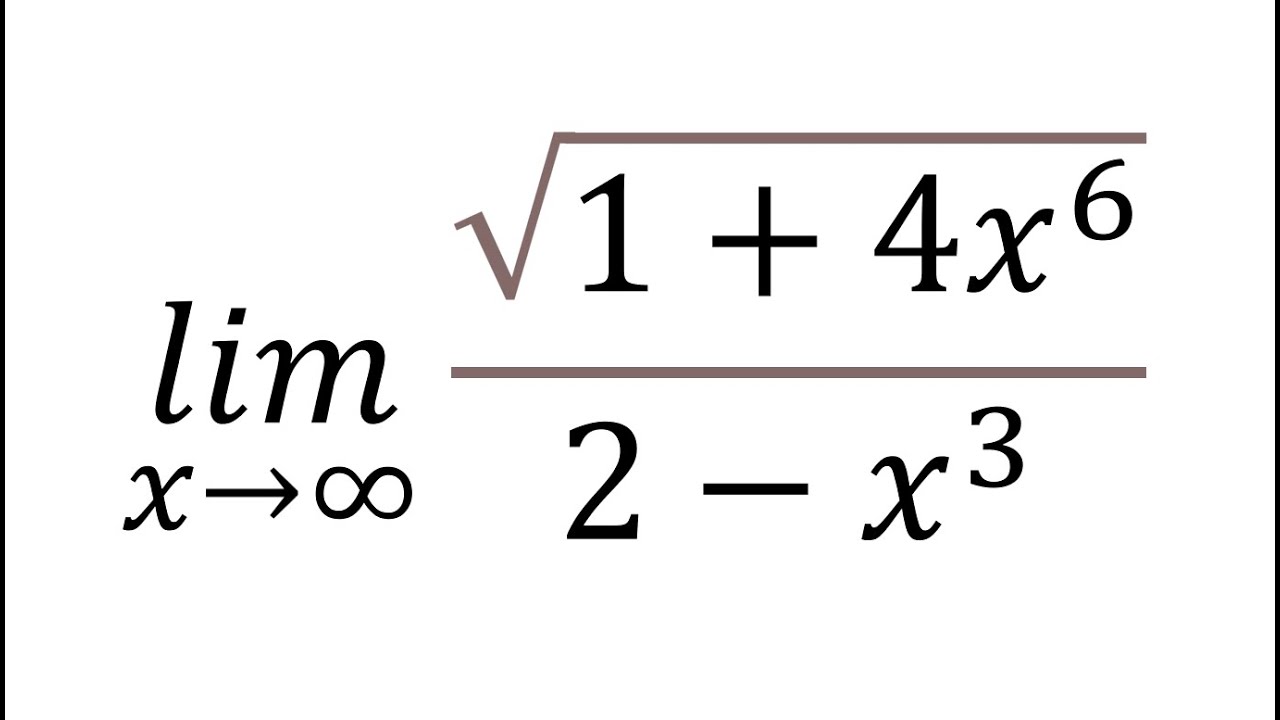
Find limit at Infinity | sqrt(1+4x^6)/(2-x^3) x approaches infinity | general solution

Limits at Infinity & Horizontal Asymptotes
2012 AP Calculus AB Free Response #4

Calculus 1 Lecture 3.5: Limits of Functions at Infinity

Business Calculus - Math 1329 - Section 1.5 (and 1.6) - Limits and Continuity
5.0 / 5 (0 votes)
Thanks for rating: