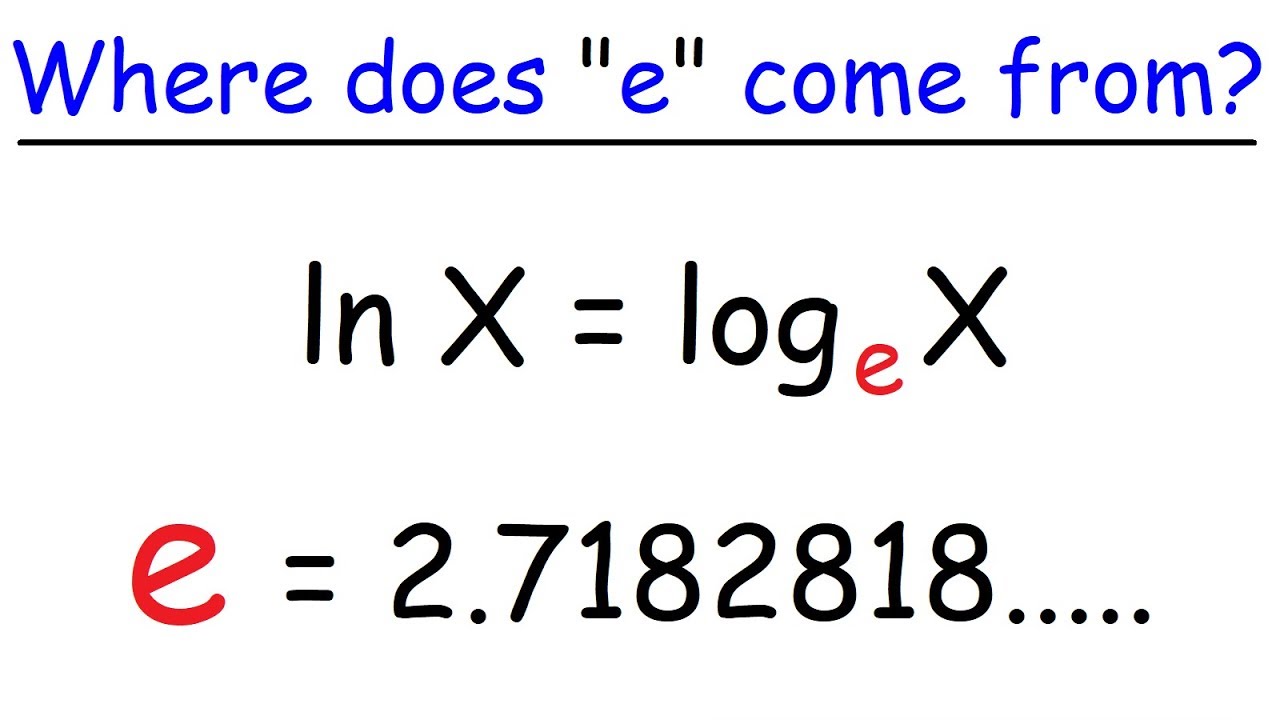The History of the Natural Logarithm - How was it discovered?

Tarek Said

4 Mar 202218:21

EducationalLearning

32 Likes 10 Comments

TLDRThis script delves into the intriguing history of the natural logarithm, revealing its discovery before the number 'e' was known. Initially, logarithms were calculation tables simplifying complex operations. John Napier's invention revolutionized astronomical and navigational calculations. The script explains how logarithms evolved from Napier's artificial numbers to the natural logarithm, which was later connected to the area under the hyperbola and the number 'e' by mathematicians like Euler, showcasing the rich tapestry of mathematical development.

Takeaways

📚 The natural logarithm was discovered before the number e was defined, challenging our modern understanding of it as the logarithm with base e.
🔍 Initially, logarithms were not considered functions but as tables to simplify complex calculations, acting as primitive calculators.
📈 Logarithms transform multiplication into addition, division into subtraction, and finding nth roots into division by n, which was revolutionary in the pre-calculator era.
🌟 John Napier invented logarithms to address the complex calculations required in astronomy and navigation, starting with arithmetic and geometric progressions.
📊 Logarithms were first published by Napier in 1614 in 'Mirifici Logarithmorum Canonis Descriptio', sparking widespread interest and various translations.
🔢 The natural logarithm emerged from the work of William Oughtred and John Speidell, who created logarithm tables that closely resembled natural logarithms without knowing the number e.
📘 Logarithms were later connected to the area under the hyperbola, with Gregoire de Saint Vincent and Alfonso de Sarasa establishing a logarithmic relation between distance and area.
📐 Saint Vincent and Sarasa's work led to the first written form of a logarithm as a function, termed the 'hyperbolic logarithm'.
🤔 The term 'natural logarithm' was introduced by Nikolaus Mercator, though the reason for this naming is unclear.
🔄 The connection between logarithms and exponentials was fully recognized in the 18th century, leading to an understanding of the concept of a logarithm base.
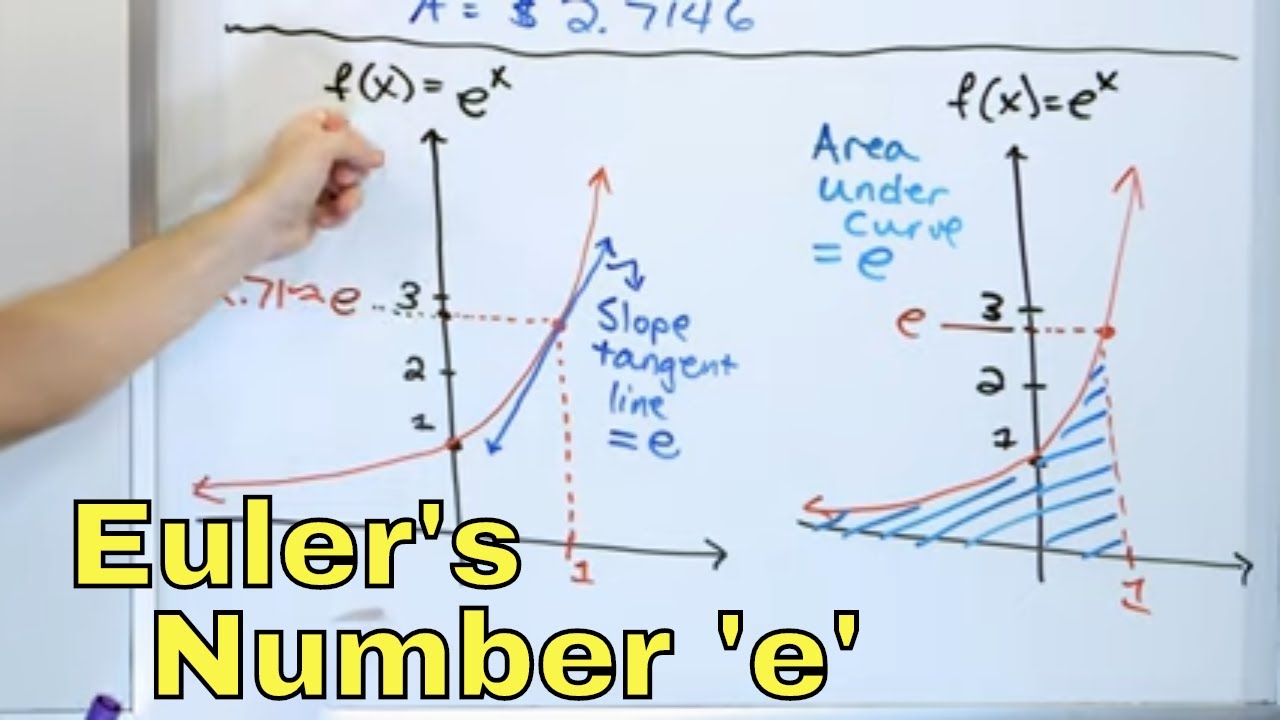
🧮 Euler calculated the base of the natural logarithm in 1748, identifying it as the number e, which is now universally recognized.

Q & A

What was the original purpose of logarithms before the connection with exponentials was recognized?
-The original purpose of logarithms was to serve as calculation tables that transformed multiplication into addition, division into subtraction, and finding the nth root into dividing by n, making complex calculations significantly faster and more manageable.
Why were logarithms considered invaluable during the pre-calculator age?
-Logarithms were invaluable because they simplified complex calculations related to astronomy and navigation, allowing for faster computation of tasks such as multiplication, division, and finding nth roots, which were otherwise very tedious.
Who is credited with the invention of logarithms and what was his initial approach?
-John Napier is credited with the invention of logarithms. His initial approach was to create tables that paired arithmetic and geometric progressions, which facilitated easier calculations.
How did the concept of logarithms evolve from being calculation tables to functions?
-The concept of logarithms evolved as mathematicians began to recognize the underlying mathematical relationships and patterns. Eventually, the connection between logarithms and exponentials was established, and logarithms were defined as inverse functions of exponentials.
What is the significance of the number e in the context of natural logarithms?
-The number e, also known as Euler's number, is the base of natural logarithms. It was discovered decades after the concept of natural logarithms was established and is fundamental to the definition of natural logarithms as logarithms with base e.
Why did Napier choose a number slightly less than 1 for his geometric progression in logarithm tables?
-Napier chose a number slightly less than 1 to fill in the gaps between entries in the logarithm tables, making the tables more practical for calculations. This approach allowed for a more continuous set of logarithmic values.
What was the role of William Oughtred in the development of logarithms?
-William Oughtred, one of Napier's students, is believed to have written an appendix in a translation of Napier's book that included a table of logarithms which closely resembled the natural logarithms of numbers, indicating an early connection to the concept of natural logarithms.
How did the concept of natural logarithms emerge in the study of the area under the hyperbola?
-Gregoire de Saint Vincent, building on Fermat's work, divided the area under the hyperbola into rectangles and found a pattern where the area could be expressed in terms of a logarithmic relation. This led to the recognition of natural logarithms as the area under the hyperbola.
What is the significance of the number 0.693147 in the context of natural logarithms?
-The number 0.693147 is the natural logarithm of 2. It is significant because it represents the value in the arithmetic progression that corresponds to the geometric progression value of 2 when using a base very close to 1, which is part of the process of deriving natural logarithms.
How did Leonhard Euler contribute to the understanding of natural logarithms?
-Leonhard Euler calculated the base of the natural logarithm and found it to be the number e. He also contributed to the understanding of logarithms by recognizing the connection between logarithms and exponentials, and by popularizing the use of the base e in mathematical expressions.

Outlines

00:00

📚 The Origins and Evolution of Logarithms

This paragraph introduces the concept of logarithms and their historical development. Initially, logarithms were not defined in terms of the base 'e' but were practical tools, essentially calculation tables that simplified complex arithmetic operations. The paragraph explains how multiplication was transformed into addition, division into subtraction, and finding nth roots into division by 'n'. It also discusses the invention of logarithms by John Napier in response to the computational challenges faced by astronomers and navigators during the 16th and 17th centuries. The explanation includes the pairing of arithmetic and geometric progressions to form logarithmic tables, which were revolutionary for their time.

05:04

🔍 The Natural Logarithm's Unexpected Discovery

This section delves into the discovery of the natural logarithm, which occurred before the number 'e' was even recognized. The paragraph discusses the limitations of Napier's logarithmic tables, particularly the gaps between entries, and how choosing a base close to 1 could fill these gaps. It describes Napier's process of creating logarithmic tables, including his use of a base slightly less than 1 and a shortcut involving sine tables. The paragraph also highlights the intriguing tables created by William Oughtred and John Speidell, which closely resemble natural logarithms, despite the lack of a recognized link between logarithms and exponentials at the time.

10:07

📉 The Hyperbolic Logarithm and the Area Under the Hyperbola

The focus shifts to the area under the hyperbola, a geometric challenge that stumped mathematicians for centuries. The paragraph explains Gregoire de Saint Vincent's method of dividing the area under the hyperbola into rectangles and how this led to the discovery of a logarithmic relationship between the distance along the hyperbola and the area. It describes Saint Vincent's insight that the distance progresses geometrically while the area progresses arithmetically, culminating in the hyperbolic logarithm, which was later calculated using an infinite series by Nikolaus Mercator and Isaac Newton.

15:08

🔑 The Natural Logarithm and the Number 'e'

The final paragraph wraps up the story of the natural logarithm, explaining how it evolved from the hyperbolic logarithm and was eventually connected to the base 'e'. It discusses the recognition of the connection between logarithms and exponentials, the understanding of the logarithm base, and Euler's identification of 'e' as the base of the natural logarithm. The paragraph concludes by reflecting on the full circle of the natural logarithm's history, from its origins as a practical tool to its formalization as a mathematical concept.

Mindmap

Keywords

💡Natural logarithm

The natural logarithm is the logarithm to the base e, where e is an irrational constant approximately equal to 2.71828. It is integral to the video's theme as it discusses the historical development and understanding of natural logarithms. The script mentions that the natural logarithm was discovered before the number e was defined, which is a key point in understanding the evolution of mathematical concepts.

💡Logarithm

A logarithm is the inverse operation to exponentiation, where the logarithm of a number is the power to which another fixed number, the base, must be raised to produce that number. In the video, the concept of logarithms is explored from their initial use as calculation tables to their modern definition as inverse functions of exponentials.

💡Exponential function

An exponential function is a mathematical function of the form f(x) = a * b^x, where a and b are constants, and b > 0, b ≠ 1. The script explains the relationship between exponential functions and logarithms, stating that logarithms are the inverse of these functions, which is a fundamental concept in modern mathematics.

💡Arithmetic progression

An arithmetic progression is a sequence of numbers in which each term after the first is obtained by adding a constant difference to the previous term. In the script, arithmetic progressions are used to create logarithmic tables, which were essential for simplifying complex calculations before the advent of calculators.

💡Geometric progression

A geometric progression is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio. The script describes how geometric progressions were paired with arithmetic progressions to create logarithmic tables for ease of calculation.

💡John Napier

John Napier was a Scottish mathematician who is renowned for his invention of logarithms. The script discusses Napier's contribution to simplifying complex calculations through the creation of logarithmic tables, which were revolutionary for the field of mathematics and related disciplines.

💡Calculation tables

Calculation tables are pre-computed values arranged in a way that simplifies complex mathematical operations. In the context of the video, logarithms were initially seen as calculation tables that transformed multiplication into addition and division into subtraction, which was a significant advancement for the time.

💡Hyperbola

A hyperbola is a type of conic section defined as the set of all points in a plane where the difference of the distances to two fixed points, the foci, is constant. The script discusses the historical challenge of calculating the area under the hyperbola, which eventually led to the discovery of the natural logarithm.

💡Gregoire de Saint Vincent

Gregoire de Saint Vincent was a Flemish mathematician who is credited with making significant contributions to the understanding of the area under the hyperbola. The script highlights Saint Vincent's work as a pivotal moment in the history of the natural logarithm, as he derived an equation for this area.

💡Euler's number (e)

Euler's number, commonly represented as 'e', is a fundamental mathematical constant that is the base of the natural logarithm. The script concludes with the story of how Euler calculated the base of the natural logarithm, identifying it as the number e, which is a crucial concept in understanding the natural logarithm.

💡Leonhard Euler

Leonhard Euler was a Swiss mathematician and physicist who made important contributions to a wide range of areas in mathematics including calculus and number theory. In the script, Euler is noted for calculating the base of the natural logarithm, which he identified as the number e, thus solidifying the connection between logarithms and exponentials.

Highlights

The natural logarithm was discovered decades before the number e, challenging our modern understanding of it being defined with base e.

Logarithms were initially invented as calculation tables to simplify complex multiplication, division, and root finding into addition, subtraction, and division by n.

John Napier invented logarithms as a solution to the tedious calculations required in astronomy and navigation.

Logarithms pair arithmetic and geometric progressions to transform multiplication into addition and division into subtraction.

Napier's logarithms filled gaps in calculation tables by choosing a base very close to 1, starting the geometric progression with 10 million.

Napier's logarithm tables were published in 1614 in 'Mirifici Logarithmorum Canonis Descriptio', sparking enthusiasm in the scientific community.

William Oughtred and John Speidell developed logarithm tables resembling natural logarithms independently, without knowing the link to exponentials or the number e.

Choosing a base slightly bigger than 1 for the geometric progression and a very small base for the arithmetic progression leads to natural logarithms.

Gregoire de Saint Vincent found an equation for the area under the hyperbola, which was the natural logarithm, by dividing the area into rectangles.

Saint Vincent's work showed a logarithmic relation between the distance and the area under the hyperbola, marking the first time a logarithm was written as a function.

Nikolaus Mercator and Isaac Newton provided an infinite series to calculate the hyperbolic logarithm, which Mercator named the natural logarithm.

The connection between logarithms and exponentials was finally recognized in the 18th century, leading to the understanding of the logarithm base concept.

Leonhard Euler calculated the base of the natural logarithm in 1748, identifying it as the number e, and the term 'natural logarithm' became widely accepted.

Logarithms evolved from being practical calculation tools to revealing deep mathematical relationships and contributing to the development of calculus.

Transcripts

Browse More Related Video

2.3 - Derivatives of Logarithmic Functions

14 - What is Euler's Number 'e', Ln(x) - Natural Log & e^x Functions?

Natural Logs and Differentiation

Logarithms - e - Euler's Number

The Derivative of ln(x) via Implicit Differentiation

Derivatives of Logarithmic Functions - More Examples