Contour plots | Multivariable calculus | Khan Academy

Khan Academy
5 May 201605:35
EducationalLearning
32 Likes 10 Comments

TLDRThe script explains the concept of a contour plot, a two-dimensional representation of a three-dimensional function. It describes how planes parallel to the x, y plane are used to create constant z-value slices, which are then projected onto the x, y plane as contour lines. These lines help visualize the function's output at different input points, with close spacing indicating steepness and concentric circles suggesting maxima or minima. The use of color to differentiate between output values further enhances the understanding of the function's behavior.

Takeaways
  • 📊 A three-dimensional graph represents a function with a two-dimensional input and a one-dimensional output, often visualized using graphing software.
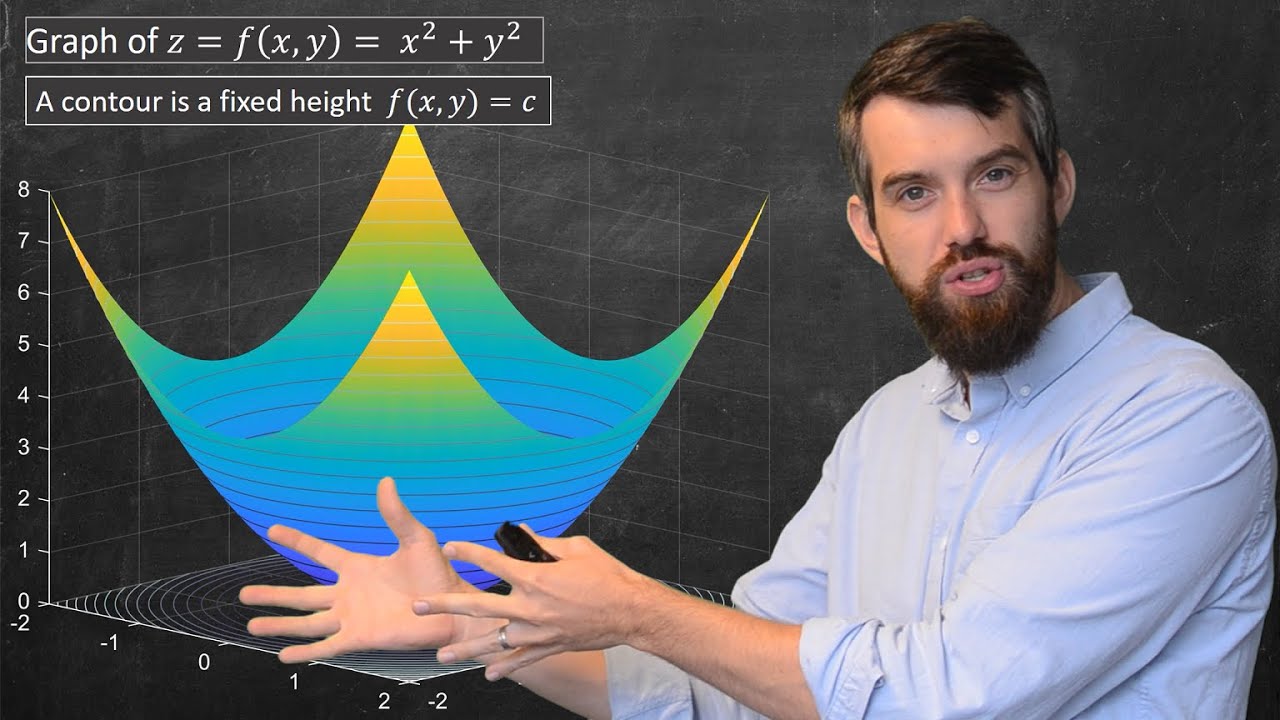
  • 🖋️ Contour plots offer a two-dimensional representation of three-dimensional functions by 'slicing' the graph at various z-values and drawing lines where these slices intersect the graph.
  • 🔪 The process involves 'squishing' the contour lines onto the x, y plane, creating a flat representation of the function's output values.
  • 📈 Contour lines represent constant output values of the function, similar to how lines on a two-dimensional graph represent constant values.
  • 📍 Each contour line corresponds to a specific output value of the function, which can be marked if necessary for clarity.
  • 📉 The spacing between contour lines indicates the steepness of the function; closely packed lines suggest a steep gradient, while widely spaced lines indicate a gentler slope.
  • 🔭 Contour plots can give a sense of the function's shape, allowing one to visualize how the graph might extend out of the page.
  • 🌀 Concentric circles in a contour plot often suggest a maximum or minimum point of the function.
  • 🎨 Coloring contour plots can enhance understanding by associating warmer colors with higher function values and cooler colors with lower values.
  • 🌈 The use of color in contour plots helps to visually distinguish between different output values and can provide a quick reference for the function's range.
  • 📝 Understanding contour plots is crucial for visualizing multi-dimensional functions on a two-dimensional surface, offering insights into the function's behavior across its input space.
Q & A

  • What is a three-dimensional graph representing?

    -A three-dimensional graph represents a function with a two-dimensional input and a one-dimensional output, typically visualized as f(x, y) = some expression involving x's and y's.

  • Why are traditional three-dimensional graphs considered clunky to draw?

    -Traditional three-dimensional graphs are clunky to draw because they usually require graphing software and cannot be easily scribbled down. Static images of them may not clearly convey the information.

  • What is a contour plot and how does it help in representing three-dimensional functions on a two-dimensional surface?

    -A contour plot is a method to represent three-dimensional functions on a two-dimensional surface by slicing the graph with planes parallel to the x, y plane and drawing lines where these planes intersect the graph, then projecting these lines onto the x, y plane.

  • What do the planes in a contour plot represent?

    -The planes in a contour plot represent constant values of z, with each plane corresponding to a different fixed value of z, allowing x and y to vary freely.

  • How are contour lines created in a contour plot?

    -Contour lines are created by identifying the points where the planes slicing the graph intersect with it, and then projecting these points onto the x, y plane.

  • What is the significance of the spacing between contour lines in a plot?

    -The spacing between contour lines indicates the steepness of the function. Closely spaced lines suggest a steep gradient, while widely spaced lines indicate a more gradual slope.

  • How can contour plots provide insight into the shape of a function?

    -Contour plots can provide insight into the shape of a function by showing the areas of constant output values and indicating the steepness or shallowness of the function's slope.

  • What is the purpose of coloring contour lines in a plot?

    -Coloring contour lines helps to visually distinguish between different levels of the function's output, with warmer colors typically representing higher values and cooler colors representing lower values.

  • Why might specific values be marked on contour lines in a plot?

    -Specific values are marked on contour lines to provide clarity on the exact output values that each line represents, which is especially important when precise information is needed.

  • How can the concept of concentric circles in contour plots be interpreted?

    -Concentric circles in contour plots often correspond to a maximum or minimum of the function, indicating areas where the function's output value is at its highest or lowest within the plotted region.

  • What is the main advantage of using contour plots over traditional three-dimensional graphs?

    -The main advantage of using contour plots is that they allow for a two-dimensional representation of multi-dimensional functions, making it easier to visualize and understand the function's behavior without the need for complex graphing tools.

Outlines
00:00
📈 Introduction to 3D Graphs and Contour Plots

This paragraph introduces the concept of three-dimensional graphs, which represent functions with two-dimensional inputs and a one-dimensional output, such as f(x, y). The speaker explains the limitations of traditional graphing methods, which can be cumbersome and static. To overcome these limitations, the concept of a contour plot is introduced as a way to represent these functions on a two-dimensional plane. The process involves slicing the graph with planes parallel to the x, y plane at various z values, creating contour lines that represent constant output values of the function. These contour lines are then projected onto the x, y plane, providing a simplified yet informative representation of the function's behavior.

05:02
🌈 Understanding Contour Plots with Color Coding

The second paragraph delves into the use of color coding in contour plots to enhance the visualization of multi-dimensional functions. Warmer colors like orange are used to represent higher values of the function, while cooler colors like blue indicate lower values. The contour lines act as boundaries between different colors, effectively communicating the range of output values across the input space. This method not only aids in understanding the function's behavior but also provides a visual representation of gradients, with closely spaced lines indicating steepness and widely spaced lines suggesting a more gradual slope. The use of color in contour plots is a powerful tool for quickly grasping the essence of complex functions.

Mindmap
Keywords
💡Three-dimensional graph
A three-dimensional graph is a visual representation of a function that takes two-dimensional inputs and produces a one-dimensional output. It is essential in the video's theme as it sets the stage for discussing how to represent complex functions in a more accessible way. The script uses the term to describe the initial representation of the function before introducing the concept of a contour plot.
💡Contour plot
A contour plot is a method of representing three-dimensional data in two dimensions by plotting constant z-values (or function outputs) as lines on an x-y plane. It is central to the video's message, illustrating a simplified way to visualize complex functions. The script describes how contour lines are derived from slicing the three-dimensional graph at various z-values and then projected onto the x-y plane.
💡Constant values
In the context of the video, constant values refer to the fixed z-values at which the three-dimensional graph is sliced to create the contour plot. These values are crucial for understanding the contour plot as they define the levels or lines that represent the function's output being constant. The script explains how different planes parallel to the x-y plane represent different constant z-values.
💡Function output
The function output is the result produced by a function given a set of inputs. In the video, the function output is visualized as the height above the x-y plane in a three-dimensional graph and is represented by the constant values on the contour plot. The script emphasizes the importance of understanding the function's output to interpret the contour plot correctly.
💡Slicing
Slicing, in the script, refers to the process of cutting the three-dimensional graph at various z-values to create the contour lines. It is a key action in transforming the 3D representation into a 2D contour plot. The script uses this term to describe how different planes are used to capture the essence of the function at different heights.
💡Contour lines
Contour lines are the lines on a contour plot that connect points of equal function output. They are a fundamental concept in the video, as they represent the intersection of the slices with the three-dimensional graph. The script explains that these lines are then projected onto the x-y plane to create the two-dimensional representation.
💡X-Y plane
The x-y plane is the horizontal plane in a three-dimensional space where the graph's input variables, x and y, are plotted. In the video, the x-y plane is significant as it is the surface onto which the contour lines are eventually projected to create the contour plot. The script mentions it in the context of slicing the graph and projecting the contour lines.
💡Steepness
Steepness in the video refers to the rate of change of the function's output with respect to its inputs. It is illustrated by the spacing of the contour lines; closely spaced lines indicate a steep gradient, while widely spaced lines suggest a more gradual slope. The script uses steepness to help viewers understand the function's behavior in different regions of the input space.
💡Concentric circles
Concentric circles on a contour plot represent a series of constant output levels that are equidistant from a central point, often indicating a maximum or minimum of the function. The video mentions these as a common feature in contour plots, helping to visualize the function's extremities. The script describes how these circles can provide insight into the shape of the function.
💡Coloring
In the context of contour plots, coloring refers to the use of different hues to represent varying levels of the function's output. The video discusses this as a way to enhance the visualization, with warmer colors for higher values and cooler colors for lower values. The script explains that this technique can help in quickly identifying the range of outputs across the input space.
Highlights

Three-dimensional graphs represent functions with a two-dimensional input and a one-dimensional output.

Contour plots are used to represent these functions two-dimensionally.

Contour plots are created by slicing the graph with planes parallel to the x, y plane.

Each slice represents a constant value of the function's output.

Contour lines are drawn where the slices cut into the graph.

These contour lines are then flattened onto the x, y plane.

Flattened contour plots provide a two-dimensional representation of the function's outputs.

Contour plots help visualize functions with a two-dimensional input and one-dimensional output.

Each contour line corresponds to a constant output value of the function.

The spacing of contour lines indicates the steepness of the function.

Closely spaced contour lines represent steep regions of the function.

Widely spaced contour lines represent shallow regions of the function.

Concentric circles in contour plots often indicate a maximum or minimum value.

Color-coding can be used to represent different output values in contour plots.

Contour plots with color provide a more intuitive understanding of multi-dimensional functions.

Transcripts

Browse More Related Video

Introduction to 3d graphs | Multivariable calculus | Khan Academy

Visualizing Multi-variable Functions with Contour Plots

Three-Dimensional Coordinates and the Right-Hand Rule

Parametric curves | Multivariable calculus | Khan Academy

Functions of Several Variables!

Basic Euclidean Geometry: Points, Lines, and Planes

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Contour PlotsData Visualization3D GraphsFunction AnalysisZ-PlanesX-Y PlaneConstant ValuesGraph InterpretationSteepness IndicatorColor CodingEducational Tool