Calculus 3: Lecture 11.5 Lines and Planes in Space

The Math Sorcerer

4 Feb 2020116:39

EducationalLearning

32 Likes 10 Comments

TLDRThis script is a detailed mathematical lecture on deriving the equations of lines and planes in three-dimensional space. It covers the concepts of parametric and symmetric equations for lines, and the general form equation for planes. The instructor uses a step-by-step approach, starting from basic principles and gradually building up to more complex problem-solving. The lecture includes examples and homework problems to illustrate the application of these mathematical concepts, emphasizing the importance of understanding the derivations and the logic behind each step.

Takeaways

📚 The script is a detailed lecture on deriving the equations of lines and planes in three-dimensional space from scratch.
📏 It explains that for a line in 3D, given a point and a parallel vector, the equation of the line can be determined using parametric equations.
🧭 The concept of direction vectors and direction numbers is introduced, highlighting their role in defining the orientation of a line in space.
🤔 The lecture emphasizes the importance of understanding derivations and the logic behind the equations, rather than just memorizing them.
📈 The process of deriving the equation of a line involves setting up vectors and using the concept that the difference between any two points on the line is a multiple of the direction vector.
📉 For planes, the script describes how a point on the plane and a perpendicular (normal) vector can be used to derive the equation of the plane.
📐 The cross-product is introduced as a method to find a normal vector to the plane when given two points on the plane, which can then be used to find the plane's equation.
🔍 The lecture includes examples and exercises to illustrate the process of finding parametric and symmetric equations for lines and planes.
📝 The importance of correctly interpreting mathematical notation and understanding the mathematical concepts behind it is stressed throughout the lecture.
🔢 The script also touches on the application of these concepts in real-world scenarios, such as modeling paths in space for navigation or flight.
💡 Lastly, the lecture encourages students to engage with the material actively, suggesting that they try solving problems on their own before checking with the provided solutions.

Q & A

What is the main topic discussed in the script?
-The main topic discussed in the script is the derivation and understanding of the equations for lines and planes in three-dimensional space.
What is the significance of a direction vector in the context of lines in 3D space?
-A direction vector in the context of lines in 3D space is crucial as it defines the direction of the line. It is used to express any point on the line as a multiple of the direction vector plus a fixed point on the line.
What are parametric equations, and how do they relate to lines in 3D space?
-Parametric equations are a way to describe the path of a point in space as a function of a parameter, typically denoted as 'T'. In the context of lines in 3D space, parametric equations express the coordinates of any point on the line in terms of the direction vector and a parameter that varies along the line.
What is the role of the normal vector in defining a plane in 3D space?
-The normal vector to a plane in 3D space is perpendicular to the plane. It is used in the equation of the plane to ensure that any vector lying on the plane is orthogonal to the normal vector, which helps in defining the plane's orientation in space.
Why is the dot product of a normal vector and a vector on the plane equal to zero?
-The dot product of a normal vector and a vector on the plane is equal to zero because the normal vector is perpendicular to every vector on the plane. The dot product of two perpendicular vectors is always zero.
What is the general form of the equation of a plane in 3D space?
-The general form of the equation of a plane in 3D space is given by aX + bY + cZ = d, where (a, b, c) represents the components of the normal vector to the plane, and 'd' is a constant that represents the plane's distance from the origin along the normal vector.
How can you find the equation of a plane given two points on the plane?
-To find the equation of a plane given two points, you first find a vector that is parallel to the plane by subtracting the coordinates of the two points. Then, you can find a normal vector to the plane by taking the cross product of two such parallel vectors. Finally, you use the normal vector and a point on the plane to write the plane's equation.
What is the significance of the parameter 'T' in parametric equations of a line?
-In parametric equations of a line, the parameter 'T' represents a scalar multiplier that, as it varies, allows you to find every point on the line. It can be thought of as a measure of 'time' or 'position' along the line, with different values of 'T' corresponding to different points.
How can you find the symmetric equations of a line from its parametric equations?
-To find the symmetric equations of a line from its parametric equations, you solve each of the parametric equations for 'T'. This gives you an expression that relates the difference in coordinates of any point on the line to the parameter 'T', which is the symmetric form.
What is the difference between a direction vector and a normal vector in the context of lines and planes?
-A direction vector for a line in 3D space is parallel to the line and indicates its direction. In contrast, a normal vector for a plane is perpendicular to the plane and defines its orientation in space. The direction vector helps define the position of points on the line, while the normal vector is used in the plane's equation to ensure that all points on the plane satisfy the equation.

Outlines

00:00

📚 Derivation of a 3D Line Equation

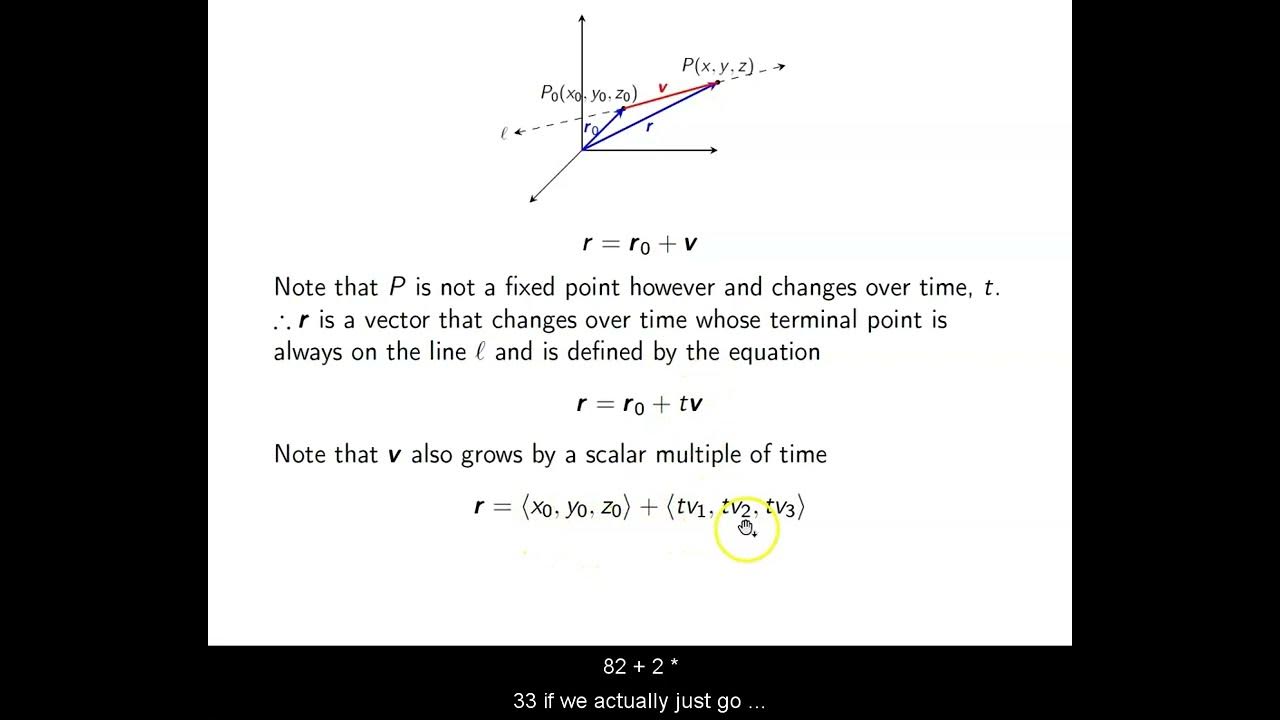
The paragraph introduces the mathematical concept of deriving the equation of a line in three-dimensional space. It explains that given a point on the line and a parallel vector, one can determine the line's path. The instructor begins by setting up the axes and identifying a point P on the line with coordinates (x1, y1, z1). A direction vector V, represented by its direction numbers (A, B, C), is also introduced. The parallel relationship between the line and the vector is emphasized, leading to the derivation of the line's equation using a parameter T, which represents a scalar multiple in the direction vector.

05:01

🔍 Parametric Equations of a 3D Line

This section delves into the derivation of parametric equations for a line in 3D space. The instructor uses the point P and the direction vector V to establish the parametric equations, which are expressed as x = x1 + At, y = y1 + Bt, and z = z1 + Ct. The parameter T is highlighted as a way to describe the position on the line as it varies, akin to time in many real-world applications. The symmetric equations are also introduced, allowing one to solve for T given a point on the line, and the importance of the direction numbers (A, B, C) being non-zero is discussed.

10:03

📘 Solving for Parametric and Symmetric Equations

The instructor provides a step-by-step guide on how to solve for the parametric and symmetric equations of a line given specific points and direction vectors. The process involves plugging in values into the formulas derived earlier and simplifying the expressions to find the equations that describe the line. The paragraph includes an example with given points and direction numbers, leading to the calculation of the parametric equations and symmetric equations, which are essential for various applications in mathematics.

15:07

🎯 Applying Parametric Equations in Practice

The paragraph discusses the practical application of parametric equations in various mathematical and real-world scenarios. It emphasizes the importance of understanding the derivation process and being able to explain it to others. The instructor provides an example of how the parametric equations can be used to describe the position on a line as a function of time, T. The concept is illustrated by showing how different values of T correspond to different points on the line, effectively modeling motion along the line.

20:11

📐 Deriving the Equation of a Plane

This section focuses on deriving the equation of a plane in three-dimensional space. The instructor explains that a point on the plane and a perpendicular vector are needed to define the plane. The process involves using the dot product of the perpendicular vector (A, B, C) and the vector formed by any point on the plane (X, Y, Z) minus the given point (x1, y1, z1), which results in the equation A(X - x1) + B(Y - y1) + C(Z - z1) = 0. The importance of the normal vector and its components is highlighted in this derivation.

25:11

🛠 Finding the Normal Vector to a Plane

The paragraph discusses the process of finding the normal vector to a plane, which is crucial for determining the plane's equation. It explains that the normal vector is perpendicular to the plane and can be found using the cross-product of two vectors that lie on the plane. The instructor provides an example with given points on the plane and guides through the calculation of the normal vector, which is then used in the plane's equation.

30:11

📉 Solving Plane Equations with Given Points and Perpendicular Vectors

The instructor provides a detailed explanation of how to solve for the equation of a plane when given two points on the plane and a perpendicular vector. The process involves finding a direction vector from the given points and then using the cross-product to find the normal vector. The normal vector components are then used in the general form of the plane equation to find the solution. The paragraph includes an example that walks through the entire process.

35:12

📝 Working Through Plane Equation Problems

This paragraph describes the process of working through various plane equation problems, emphasizing the importance of understanding the underlying concepts rather than just memorizing formulas. The instructor discusses different types of problems, including those where the plane is perpendicular to a given vector or contains a given line. The paragraph highlights the need to carefully read and understand the problem statement before applying the appropriate mathematical techniques.

40:13

🎓 Comprehensive Review of Plane Equations

The paragraph serves as a comprehensive review of the concepts covered regarding plane equations. It includes a discussion on the general form of the equation, the significance of the normal vector, and the process of finding the equation of a plane given different sets of information. The instructor emphasizes the importance of practice and understanding the derivation process for each type of problem.

Mindmap

Keywords

💡Parametric Equations

Parametric equations are a mathematical method used to describe the path of a point in space as a function of a parameter, often denoted as 'T'. In the context of the video, these equations are used to represent lines in 3D space. The script explains that for each value of T, there is a corresponding point on the line, allowing for the modeling of the line's path over time. For instance, the video mentions 'x equals x1 plus ta' as part of the parametric equations for a line.

💡Symmetric Equations

Symmetric equations are a form of representation for lines and planes that relate the differences in coordinates to a constant. The script discusses symmetric equations in the context of lines, stating that 'X minus x1 over a equals y minus y1 over B, equals Z minus Z1 over C'. These equations are derived from the parametric form and provide an alternative way to express the relationship between points on a line.

💡Direction Vector

A direction vector is a vector that indicates the direction of a line or plane in space. In the video, the direction vector is denoted as 'V' and is described as being parallel to a line 'L'. The script emphasizes that the direction vector contains the direction numbers 'a', 'b', and 'c', which are essential for deriving the parametric and symmetric equations of a line.

💡Normal Vector

A normal vector is perpendicular to a plane. The script introduces the concept of a normal vector when discussing the equation of a plane, stating that a plane can be defined by a point on the plane and a perpendicular vector. The normal vector is crucial for deriving the equation of a plane and is represented by the components 'A', 'B', and 'C' in the script.

💡Cross-Product

The cross-product is a mathematical operation that takes two vectors and returns a vector perpendicular to the plane containing the two original vectors. In the script, the cross-product is used to find a normal vector to a plane when two vectors lying on the plane are known. For example, the script describes finding the cross-product of vectors 'u' and 'v' to obtain the normal vector 'n'.

💡Dot Product

The dot product is an operation that takes two vectors and returns a scalar. It is used to determine the angle between two vectors and whether they are perpendicular. In the context of planes, the script mentions that the dot product of a normal vector and any vector on the plane is zero, indicating orthogonality.

💡Perpendicular

Perpendicular lines or vectors meet at a right angle. The script frequently refers to perpendicularity, especially when discussing the relationship between planes and lines or between a line and a direction vector. For instance, the script states that a plane is perpendicular to a line if the direction vector of the line is perpendicular to the plane.

💡Parallel

Parallel lines or vectors never meet and are equidistant from each other. The script discusses the concept of parallelism in the context of direction vectors being parallel to a line and the relationship between a plane and a vector being parallel if they do not intersect. The script uses the term to explain how to derive equations of lines and planes.

💡Vector

A vector is a mathematical object that has both magnitude and direction. In the script, vectors are used extensively to describe lines and planes in three-dimensional space. For example, the script mentions 'vector PQ' as the vector formed between two points on a line, and 'vector V' as a direction vector parallel to a line.

💡Plane

A plane is a flat, two-dimensional surface that extends infinitely in all directions. The script discusses planes in the context of finding their equations given points on the plane and perpendicular or parallel vectors. The script also explains how to derive the equation of a plane from a point and a normal vector, using the formula 'a(x - x1) + b(y - y1) + c(z - z1) = 0'.

Highlights

Introduction to deriving the equation of a line in 3D space from a point and a parallel vector.

Explanation of the concept of direction vectors and direction numbers in the context of lines in 3D.

Derivation of parametric equations for a line in 3D space using a point and a direction vector.

Illustration of how to find a line by distributing the parameter T across the components of the direction vector.

The significance of the parameter T in parametric equations, representing a point on the line as T varies.

Introduction to symmetric equations as an alternative representation of a line in 3D space.

Derivation of symmetric equations from parametric equations by solving for the parameter T.

Explanation of how the direction vector's components cannot be zero when deriving symmetric equations.

Demonstration of how to manipulate the direction vector by multiplying it by a scalar to simplify calculations.

Transition to the derivation of the equation of a plane in 3D space from a point and a normal vector.

Description of the normal vector's role in defining the orientation of a plane perpendicular to it.

Derivation of the general form equation for a plane using the dot product of the normal vector and a vector on the plane.

Clarification on the importance of correctly identifying the normal vector to the plane for accurate equation formulation.

Discussion on the different forms of plane equations and how they can be derived from one another.

Practical application of plane equations in various mathematical and real-world scenarios.

Overview of the process for finding the equation of a plane given three points in 3D space.

Use of the cross-product to find a normal vector from two vectors lying on the plane.

Final remarks on the importance of understanding the conceptual framework behind deriving equations of lines and planes in 3D space.

Transcripts

Browse More Related Video

Ch. 9.6 Equations of Lines and Planes

Calculus AB Homework 4.1: Implicit Differentiation

Calculus 3: Equations of Lines and Planes (Video #5) | Math with Professor V

Lec 5: Parametric equations for lines and curves | MIT 18.02 Multivariable Calculus, Fall 2007

Basic Euclidean Geometry: Points, Lines, and Planes

DIMENSIONAL ANALYSIS FOR BEGINNERS

Related Tags

3D Geometry Equation Derivation Vector Analysis Parametric Lines Symmetric Equations Plane Theory Cross-Product Perpendicular Vectors Mathematics Education Conceptual Understanding