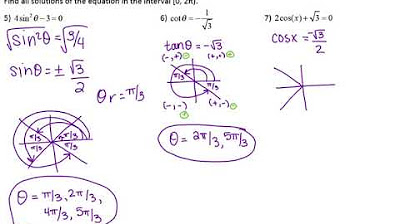Solving Math Equations but they keep getting HARDER | jensenmath.ca

JensenMath

15 Feb 202423:28

EducationalLearning

32 Likes 10 Comments

TLDRThis script presents a math challenge, guiding viewers through 11 progressively difficult equations, starting with simple linear equations and culminating in complex exponential and trigonometric problems. The solution process involves various algebraic techniques, such as factoring, using logarithms, and applying trigonometric identities. The video aims to test and enhance the viewer's problem-solving skills, encouraging them to engage with the material and share their progress.

Takeaways

📚 The video presents a series of 11 progressively difficult math equations to solve, starting with simple linear equations and ending with a complex exponential equation.
🔍 The first equation is a basic linear equation solved by isolating x using inverse operations, resulting in x = 6.
📉 For the second equation, multiplying both sides by three eliminates the fraction and leads to x = 3 after simplifying.
🔢 The third equation is a quadratic equation solved by factoring, yielding two solutions, x = -6 and x = 2.
📈 The fourth equation involves factoring a quadratic expression after taking out a common factor, resulting in solutions y = 1 and y = 3/5.
🌐 The fifth equation is an exponential equation where rewriting the bases as powers of the same number allows solving for x = -6.
✅ The sixth equation involves logarithms, where taking the common logarithm of both sides and applying logarithmic identities leads to an approximate solution of x ≈ 1.86.
📐 The seventh equation is a trigonometric equation solved by finding angles with a sine ratio of -1/2, resulting in two solutions within the range of 0 to 2π.
🔑 The eighth equation is a polynomial equation solved by factoring and synthetic division, leading to solutions x = -1, 2, 3, and -3.
🔍 The ninth equation is a logarithmic equation where combining logarithms and applying the quadratic formula results in a solution of x = 2 + √14, with the negative solution being extraneous.
📉 The tenth equation involves trigonometric identities and results in two sets of solutions for x based on the tangent function, with an infinite number of co-terminal angles possible.
💡 The eleventh and most difficult equation is an exponential equation that, when manipulated, reveals a hidden quadratic equation, solved using factoring and logarithms, with solutions for x being logarithmic and approximate.

Q & A

What is the main objective of the video?
-The main objective of the video is to solve 11 progressively difficult mathematical equations, explaining the process for each one.
How does the video approach the first equation?
-The video approaches the first equation by using inverse operations to isolate the variable x, starting with adding 7 to both sides and then dividing by 3 to find the value of x.
What strategy is used for the second equation to eliminate the fraction?
-The strategy used for the second equation is to multiply both sides by 3 to eliminate the fraction and then isolate the variable x by combining like terms and dividing by 2.
How does the video solve the third quadratic equation?
-The video solves the third quadratic equation by factoring, finding two numbers that multiply to -12 and add up to 4, which are 6 and -2, and then using the zero product rule to find the solutions x = -6 and x = 2.
What method is used in the fourth equation to factor the quadratic expression?
-The method used in the fourth equation is to take out a common factor of 2, then use the long division method to factor by grouping, and finally apply the zero product rule to find the solutions y = 1 and y = 3/5.
How does the video handle the fifth exponential equation?
-The video handles the fifth exponential equation by rewriting the base of the power on the right to match the base on the left, then equating the exponents and solving for x = -6.
What logarithmic approach is taken in the sixth equation?
-In the sixth equation, the video takes the common logarithm of both sides to remove the exponent and then uses the properties of logarithms to isolate x, resulting in an approximate solution of x ≈ 1.86.
How are the solutions to the seventh trigonometric equation determined?
-The solutions to the seventh trigonometric equation are determined by isolating sinx and using the properties of the sine function in different quadrants, resulting in two solutions x = 7π/6 and x = 11π/6, with the possibility of infinite co-terminal angles.
What is the initial step for solving the eighth polynomial equation?
-The initial step for solving the eighth polynomial equation is to test for possible zeros by evaluating the function at factors of the constant term, finding that x = -1 is a zero and then using synthetic division to factor the polynomial.
How does the video solve the ninth logarithmic equation?
-The video solves the ninth logarithmic equation by combining the logarithms and rewriting the equation in exponential form, then applying the quadratic formula to find the solutions, considering the domain restrictions of logarithmic functions.
What identity is used in the tenth equation to simplify the trigonometric expression?
-The identity used in the tenth equation is secant squared x equals tangent squared x plus one, which is then simplified to a quadratic form in terms of tangent x.
How is the final eleventh equation approached to reveal the hidden quadratic?
-The final eleventh equation is approached by multiplying both sides by 2 to the power of x to reveal a hidden quadratic, which is then solved by factoring and using logarithms to find the exponents.

Outlines

00:00

📚 Introduction to Solving 11 Equations

The video script introduces a series of 11 mathematical equations that increase in difficulty. The purpose is to find the value of 'x' that balances each equation. The speaker begins with a simple linear equation, demonstrating the process of isolating 'x' by inverse operations. The solution to the first equation is x = 6, achieved by adding 7 to both sides and then dividing by 3.

05:01

🔍 Simplifying Linear and Quadratic Equations

The script continues with a linear equation involving fractions, which is simplified by multiplying both sides by 3 to eliminate the fraction. The solution is x = 3, found by isolating the variable and dividing by 2. The third equation is a quadratic equation solved by factoring, yielding two solutions, x = -6 and x = 2. The fourth equation is another quadratic, this time factored by grouping, resulting in solutions y = 1 and y = 3/5.

10:04

🔢 Solving Exponential and Logarithmic Equations

The fifth equation is an exponential equation where the bases are made the same, and the exponents are set equal to solve for x = -6. The sixth equation involves taking the common logarithm to remove the exponent and isolate the variable, resulting in an approximate solution of x ≈ 1.86. The seventh equation is a trigonometric equation, solved by considering the sign of the sine function and finding two solutions within the range of 0 to 2π.

15:05

📐 Trigonometric and Polynomial Equations

The eighth equation is a polynomial equation solved by finding factors through synthetic division, leading to solutions x = -1, 2, 3, and -3. The ninth equation is a logarithmic equation where the argument of the logarithm must be positive, resulting in a valid solution of x = 2 + √14 after discarding the extraneous root.

20:06

🧭 Advanced Trigonometric and Exponential Equations

The tenth equation involves two different trigonometric functions and is simplified using an identity to form a quadratic equation in terms of 'k', where 'k' represents tan(x). The solutions for 'k' are then translated into solutions for 'x', considering the periodic nature of the tangent function. The eleventh and final equation is an advanced exponential equation that, after manipulation, reveals a hidden quadratic form, leading to solutions for 2^x being 3 and 4, with the latter solved exactly and the former approximated using a logarithm.

Mindmap

Keywords

💡Equation

An equation is a mathematical statement that asserts the equality of two expressions. In the video, equations serve as the central theme, with the host solving a series of increasingly complex equations to demonstrate various mathematical techniques. The first equation, for example, is a simple linear equation that is solved by isolating the variable x, illustrating the basic concept of an equation.

💡Inverse Operations

Inverse operations are mathematical processes that 'undo' a previous operation. In the context of the video, the host uses inverse operations to solve equations, such as adding seven to cancel out a subtraction of seven, demonstrating how to isolate variables in linear equations.

💡Quadratic Equation

A quadratic equation is a polynomial equation of degree two, typically in the form of ax^2 + bx + c = 0. The video explains how to solve quadratic equations by factoring or using the quadratic formula. The third equation in the script is a quadratic equation solved by factoring, showcasing the process of finding two possible solutions.

💡Exponential Equation

An exponential equation involves a variable in the exponent. The video discusses solving such equations by rewriting bases or using logarithms. For instance, the fifth equation involves rewriting the base of a power to have the same base as another power, then equating the exponents to solve for x.

💡Logarithm

A logarithm is the inverse operation to exponentiation, used to solve equations where the variable is an exponent. The video script describes using logarithms to isolate the variable, as seen in the sixth equation where the common logarithm is applied to both sides of the equation to simplify it.

💡Trigonometric Functions

Trigonometric functions, such as sine and tangent, relate angles of a triangle to the lengths of its sides. The video includes solving trigonometric equations, where the host finds the angles that satisfy the given conditions. The seventh equation involves finding the angles for which the sine function equals 1/2, using knowledge of special triangles.

💡Factoring

Factoring is the process of breaking down a polynomial into a product of its factors. The video demonstrates factoring in the context of solving polynomial equations, like the eighth equation, where the polynomial is factored to find its roots.

💡Synthetic Division

Synthetic division is a simplified method of polynomial division used when the divisor is a linear factor. In the script, synthetic division is used to divide the polynomial by x + 1, providing a more efficient way to factor the polynomial and find its zeros.

💡Quadratic Formula

The quadratic formula is a method for solving quadratic equations when they cannot be factored easily. It is given by x = (-b ± √(b^2 - 4ac)) / (2a). The video script applies the quadratic formula to the ninth equation, where the quadratic does not factor nicely, to find the values of x.

💡Extraneous Root

An extraneous root is a solution that arises from the algebraic manipulation process but does not satisfy the original equation. In the video, the host identifies an extraneous root in the context of solving a logarithmic equation, where a potential solution makes the argument of a logarithm negative, thus invalidating it.

💡Secant and Tangent

Secant and tangent are trigonometric functions that relate to the geometry of circles and triangles. The video discusses an equation involving both secant and tangent, using the identity secant squared x equals tangent squared x + 1 to transform the equation into a solvable quadratic form.

💡Difference of Squares

The difference of squares is a factoring technique used for expressions of the form a^2 - b^2, which can be factored into (a + b)(a - b). In the script, the host applies this technique to the factored form of a polynomial to further break it down into simpler factors, aiding in finding the roots of the equation.

💡Power of a Power Rule

The power of a power rule states that when raising a power to another power, you multiply the exponents. The video uses this rule in the final equation to transform an exponential equation into a quadratic form by rewriting 2^(2x) as 2^x squared, revealing a hidden quadratic equation.

Highlights

Introduction to solving a series of 11 progressively difficult equations.

Solving the first simple linear equation by isolating x using inverse operations.

Explanation of the process to eliminate fractions in linear equations by multiplying both sides.

Isolating x in a linear equation by combining like terms and dividing by the coefficient.

Approach to solving quadratic equations by setting them to zero and factoring.

Using the zero product rule to find two solutions for a quadratic equation.

Factoring a quadratic equation by taking out a common factor and using the zero product rule.

Solving an exponential equation by rewriting bases and equating exponents.

Using logarithms to solve an exponential equation with different bases.

Isolating x in an exponential equation by applying logarithmic properties.

Finding solutions to a trigonometric equation within a specific range using special triangles.

Identifying an infinite number of solutions for a trigonometric equation and their relationship.

Solving a polynomial equation by testing for zeros and using synthetic division.

Factoring a polynomial completely to find all possible solutions.

Solving a logarithmic equation by converting it to exponential form and applying the quadratic formula.

Determining the valid solution for a logarithmic equation by considering the domain restrictions.

Using trigonometric identities to simplify and solve a complex trigonometric equation.

Finding multiple solutions for a trigonometric equation by considering the periodicity of the tangent function.

The final and most difficult exponential equation with a hidden quadratic form.

Solving the hidden quadratic in an exponential equation by factoring and using logarithms.

Conclusion of the 11 high school math level equations with a call to action for feedback.

Transcripts

Browse More Related Video

Paper 1 common exam questions

Precalc Chapter 5 Review

Verifying Trigonometric Identities Easily - Strategy Explained (14 Examples)

5.5 Multiple Angle and Product to Sum Formulas (Part 1)

Intro to Trigonometric Identities - part 1

DERIVATIVES that keep getting HARDER 🤯 | jensenmath.ca

Related Tags

Math Equations Educational Walkthrough Linear Equations Quadratic Exponential Trigonometry Logarithmic Algebra Problem Solving High School Math