Verifying Trigonometric Identities Easily - Strategy Explained (14 Examples)

Mario's Math Tutoring

3 Feb 202025:08

EducationalLearning

32 Likes 10 Comments

TLDRThe video script is an engaging walkthrough of 14 challenging trigonometric identity problems aimed at enhancing the viewer's understanding and proficiency in trigonometry. The presenter encourages viewers to attempt each problem and share their solutions in the comments section. The script emphasizes a methodical approach to solving these problems, often starting with the more complex side and simplifying it to match the simpler side. It leverages the use of Pythagorean trig identities and the properties of trigonometric functions to guide the viewer through each step. The presenter also shares helpful tips, such as multiplying by the conjugate and factoring out common terms, to simplify the process. The script concludes with a prompt for viewers to engage with the content by commenting on their success rate with the problems, fostering a sense of community and learning.

Takeaways

📚 Start by identifying the more expanded or complicated side of the trigonometric identity and work towards simplifying it to match the more condensed side.
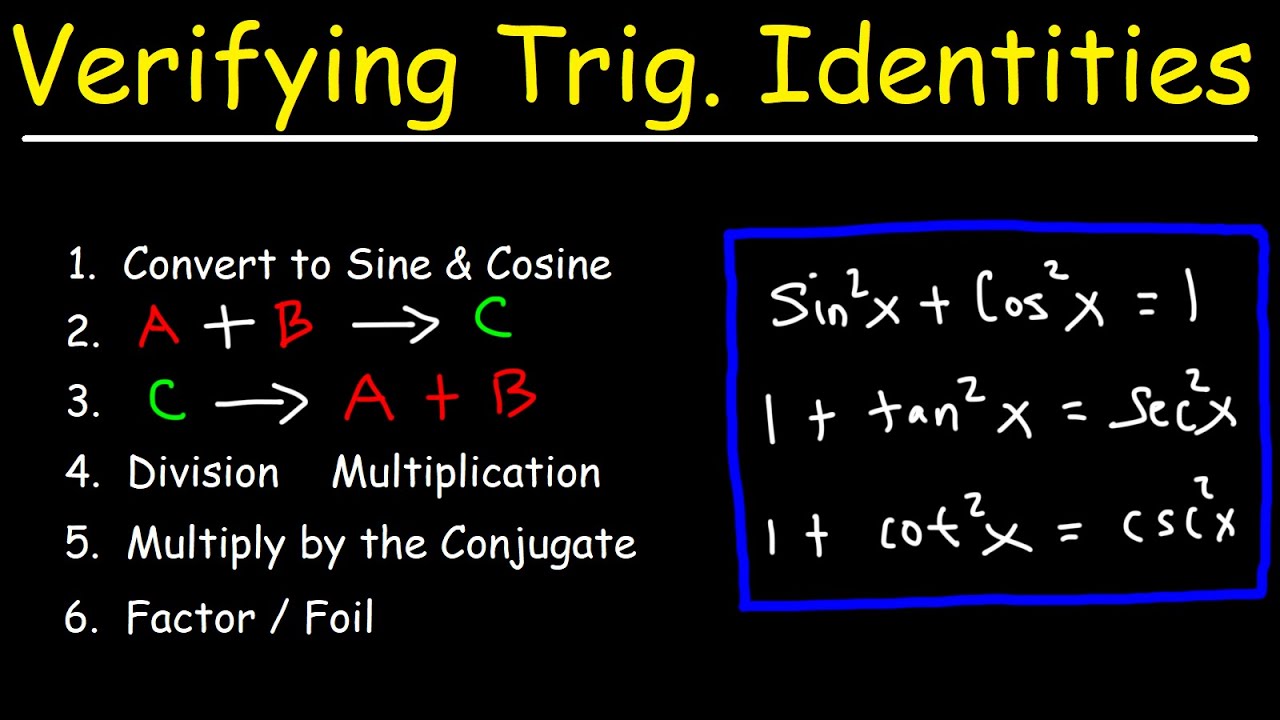
🧩 Use Pythagorean trig identities frequently, as they are helpful in simplifying and proving trigonometric identities.
✅ Replace cosecant squared minus 1 with cotangent squared to simplify expressions, leveraging the relationship between these functions.
🔄 Multiply by the conjugate when dealing with binomial expressions to help simplify and find a common denominator.
🤔 When stuck, convert back to sines and cosines, which are the basic building blocks of trigonometric functions.
📉 Factor out the greatest common factor in complex expressions to simplify the process of proving identities.
🔢 Memorize or have Pythagorean trig identities on hand, as they are often used in the process of identity verification.
🤓 Practice is key to getting better at verifying trigonometric identities, as recognizing patterns and substitutions improves with experience.
📝 Keep an eye on both sides of the identity while working, ensuring that you are moving towards the desired simplified form.
📉 Use the even and odd identities for negative angles, which can simplify expressions involving negative theta values.
📌 Always check your work by distributing back into the original expression after factoring to ensure accuracy.

Q & A

What is the general strategy for verifying trigonometric identities as described in the video?
-The general strategy for verifying trigonometric identities involves focusing on the more complex side of the identity and simplifying it to match the simpler side. This often includes using Pythagorean trigonometric identities and making substitutions to simplify the expression.
What are Pythagorean trigonometric identities and why are they frequently used in the video?
-Pythagorean trigonometric identities are equations that relate the squares of the basic trigonometric functions (sine, cosine, and tangent) to each other. These identities are frequently used because they simplify the manipulation of trigonometric expressions, especially when verifying identities.
What technique is suggested for handling trigonometric expressions involving squared terms?
-When dealing with trigonometric expressions involving squared terms, the video suggests using Pythagorean trigonometric identities to simplify these terms, often by substituting one function for another based on these identities.
How does the video explain the process of combining fractions in trigonometric identities?
-The video explains that combining fractions in trigonometric identities typically involves finding a common denominator for the fractions involved, then combining the numerators accordingly to simplify the expression to match the other side of the identity.
What is the significance of the cofunction identities mentioned in the video?
-Cofunction identities are used to relate trigonometric functions of complementary angles, such as sine and cosine, or tangent and cotangent. These identities are significant because they allow substitutions that can simplify the verification of identities involving angles like π/2 - θ.
Can you describe a scenario from the video where a trigonometric function of a negative angle is used, and how it's handled?
-In the video, trigonometric functions of negative angles are handled using even and odd identities. For example, sine is an odd function and cosine is an even function, which means the sine of a negative angle is the negative sine of the angle, and the cosine of a negative angle is the cosine of the angle. This property is used to simplify expressions involving negative angles.
What role do reciprocal identities play in verifying trigonometric identities as per the video?
-Reciprocal identities relate trigonometric functions to their reciprocals, such as sine and cosecant, or cosine and secant. These identities are crucial for simplifying expressions by allowing the substitution of one function for its reciprocal, thereby reducing the complexity of the identity being verified.
Why does the video emphasize practicing with different trigonometric identities?
-The video emphasizes practicing with different trigonometric identities to build familiarity and skill in manipulating these functions. This practice helps learners recognize patterns and develop strategies for simplifying and verifying identities more efficiently.
How is factoring used as a technique in verifying trigonometric identities in the video?
-Factoring is used as a technique to pull out common factors from terms in an expression, simplifying the rest of the expression. This is particularly useful in cases where the identity involves complex expressions that can be broken down into simpler, common components.
What advice does the video provide for those who find themselves stuck while trying to verify a trigonometric identity?
-The video advises that if you find yourself stuck while trying to verify a trigonometric identity, you should try making some type of substitution or simplification, even if it might not be immediately apparent if it will help. If the approach complicates the expression further, you can always revert to earlier steps and try a different tactic.

Outlines

00:00

🧮 Introduction to Verifying Trigonometric Identities

The video begins by challenging viewers to solve 14 trigonometric identity problems, encouraging engagement through comments. The instructor demonstrates solving the first problem involving cosecant and cosine functions. The approach emphasizes analyzing the complexity of each side of the identity and utilizing Pythagorean trig identities to simplify expressions. The example starts with converting cosecant squared theta minus one into cotangent squared, followed by further breakdowns and substitutions until proving that the expression simplifies to cosine squared theta.

05:00

🔍 Step-by-Step Solutions for Trigonometric Problems

This section delves deeper into trigonometric identities, tackling a complex problem involving sine and cosine. The instructor uses a systematic approach to combine terms into a single fraction, introduces a common denominator, and simplifies using algebraic manipulations. By breaking down the equation step by step, the problem is reduced to a simpler form that confirms the trigonometric identity. This detailed explanation not only solves the problem but also reinforces the methodical approach needed for verifying trigonometric identities.

10:01

📐 Advanced Techniques for Solving Trigonometric Identities

In this part, more complex trigonometric identities are addressed, using advanced techniques such as substituting with cofunctions and applying even and odd identities. The instructor provides clear explanations of the rationale behind each step, focusing on understanding the properties of trigonometric functions and how to manipulate them effectively. This section is crucial for viewers seeking to deepen their understanding of trigonometric identities and improve their problem-solving skills.

15:02

📏 Exploring Even and Odd Trigonometric Identities

This segment covers the concepts of even and odd functions within trigonometry, particularly focusing on sine and cosine. The instructor uses these identities to solve problems, emphasizing the importance of recognizing and applying these properties to simplify trigonometric equations. The detailed breakdown of each step helps viewers understand how to effectively use these identities to verify complex trigonometric equations.

20:03

🎓 Comprehensive Review and Factorization of Trigonometric Identities

The instructor reviews various trigonometric identities, employing techniques like factorization to simplify and prove the identities. Each example is carefully selected to demonstrate different strategies, such as pulling out common factors or applying Pythagorean identities in novel ways. This comprehensive review helps reinforce the viewers' understanding and ability to handle various trigonometric problems, encouraging them to think critically about each step of the solution process.

25:03

👋 Closing Remarks and Encouragement to Explore More

In the closing remarks, the instructor invites viewers to tackle more trigonometric identities in a subsequent video, aiming to further enhance their understanding and skills. This brief wrap-up not only summarizes the video's content but also motivates viewers to continue practicing and exploring the topic on their own, highlighting the continuous learning journey in mathematics.

Mindmap

Keywords

💡Verifying Trigonometric Identities

Verifying trigonometric identities involves proving that two trigonometric expressions are equivalent using trigonometric formulas, rules, and properties. In the video, the host demonstrates the process of verifying different trigonometric identities, such as proving that cosecant squared theta minus one equals cotangent squared theta over cosecant squared theta equals cosine squared theta. This fundamental concept is central to the video as it guides viewers through a series of step-by-step proofs.

💡Pythagorean Trig Identities

The Pythagorean trigonometric identities are a set of equations derived from the Pythagorean theorem and relate the squares of the sine, cosine, and tangent functions. In the transcript, these identities are frequently referenced to simplify trigonometric expressions or make substitutions during the verification of identities, as seen when converting terms like cosecant squared theta minus one into cotangent squared.

💡Cosecant

Cosecant is the reciprocal of the sine function, expressed as cosec(θ) = 1/sin(θ). In trigonometric identity problems, it is often used to transform and simplify expressions. The video script demonstrates several instances where cosecant is squared and manipulated to prove certain identities, highlighting its utility in advanced trigonometry.

💡Cotangent

Cotangent is a trigonometric function, the reciprocal of the tangent function, represented as cot(θ) = 1/tan(θ) or cot(θ) = cos(θ)/sin(θ). It is pivotal in many identity verifications in the video, such as substituting cotangent squared for other expressions using Pythagorean identities.

💡Conjugate

The concept of conjugate in mathematics typically refers to a pair of expressions that involve the same terms but with opposite operations, such as a+b and a-b. In the video, multiplying by the conjugate is used as a technique to simplify expressions involving square roots or complex numbers, which helps in verifying trigonometric identities.

💡Common Denominator

Finding a common denominator is a technique used in algebra to combine fractions by adjusting them to have the same bottom number or denominator. This method is used in the video to simplify expressions involving fractions, making it easier to verify trigonometric identities, such as combining terms to simplify the verification process.

💡Factorization

Factorization refers to the process of breaking down an expression into simpler multipliers that can be multiplied together to obtain the original expression. In the video, the host uses factorization to simplify complex trigonometric identities, such as factoring out common trigonometric functions from expressions to simplify their forms and facilitate identity verification.

💡Reciprocal Identities

Reciprocal identities in trigonometry involve expressions where trigonometric functions are defined as the reciprocals of other functions, such as sine and cosecant. These identities are extensively used in the video to transform and simplify trigonometric expressions, aiding in the verification of identities by converting one form into another more manageable form.

💡Identity Verification

Identity verification in trigonometry is the process of proving that two trigonometric expressions are equivalent under any angle. This is the central theme of the video, where the host tackles various trigonometric identities, showing step-by-step how each side of the equation can be manipulated to match the other, confirming their equivalence.

💡Pythagorean Theorem

The Pythagorean theorem is a fundamental principle in geometry that relates the lengths of the sides of a right triangle. It's used in trigonometry to derive important identities like the Pythagorean trig identities. In the video, these derived identities are applied to solve and verify complex trigonometric identities by relating the square of the sine and cosine functions to each other and to 1.

Highlights

Introduction to a trigonometric identity verification challenge with 14 problems.

Demonstration of simplifying cosecant squared theta using Pythagorean identities.

Explanation of converting cotangent squared into cosine squared over sine squared.

Step-by-step process of simplifying complex trigonometric expressions by substituting identities.

Technique of multiplying numerators and denominators to simplify trigonometric fractions.

Use of binomial multiplication to simplify expressions involving cosine and sine.

Illustration of verifying an identity by combining fractions and reducing them.

Example of substituting cosecant squared with cotangent squared minus one.

Strategy of making identical substitutions to simplify and prove trigonometric identities.

Encouragement for persistence in solving challenging trigonometric proofs.

Introduction of a method involving the multiplication by conjugates to simplify expressions.

Conversion of cotangent of pi/2 minus theta using cofunction identities.

Verification of identities involving even and odd functions for negative angles.

Application of greatest common factor (GCF) extraction in trigonometric identities.

Final challenge and invitation to further explore trigonometric identities in additional content.

Transcripts

Browse More Related Video

How to Prove Trigonometric Identities (Precalculus - Trigonometry 24)

Ultimate trig identity problem study guide!

Identities Grade 11: Introduction and practice

Verifying Trigonometric Identities

Introduction to Using Trigonometric Identities (Precalculus - Trigonometry 23)

Proving Trigonometric Identities | Fundamental Trigonometric Identities | Formulas | Part 2

Related Tags

Trigonometric Identities Math Challenges Pythagorean Cosecant Cotangent Trigonometry Educational Content Proof Techniques Geometry Mathletics Trig Functions