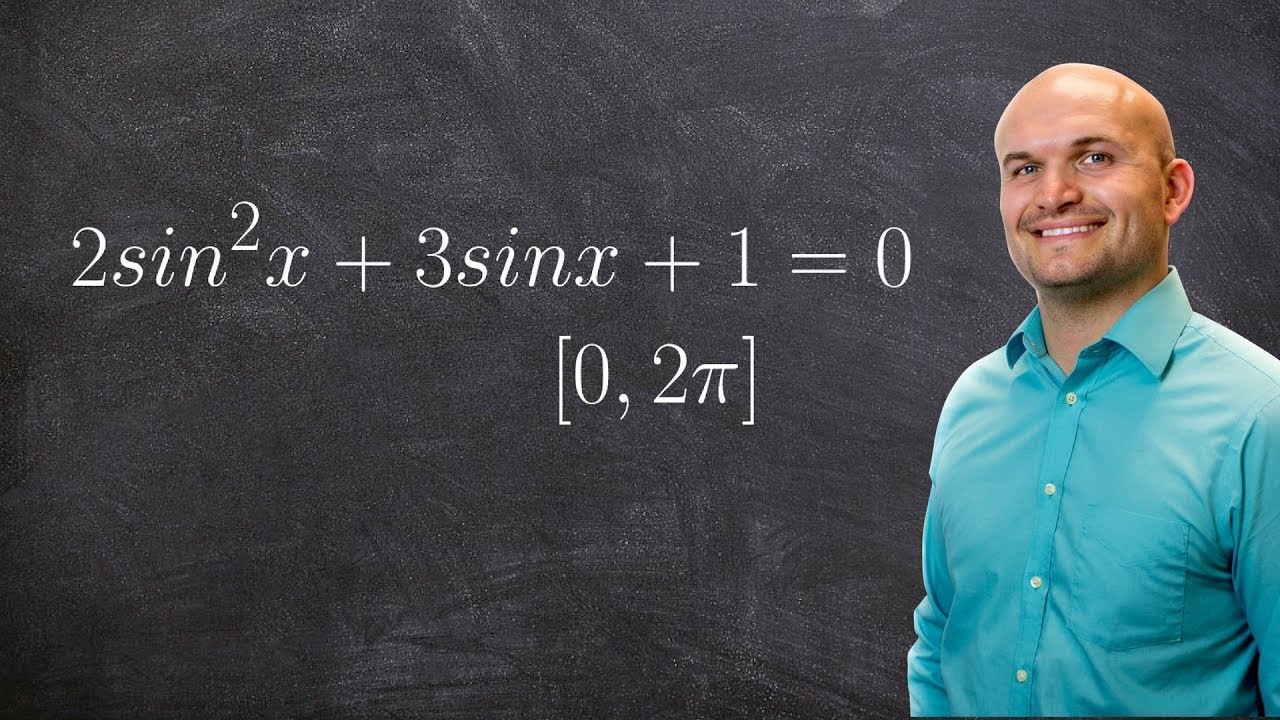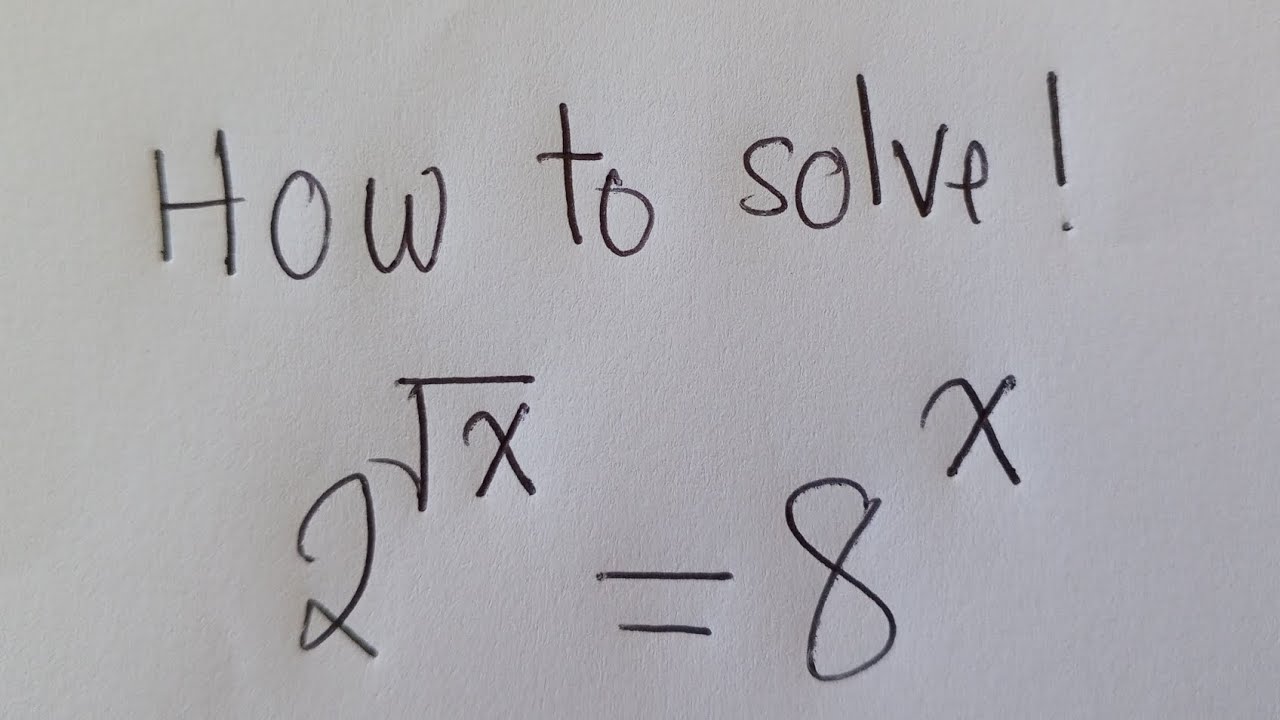Paper 1 common exam questions

Jacob Sichamba Online Math

20 Oct 202318:05

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, the presenter, Chamba Jacob, guides viewers through solving various math problems, including evaluating expressions, simplifying algebraic expressions, factorizing quadratics, and solving equations. He demonstrates the process of evaluating 3^2 + 3^{-1} imes 2^0, simplifies 2(x + 3y) - 3(4x - 2), factors 3x^2 - 207, and illustrates solving a quadratic equation by factoring. Additionally, he explains how to use a Venn diagram to represent set operations and concludes with a problem involving bearings and angles. The video aims to clarify these concepts for learners, encouraging them to engage with the material and apply the techniques presented.

Takeaways

📚 The video is an educational tutorial led by Chamba Jacob, focusing on solving various math problems.
🔢 The first problem involves evaluating an expression with exponents: \(3^2 + 3^{-1} \times 2^0\), which simplifies to \(9 + \frac{1}{3}\) and eventually to \(\frac{28}{3}\) or \(9R1\) over 3.
📈 In the second problem, the task is to simplify an algebraic expression involving brackets: \(2(x + 3y) - (4x - 2)\), resulting in \(-10x + 6y + 6\).
📐 The third problem requires factorizing a quadratic expression: \(3x^2 - 207\), which factors into \(3(x - 9)(x + 3)\) using the difference of squares.
📊 For the fourth problem, a Venn diagram is used to illustrate the union and intersection of sets A, B, and the complement of C, with shading indicating the region where \(A \cup B \cap \complement C\) is true.
🧩 The fifth problem involves solving a quadratic equation: \(2x^2 + x - 3 = 0\), which factors into \((x - 1)(2x + 3) = 0\), yielding solutions \(x = 1\) and \(x = -\frac{3}{2}\).
🔤 In the sixth problem, an exponential equation \(5^{-3x} = 125\) is solved by balancing the bases and equating the powers, resulting in \(x = -1\).
🧭 The final two questions involve bearings, where the bearing of B from A is given as \(035^\circ\) or \(35^\circ\), and the bearing of A from B and C are calculated using geometric properties and angle relationships.
📐 The bearing of A from B is calculated by extending a line and using the Zed property, resulting in \(215^\circ\).
🌐 The bearing of A from C is found by subtracting from \(360^\circ\) after adding the given angles, resulting in \(265^\circ\).
👋 The video concludes with a prompt for viewers to share and like the content, and a goodbye from the presenter, Chamba Jacob.

Q & A

What is the first mathematical operation demonstrated in the video?
-The first mathematical operation demonstrated is the evaluation of the expression 3^2 + 3^-1 * 2^0.
What is the result of the expression 3^2 + 3^-1 * 2^0 after simplification?
-The simplified result of the expression is 9 + 1/3, which further simplifies to 28/3 or 9 with a remainder of 1 over 3.
How does the video approach the simplification of the algebraic expression involving brackets?
-The video approaches simplification by eliminating the brackets and then combining like terms, resulting in -10x + 6y + 6.
What is the common factor used to factorize the expression 3x^2 - 207 in the video?
-The common factor used to factorize the expression is 3, leading to the factorization of 3(x^2 - 9) which further factors into 3(x - 3)(x + 3).
How does the video explain the process of solving a quadratic equation?
-The video explains solving a quadratic equation by finding factors that give the product and sum required, then substituting and factoring by grouping to find the solutions x = 1 and x = -3/2.
What is the method used in the video to solve the equation 5^-3x = 125?
-The method used is to balance the bases by equating the powers, resulting in -3x = 3, and solving for x to get x = -1.
What is the bearing of B from A given in the video?
-The bearing of B from A is given as 035° or 35°.
How does the video calculate the bearing of A from B?
-The video calculates the bearing of A from B by extending the line and using the Zed property, resulting in a bearing of 215°.
What is the method demonstrated in the video to find the bearing of A from C?
-The method demonstrated involves subtracting the bearing of B from A from 90° and then adding the angle ACB, resulting in a bearing of 265°.
What is the main purpose of the video according to the transcript?
-The main purpose of the video is to guide viewers through solving various mathematical problems, including algebraic expressions, quadratic equations, and bearings.

Outlines

00:00

📚 Math Problem Solving Techniques

The first paragraph introduces a video script focused on solving common math exam questions. The speaker, presumably Chamba Jacob, begins with an example of evaluating an expression involving exponents and indices. They demonstrate step-by-step calculations, including simplifying expressions and finding the lowest common denominator to arrive at an answer. The explanation is methodical, emphasizing the importance of following mathematical laws and order of operations.

05:01

🔍 Simplifying Algebraic Expressions

In the second paragraph, the focus shifts to simplifying algebraic expressions. The speaker provides a detailed walkthrough of removing brackets and combining like terms. They show how to multiply the terms outside the brackets with those inside and then simplify the result by grouping similar terms together. The process is explained clearly, with an emphasis on the rules of algebra and the importance of keeping track of signs and coefficients.

10:01

📐 Factorization and Venn Diagrams

The third paragraph covers two topics: factorization and Venn diagrams. For factorization, the speaker explains how to factorize a quadratic expression by identifying common factors and using the difference of squares method. They also discuss solving a Venn diagram problem, which involves identifying the union of sets A and B, the complement of set C, and the intersection of these sets. The explanation includes a step-by-step guide on how to fill in the diagram and identify the correct regions to shade.

15:02

🧩 Solving Quadratic Equations and Exponents

In the fourth paragraph, the speaker tackles solving quadratic equations and working with exponents. They explain the method of factoring to solve a quadratic equation, including finding the product and sum of coefficients, and then finding factors that meet these criteria. Additionally, they demonstrate how to solve an equation involving negative exponents by balancing the bases and equating the powers, leading to the determination of the variable's value.

🗺️ Bearings and Geometric Properties

The final paragraph discusses bearings and geometric properties. The speaker provides a problem involving bearings from different points on level ground, using angles and the properties of a straight line and a circle to find the bearings of points A from B and C. They explain the process of extending lines, using the Zed property, and subtracting from 360° to find the correct bearings. The explanation is practical, applying geometric principles to solve real-world navigation problems.

Mindmap

Keywords

💡Evaluate

To evaluate, in the context of mathematics, means to calculate the value of an expression by performing the necessary operations. In the video, the term is used to describe the process of finding the numerical value of the expression 3^2 + 3^-1 * 2^0. The evaluation leads to the result of 9 + 1/3, which is simplified further in the explanation.

💡Laws of Indices

The laws of indices, also known as the rules of exponents, are mathematical principles that govern the operations of exponentiation. In the video, the laws of indices are applied when simplifying the expression 3^-1 * 2^0, where 3^-1 is 1/3 and 2^0 is 1, according to the zero exponent rule stating any non-zero number raised to the power of zero equals one.

💡Simplify

Simplification in mathematics refers to the process of making a complex expression or equation more straightforward, often by combining like terms or reducing fractions. In the video, the expression 2(x + 3y) - (4x - 2) is simplified by removing brackets and combining like terms, resulting in -10x + 6y + 6.

💡Factorize

Factorization is the process of breaking down a polynomial into a product of its factors. In the script, the term is used when the polynomial 3x^2 - 207 is factorized by taking out the common factor of 3, resulting in 3(x^2 - 9), and then further factorizing using the difference of squares to 3(x - 3)(x + 3).

💡Venn Diagram

A Venn diagram is a visual representation used to show the relationships between sets of numbers or concepts. In the video, a Venn diagram is used to illustrate the union of sets A and B, as well as the intersection of A union B with the complement of C, which helps in visually representing the elements that belong to certain sets.

💡Quadratic Equation

A quadratic equation is a polynomial equation of degree two, typically in the form ax^2 + bx + c = 0. In the video, the quadratic equation 2x^2 + x - 3 = 0 is solved using factorization, where the equation is transformed into (2x + 3)(x - 1) = 0, leading to the solutions x = 1 and x = -3/2.

💡Bearing

In navigation, bearing refers to the direction of a point relative to another, often measured in degrees from north. In the video, bearings are used to describe the directions of points B from A and A from C, using angles such as 035° and 95° to determine the positions of points on a map.

💡Difference of Two Squares

The difference of two squares is a factorization technique used for polynomials that are in the form of a^2 - b^2. In the video, this technique is applied to factorize the expression x^2 - 9 into (x - 3)(x + 3), which is a direct application of the identity a^2 - b^2 = (a - b)(a + b).

💡Exponents

Exponents, also known as powers, indicate how many times a number is multiplied by itself. In the video, exponents are used in expressions like 5^-3x and 5^3, where the bases are raised to different powers to simplify or solve equations, leading to the understanding that 5^-3x = 125 can be simplified by equating the powers and solving for x.

💡Like Terms

Like terms in algebra are terms that have the same variables raised to the same power. In the video, like terms are combined during the simplification process, such as combining -10x and 6y + 6 to form -10x + 6y + 6, which is a standard step in simplifying algebraic expressions.

Highlights

Introduction to solving common paper one exam questions.

Evaluating the expression 3^2 + 3^-1 * 2^0 using laws of indices.

Simplification of the expression using lowest common denominator.

Solving the expression to get 9 remainder 1 over 3.

Simplifying algebraic expressions by removing brackets and combining like terms.

Factorizing quadratic expressions by identifying common factors.

Using the difference of two squares method for complete factorization.

Creating a Venn diagram to visualize set operations.

Identifying the union of sets A and B on the Venn diagram.

Finding the complement of set C and its intersection with the union of A and B.

Shading the region on the Venn diagram to represent the solution.

Solving a quadratic equation by identifying the product and sum.

Finding factors that satisfy the product and sum conditions for the quadratic equation.

Factorizing the quadratic expression by grouping and simplifying.

Solving for the values of x using the factorized form of the quadratic equation.

Solving an exponential equation by balancing the bases and equating the powers.

Determining the bearing of a point from another using geometric properties.

Using the Zed property and angle subtraction to find bearings.

Final solution for the bearing of A from C using circle properties.

Conclusion and invitation to share and like the video.

Transcripts

Browse More Related Video

Sets, Indices, and Algebra Test 1 - JS Learning Academy

Sum and Difference Identities of Sine and Cosine

Solving a trigonometric equation by factoring

Integration Using u-Substitution

Can you solve this? | Exponential Equation | Algebra Problem.

Solving Quadratic Equations By Completing The Square