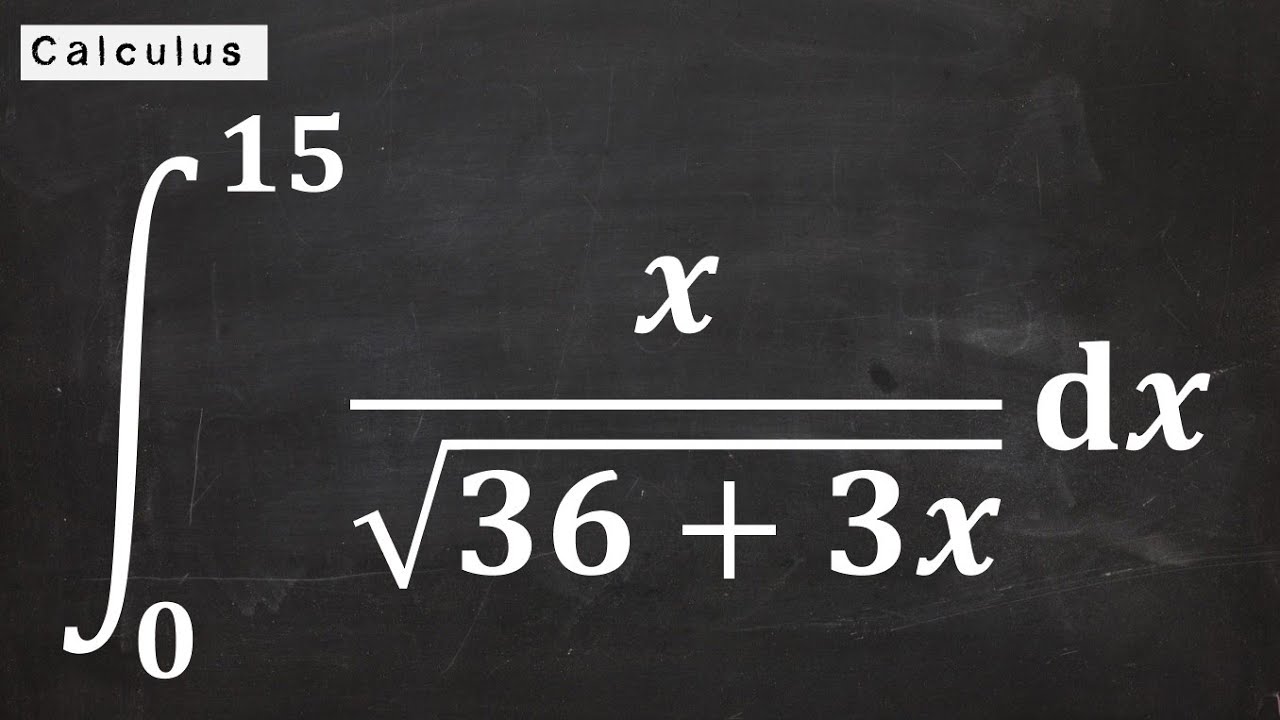Lesson 11 - Integration By Substitution (Calculus 1 Tutor)
TLDRThe video script introduces the concept of integration by substitution, a technique for solving complex integrals that may not have a direct solution. It emphasizes the importance of transforming a difficult integral into a more manageable form by making a suitable substitution, such as letting u be x squared minus one. The script also explains the need to change the variable of integration from dx to du, by taking the derivative of u with respect to x. The goal is to make the integral recognizable and solvable, showcasing the power of substitution in calculus.
Takeaways
- 📚 The course section focuses on integration by substitution, a method for solving integrals that may otherwise seem unsolvable.
- 🌟 Basic integrals with polynomials and trigonometric functions are foundational, but this section goes beyond those to tackle more complex integrals.
- 🔍 The concept of substitution is introduced as a 'trick' to transform challenging integrals into familiar forms.
- 🌌 An example is provided to illustrate the process, integrating a function of x raised to a high power (99th power in this case) using substitution.
- 📈 The integral of x times (x squared - 1) raised to the 99th power is used to demonstrate the application of the substitution method.
- 🔄 The process involves changing the variable of integration from x to another variable, typically denoted as u, and changing the differential from dx to du.
- 👉 The substitution is made by setting u equal to an expression that simplifies the integral, in this case, u = x^2 - 1.
- 🧠 The derivative of u with respect to x (du/dx) is calculated to transform the differential dx into du, which is the key to the substitution process.
- 📊 The derivative of u is found by taking the derivative of the right-hand side of the u expression with respect to x, which for u = x^2 is 2x.
- 🎯 The goal of the substitution method is to make the problem easier to solve by transforming it into a form that can be integrated using known techniques.
- 📚 The script emphasizes the importance of understanding and applying the substitution method for solving complex integrals in calculus.
Q & A
What topic is being discussed in the script?
-The topic being discussed is integration by substitution, a method used to solve integrals that may not have a direct solution.
What is the significance of the substitution method in integration?
-The substitution method is significant because it allows us to transform difficult integrals into forms that we already know how to solve, making the process more manageable and less time-consuming.
What is the basic idea behind the substitution method?
-The basic idea behind the substitution method is to replace the variable of integration and the integrand with other expressions that we can more easily integrate, and then change the differential from dx to du accordingly.
How does one choose the substitution in integration by substitution?
-One chooses the substitution by identifying a part of the integrand that can be represented by a new variable, which simplifies the expression and makes the integration possible.
What is the first step in applying the substitution method?
-The first step in applying the substitution method is to identify a suitable substitution that simplifies the integral, and then replace the original variable with this new variable in the integral expression.
What is the relationship between dx and du in the context of substitution?
-In the context of substitution, dx is the differential with respect to the original variable x, and du is the differential with respect to the new variable u. The relationship between them is established by taking the derivative of u with respect to x, which gives us du/dx, and then we replace dx with du in the integral.
How does the derivative of u with respect to x (du/dx) affect the integration process?
-The derivative of u with respect to x (du/dx) is used to change the differential from dx to du in the integral. This is because when we change the variable of integration, the differential also changes accordingly.
What is an example of an integral that might be difficult to solve without substitution?
-An example of an integral that might be difficult to solve without substitution is ∫(x * (x^2 - 1)^99) dx. This integral is challenging because of the high power in the expression, which would result in a very complex expansion.
What is the purpose of the substitution u = x^2 - 1 in the given script?
-The purpose of the substitution u = x^2 - 1 is to transform the original integral into one where the integrand is a function of u, making it easier to integrate since the expression (x^2 - 1)^99 becomes just u^99.
How does the script suggest we tackle difficult integrals?
-The script suggests that we tackle difficult integrals by using mathematical 'tricks,' such as the substitution method, to transform the problem into a form that we already know how to solve.
What is the final goal of using the substitution method?
-The final goal of using the substitution method is to obtain the answer to the original integral by solving the transformed integral, which is easier to handle and compute.
Outlines
📚 Introduction to Integration by Substitution
This paragraph introduces the concept of integration by substitution, a technique used to solve integrals that may not have a straightforward solution. The speaker explains that after learning basic integrals involving trigonometric functions and polynomials, students will encounter more complex integrals that require the use of tricks. The first trick discussed is substitution, which involves transforming a difficult integral into a form that is already familiar. The speaker uses the example of integrating a function involving x squared minus 1 raised to the 99th power to illustrate the process of substitution, emphasizing that this method can simplify the problem and make it solvable.
Mindmap
Keywords
💡Integration
💡Substitution
💡Trigonometric Functions
💡Polynomials
💡x squared
💡Formula
💡Variable
💡Derivative
💡Integral of x times x squared minus 1 to the 99th power
💡U equals x squared minus one
💡dU/dX
Highlights
Introduction to integration by substitution as a method for solving complex integrals.
Explanation of how basic integrals with trigonometric functions and polynomials are taught initially.
Discussion on the challenge of integrating expressions like x squared when raised to a high power, such as the 99th power.
Emphasis on the need for employing tricks to solve integrals that do not have known solutions.
The concept of substitution to transform a difficult integral into a solvable form.
Illustration of the substitution method through an example involving the integral of x times (x squared - 1) raised to the 99th power.
Explanation of how to make a substitution in the integral by setting u as x squared - 1.
Clarification on the process of transforming the integrand and the differential from dx to du.
Demonstration of finding du/dx by taking the derivative of u with respect to x, similar to the derivative of y in y = x squared.
The importance of understanding the derivative of the substitution variable to transform the differential dx into du.
The method of integration by substitution as a powerful tool for tackling integrals that seem unsolvable at first glance.
The potential of the substitution method to simplify complex integrals and make them manageable.
The necessity of learning and applying mathematical tricks to expand one's ability to solve a variety of integrals.
The transformative power of mathematical substitution to convert a seemingly intractable problem into a familiar, solvable one.
The practical application of the substitution method in calculus to solve integrals that do not have direct formulas.
The step-by-step process of applying the substitution method, from identifying the substitution variable to transforming the integrand and differential.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: