Another u-subsitution example
TLDRIn this video, the presenter tackles an indefinite integral involving the sine and cosine functions, specifically the integral of sin(x) divided by the square of cos(x). The solution process is methodically explained using the technique of u-substitution, where u is defined as cos(x), and du/dx is derived as -sin(x). By substituting and simplifying, the integral is transformed into a more manageable form, and the antiderivative is found to be 1/cos(x) + C. The video is a clear demonstration of problem-solving in calculus, emphasizing the power of substitution to simplify complex integrals.
Takeaways
- 📚 The problem discussed is the indefinite integral of sin(x)/(cos(x)^2) dx, which can also be written as sin(x)/cos^2(x) dx.
- 🔄 U-substitution is the method used to solve this integral, identified by recognizing a pattern where the derivative of the integrand's base function is present.
- 🎯 The substitution u = cos(x) is chosen, with du/dx = -sin(x), which helps transform the original integral into a more manageable form.
- ✍️ After substitution, the integral becomes -∫(1/u^2) du, which is a standard form that can be easily integrated.
- 📈 The antiderivative of 1/u^2 is -1/u, which is found by applying the power rule for integration (increasing the exponent by 1 and dividing by the new exponent).
- 🔄 The result of the integral is -1/u + C, but due to the negative sign from the substitution, the final answer is 1/u + C.
- 🌐 The final answer is expressed in terms of the original variable x by substituting back u = cos(x), resulting in 1/cos(x) + C.
- 📊 The process demonstrates the power of u-substitution in simplifying complex integrals by transforming them into more recognizable and manageable forms.
- 🤔 The script emphasizes the importance of recognizing when to use u-substitution, particularly when the derivative of the integrand's function is evident.
- 📚 The video script serves as an educational resource for those learning about integration techniques and provides a step-by-step walkthrough of a specific problem.
- 🎓 The explanation is detailed and methodical, ensuring that viewers can follow along and understand the reasoning behind each step of the solution.
Q & A
What is the integral being discussed in the transcript?
-The integral being discussed is the indefinite integral of sin(x)/(cos(x)^2) dx.
What is the significance of recognizing a pattern in the integral?
-Recognizing a pattern in the integral is crucial because it helps identify the appropriate method for solving it, such as u-substitution in this case.
What is u-substitution in integration?
-U-substitution is a technique used in integration where a variable is introduced (u) to simplify the integral by making it easier to find its antiderivative.
How does the derivative of u with respect to x (du/dx) relate to the original function in the integral?
-In this case, if u is equal to the cosine of x, then du/dx is equal to -sin(x), which is the derivative of the cosine function.
What is the purpose of multiplying and dividing by the same value in the integral?
-Multiplying and dividing by the same value, in this case -1, is done to simplify the integral and make it easier to work with, particularly to match the form needed for u-substitution.
What is the antiderivative of x to the power of -2?
-The antiderivative of x to the power of -2 is 1/(x^2), which simplifies to the negative of 1/(x^(-1)) or negative of the reciprocal of x.
How does the substitution u = cos(x) transform the original integral?
-After substituting u = cos(x), the original integral sin(x)/(cos(x)^2) dx becomes -1/u^2 du, which simplifies the process of finding the antiderivative.
What is the final result of the integral after applying u-substitution?
-The final result of the integral after applying u-substitution and simplifying is 1/u + C, where u = cos(x), so the result is 1/cos(x) + C.
What is the role of the constant C in the antiderivative?
-The constant C represents the constant of integration, which is added to the antiderivative to account for the infinite number of possible antiderivatives that can be formed from a given derivative.
Why is it important to verify the result by taking the derivative?
-Verifying the result by taking the derivative is important to ensure that the found antiderivative is correct, as the derivative should match the original function when the substitution is reversed.
Outlines
📚 Introduction to u-Substitution and Problem Setup
The speaker begins by expressing enthusiasm for u-substitution problems, noting that they help build momentum for tackling more complex tasks. The specific problem introduced involves finding the indefinite integral of sin(x) divided by the square of cos(x), or equivalently, sin(x) over cos^2(x). The speaker emphasizes the importance of recognizing when to use u-substitution, particularly when the function and its derivative are evident in the integral. The explanation proceeds with a step-by-step breakdown of how to approach the integral, mentioning the known method for integrating x^(-2) and the process of increasing the exponent by one and then applying the new exponent rule. The speaker also points out the pattern in the problem that suggests using u-substitution, specifically the presence of cos(x) and its derivative, sin(x).
🔄 Executing u-Substitution and Solving the Integral
Continuing from the previous paragraph, the speaker executes the u-substitution by setting u equal to cos(x) and then deriving it with respect to x, resulting in du = -sin(x)dx. The integral is then rewritten in terms of u, transforming sin(x)dx into -du. The speaker simplifies the integral to -1/u^2 du, which is equivalent to -u^(-1) du, and then applies the exponent rule to find the antiderivative, resulting in -1/u plus a constant (c). The speaker clarifies that the negative sign from the integral and the one in the antiderivative cancel each other out, leaving 1/u + c as the final answer. Finally, the speaker substitutes back u = cos(x) to obtain the antiderivative of the original problem, which is 1/cos(x) + c, and concludes the explanation, indicating a continuation in the next video.
Mindmap
Keywords
💡u substitution
💡indefinite integral
💡antiderivative
💡derivative
💡cosine of x
💡sine of x
💡integration by substitution
💡momentum
💡preparation
💡ambiguous
💡exponent
💡plus c
Highlights
Evan from Norway requested another u-substitution problem.
The problem involves the indefinite integral of sin(x) over cos(x)^2 dx.
The integral can also be written as sin(x) over cos^2(x).
The strategy is to look for patterns where the derivative of the integrand is visible.
The integral 1/x^2 dx is equivalent to the antiderivative of x^(-2).
The process involves increasing the exponent by 1 and dividing by the new exponent.
The derivative of cos(x) is -sin(x), which is crucial for the u-substitution.
Substitute u for cos(x), with du/dx = -sin(x) and du = -sin(x)dx.
The integral can be rewritten as -∫sin(x)dx over cos(x)^2 by multiplying by -1.
After substitution, the integral simplifies to -1/u^2 du.
The antiderivative of -1/u^2 is u^(-1), which is equivalent to 1/u.
The negative sign outside the integral simplifies the expression.
The final antiderivative is 1/u + C, where u is cos(x).
The solution is presented in a step-by-step manner for clarity.
The method demonstrates the power of u-substitution in simplifying complex integrals.
The video aims to build momentum for tackling more complex problems.
The explanation is engaging and accessible, making it suitable for various audiences.
Transcripts
Browse More Related Video

Antidifferentiation by substitution | MIT 18.01SC Single Variable Calculus, Fall 2010
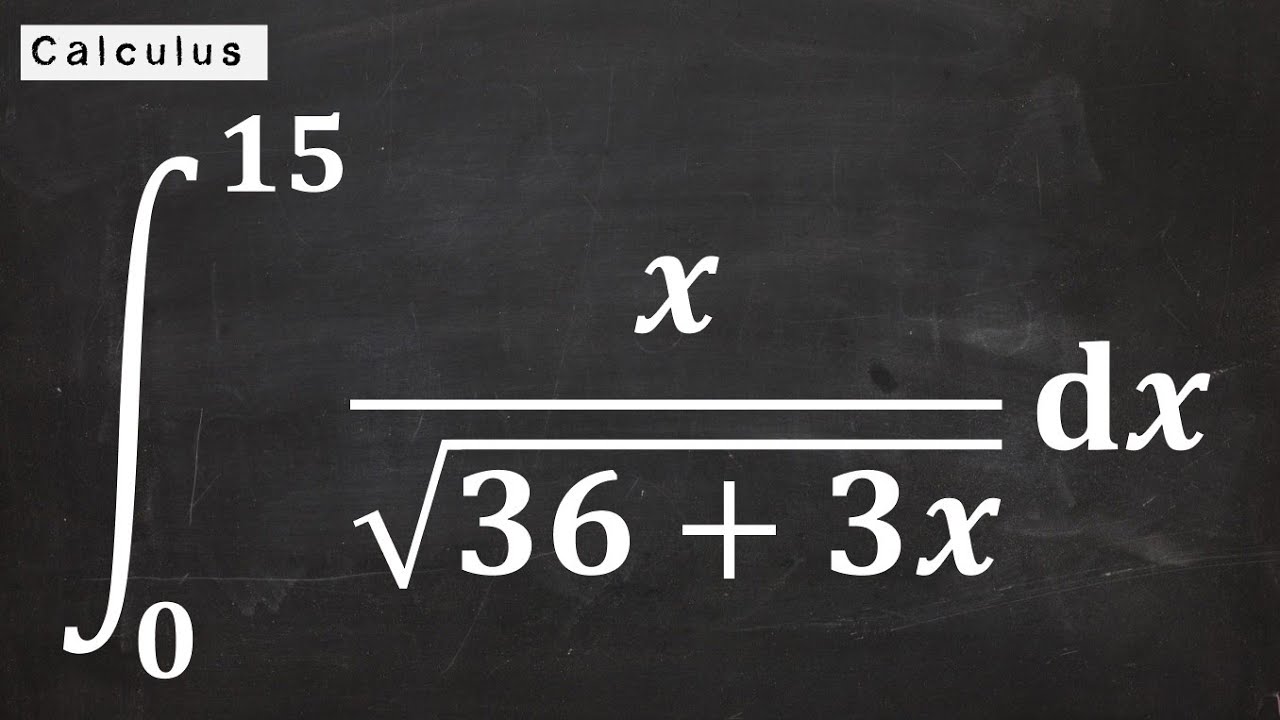
Definite Integral With U-Substitution

_-substitution: logarithmic function | AP Calculus AB | Khan Academy

Lesson 11 - Integration By Substitution (Calculus 1 Tutor)

(2^ln x)/x Antiderivative Example

Integration Using The Substitution Rule
5.0 / 5 (0 votes)
Thanks for rating: