Calculus AB Lesson 6.7: U-Substitution

Michelle Krummel

25 Feb 201841:54

EducationalLearning

32 Likes 10 Comments

TLDRThis video tutorial introduces the integration technique known as u-substitution, demonstrating how to integrate composite functions through a series of examples. The instructor guides viewers through the process of identifying the inside function, taking derivatives, and making substitutions to simplify the integral. The script covers various examples, including definite integrals, and emphasizes the importance of checking answers by differentiating the result. The goal is to help learners master u-substitution for solving complex integrals.

Takeaways

📚 The video discusses an integration technique known as 'u-substitution' for solving integrals of composite functions.
🔍 The process begins with 'guess and check' to identify the function whose integral will give the derivative of the integrand.
🌟 The integral of cosine(x) is sine(x) plus a constant C, which is derived by recognizing the derivative of sine(x) as cosine(x).
🔄 For integrals involving composite functions, such as cosine(3x), the technique involves multiplying by the derivative of the inner function and adjusting for constants.
📈 The video demonstrates how to integrate more complex expressions by identifying the inner function (u) and its derivative (du/dx), then rewriting the integral in terms of u.
📝 The method involves rewriting the integral to eliminate x and replace it with u, and then integrating with respect to u using standard integration techniques.
📉 After integrating with respect to u, the final step is to substitute back the original variable (x) to express the integral in terms of the original function.
📌 The video provides several examples, including integrating 2x over x squared plus 3, and x over the square root of x squared plus 3, to illustrate the u-substitution method.
📑 The script emphasizes the importance of correctly choosing the inner function (u) for successful u-substitution, as an incorrect choice can lead to a dead end.
📝 The technique is also applied to definite integrals, where the bounds of integration must be adjusted according to the substitution made for u.
📚 The video concludes with practice problems for the viewer to apply the u-substitution method, reinforcing the concepts taught.

Q & A

What is the integral technique discussed in the video?
-The video discusses the integration technique called 'u-substitution' for integrating composite functions.
What is the integral of cosine x in terms of sine x?
-The integral of cosine x is sine x plus C, where C is the constant of integration.
How do you find the integral of cosine 3x using u-substitution?
-You set u to be 3x, find the derivative du/dx which is 3, and then the integral of cosine 3x becomes (1/3) sine 3x plus C.
What is the integral of 3 cosine 3x dx?
-The integral of 3 cosine 3x dx is essentially 3 times the integral of cosine 3x dx, which is sine 3x plus C.
What is the process of u-substitution for integration?
-The process involves identifying the inside function as u, finding its derivative du/dx, rewriting the integral in terms of u and du, and then integrating with respect to u.
How does the chain rule apply to integration with composite functions?
-The chain rule is used to differentiate composite functions. When integrating, you work backwards from the derivative to the original function, effectively 'undoing' the chain rule.
What is the integral of 2x times the cube root of x squared plus 5 with respect to x?
-After setting u to x squared plus 5 and finding du/dx, the integral becomes 3/4 times u to the 4/3 plus C, and substituting back, it's 3/4 times (x squared plus 5) to the 4/3 plus C.
How do you handle the integral of 2x over x squared plus 3?
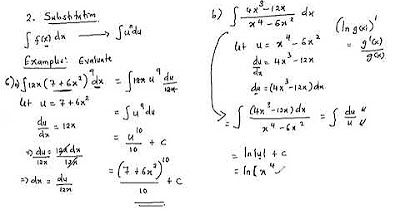
-By setting u to x squared plus 3, the integral simplifies to 1 over u du, which integrates to the natural log of the absolute value of u plus C, and substituting back gives ln|x squared plus 3| plus C.
What is the integral of x over the square root of x squared plus 3?
-After setting u to x squared plus 3, the integral becomes 1/2 du over the square root of u, which integrates to 2/3 times u to the 3/2 plus C, and substituting back gives 2/3 times (x squared plus 3) to the 3/2 plus C.
How does the video script guide through the integration of e to the cosine x times sine x dx?
-By setting u to cosine x, the integral becomes e to the u times negative du, which integrates to negative e to the u plus C, and substituting back gives negative e to the cosine x plus C.
What is the approach for the definite integral of x times the square root of 2x plus 1?
-The approach is similar to the indefinite integral, but with attention to changing the bounds of integration from x values to u values after substitution.
How does the video demonstrate the importance of choosing the right u for u-substitution?
-The video demonstrates by showing that choosing the wrong inside function can lead to complications in integration, and suggests going back and trying a different function if one gets stuck.
What is the final answer for the integral of 2x plus 1 over the square root of x plus 4?
-After substitution and simplification, the integral evaluates to 4/3 times (x plus 4) to the 3/2 minus 14 times (x plus 4) to the 1/2 plus C.
How does the video script handle the evaluation of definite integrals?
-The script shows that for definite integrals, after substitution, you evaluate the antiderivative at the new bounds in terms of u, and then substitute the original x values back in to get the final answer.

Outlines

00:00

📚 Introduction to Integration by Substitution

This paragraph introduces the concept of integration by substitution, using the integral of cosine x, cosine 3x, and 3 cosine 3x as an example. The process begins with a 'guess and check' method to find the antiderivative of cosine x, which is sine x plus C. The speaker then explains how to handle composite functions, such as cosine 3x, by adjusting the antiderivative of sine 3x to account for the chain rule in differentiation. The paragraph concludes with a general approach to integrating composite functions by identifying the inside function, setting it as 'u', and then finding du/dx to rewrite the integral in terms of 'u' and dx.

05:03

🔍 Step-by-Step Integration Process

The second paragraph delves into a systematic approach to integration, emphasizing the importance of identifying the inside function 'u' and its derivative du/dx. It illustrates the process with an example of integrating 2x times the cube root of (x squared plus 5) with respect to x. The speaker shows how to substitute u for the inside function, replace dx with du, and then integrate using standard rules. The summary also includes a brief mention of an example where the inside function is chosen as the denominator of a fraction, highlighting the need to consider the derivative of the chosen 'u'.

10:03

🔧 Adjusting for Composite Functions in Integration

This paragraph continues the discussion on integrating composite functions, focusing on the need to adjust the antiderivative when the derivative of the inside function is present in the integral. The speaker uses the example of integrating x over the square root of x squared plus 3, choosing x squared plus 3 as 'u' and its derivative as 2x. The explanation includes the steps of rewriting the integral in terms of 'u', substituting dx with du, and simplifying the expression before integrating.

15:05

📉 Integration with Exponential and Trigonometric Functions

The fourth paragraph addresses the integration of a function involving an exponential and a trigonometric function, e to the cosine x times sine x. The speaker chooses cosine x as 'u' and its derivative negative sine x to facilitate the substitution. The integral is then simplified by replacing dx with du and integrating e to the power of 'u', resulting in the antiderivative e to the power of 'u'. The final step is to substitute back to the original variable to complete the integration.

20:06

📝 Working Through Integration Examples

In this paragraph, the speaker provides a series of integration examples, guiding the viewer through the process of choosing the inside function 'u', taking its derivative, and making the necessary substitutions to rewrite the integral in terms of 'u'. Each example illustrates a different scenario, such as dealing with a cubic term, an exponential function, and a quotient that requires simplification before integration. The speaker emphasizes the importance of simplifying the integral to a form that can be easily integrated using known rules.

25:08

📌 Definite Integrals and Variable Substitution

The sixth paragraph introduces the concept of definite integrals, where the bounds of integration are specified. The speaker demonstrates how to choose an appropriate 'u', make the derivative substitution, and adjust the bounds according to the new variable. The example involves integrating x times the square root of (2x plus 1) from x=0 to x=1, with 'u' chosen as 2x plus 1. The process includes rewriting the integral in terms of 'u', adjusting the bounds, and simplifying the expression before integrating.

30:13

🧩 Solving Definite Integrals with Variable Bounds

This paragraph continues the discussion on definite integrals, emphasizing the need to correctly identify the bounds in terms of the new variable 'u'. The speaker uses an example of integrating x over the square root of (x plus 4) from x=-1/2 to x=0, choosing x plus 4 as 'u'. The explanation covers the steps of finding the derivative, substituting dx with du, and evaluating the integral at the new bounds. The final answer is simplified to provide the definite integral's value.

35:14

📘 Conclusion and Practice Problems

The final paragraph concludes the video script by summarizing the integration process and encouraging viewers to practice the technique with provided problems. The speaker briefly works through six practice problems, demonstrating the application of the integration by substitution method. Each problem is solved by identifying the inside function, making the appropriate substitutions, and integrating to find the antiderivative. The solutions are presented in a concise manner, highlighting the steps taken to arrive at the final answers.

Mindmap

Keywords

💡Integration Technique

Integration techniques are methods used to find the integral or antiderivative of a function. In the context of the video, the focus is on 'u-substitution,' a technique that simplifies the integration of composite functions by substituting a new variable to make the integral more manageable. The video demonstrates this technique through various examples, such as integrating functions involving cosine and exponential expressions.

💡Composite Function

A composite function is a function composed of two or more functions, such as f(g(x)). In the script, composite functions are integrals that have an inner function and an outer function, where the derivative of the inner function is part of the original integrand. The video discusses how to integrate such functions using u-substitution, identifying the inner function as 'u' and then performing the integration.

💡Derivative

The derivative of a function represents the rate of change of the function with respect to its variable. In the script, derivatives are used to identify the inside function for u-substitution and to check the correctness of the antiderivative found. For example, the derivative of sine(x) is cosine(x), which is used to establish the relationship between the integral and the function to be integrated.

💡U-Substitution

U-substitution is a specific integration technique where a part of the integrand is replaced with a new variable 'u' to simplify the integral. The video script provides a step-by-step process for u-substitution, including identifying the inside function, finding its derivative, and rewriting the integral in terms of 'u' before integrating.

💡Chain Rule

The chain rule is a fundamental calculus rule used to find the derivative of a composite function. In the context of u-substitution, the chain rule is used in reverse to break down the integral into simpler components. The video explains that when differentiating a composite function, the chain rule is applied, and when integrating, the process essentially 'undoes' the chain rule.

💡Antiderivative

An antiderivative, also known as an integral, is a function that represents the reverse process of differentiation. The script discusses finding antiderivatives of various functions as part of the u-substitution process. For instance, the antiderivative of sine(x) is -cosine(x) + C, where 'C' is the constant of integration.

💡Constant of Integration

The constant of integration, typically denoted by 'C', is added to an antiderivative to account for the infinite number of functions that could result from an indefinite integration. In the script, 'C' is included in the final answer of each integral to indicate that the solution is a family of functions that are all shifted vertically by some constant amount.

💡Definite Integral

A definite integral is an integral that calculates the exact value of the area under the curve of a function between two specified points. The script includes an example of a definite integral where the bounds are changed to 'u' values after substitution, and the integral is evaluated between these new bounds.

💡Indefinite Integral

An indefinite integral is an antiderivative without specified bounds, representing a family of functions that differ by a constant. The video script primarily focuses on indefinite integrals, showing the process of finding them through u-substitution and emphasizing the inclusion of the constant of integration 'C'.

💡Power Rule

The power rule is a basic integration rule that states the integral of x^n, where n is a constant, is x^(n+1)/(n+1) + C. In the script, the power rule is used for integrating expressions in terms of 'u' after the substitution process, simplifying the integration of polynomial and root functions.

Highlights

Introduction to the integration technique called 'u-substitution'.

Demonstration of integrating the function cosine x using sine x plus C as the integral.

Explanation of integrating composite functions using the derivative of the inner function.

Integration of cosine 3x by multiplying 1/3 and using the chain rule.

Integration of a function with both the function and its derivative present, resulting in sine 3x plus C.

Use of the chain rule in reverse for integration to undo the differentiation process.

Step-by-step process for integrating composite functions, starting with identifying the inner function 'u'.

Rewriting the integral in terms of 'u' and substituting DX with an expression involving 'u'.

Integration of 2x times the cube root of x squared plus 5 using substitution and power rule.

Dealing with the integral of 2x over x squared plus 3 by choosing the denominator as 'u'.

Integration of x over the square root of x squared plus 3 using a suitable 'u' substitution.

Guidance on choosing the right 'u' for integration and the importance of checking with the derivative.

Integration of e to the cosine x sine x DX using 'u' substitution with careful attention to the chain rule.

Solving for X in terms of 'u' to facilitate substitution in complex integrals.

Integration of a quotient involving 2x plus 1 over the square root of x plus 4 using 'u' substitution.

Dealing with definite integrals by changing the bounds in terms of 'u' and performing the integration.

Practical examples of 'u' substitution with various functions to practice the technique.

Emphasis on the importance of simplifying the integral before applying the power rule.

Final summary of the 'u' substitution method and its application in integral calculus.

Transcripts

Browse More Related Video

Calculus 1: U-Substitution Examples

U-Substitution

Changing the Order of Integration (Double Integrals)

4.6 - Integration Techniques - Integration by Parts

Advanced Strategy for Integration in Calculus

Integration using substitution method

Related Tags

Calculus Integration Youth Substitution Composite Functions Derivative Integral Techniques Chain Rule Math Education Problem Solving Educational Content