Math Antics - Adding and Subtracting Fractions
TLDRIn this Math Antics video, we explore the correct way to add fractions, debunking the misconception that adding numerators and denominators independently will yield the correct result. The video humorously demonstrates that this approach violates the 'Order of Operations' rule, which prioritizes multiplication and division over addition and subtraction. To add fractions with the same denominator, simply add the numerators and keep the denominator the same. The process is illustrated with examples, such as adding 1/2 and 1/2 to get a whole, and 5/16 plus 2/16 to get 7/16. The video also touches on subtracting 'like' fractions and hints at the next lesson, which will cover adding 'unlike' fractions by finding a common denominator.
Takeaways
- 📚 The video discusses the basics of adding fractions, suggesting a different approach than traditional math books.
- 🔄 Math Antics recommends learning multiplication of fractions before addition, due to its simplicity.
- ❌ Attempting to add fractions by simply summing the numerators and denominators separately is incorrect.
- 🚫 The script highlights the 'Order of Operations' rule, emphasizing that multiplication and division must come before addition and subtraction.
- 📉 Adding the numerators and denominators of fractions separately breaks the Order of Operations rule by performing addition before division.
- 🔑 A trick for adding fractions with the same denominators is introduced, which involves only adding the numerators while keeping the denominator constant.
- 🌰 The video provides examples, such as adding 1/2 + 1/2 to get 2/2, which simplifies to a whole.
- 🔢 For fractions with the same denominators, the process of addition (and subtraction) is straightforward: add (or subtract) the numerators and keep the denominator the same.
- ➖ Subtracting fractions with the same denominators follows the same principle as addition: subtract the numerators and retain the denominator.
- 🔄 The term 'Like Fractions' is used to describe fractions with the same denominators, which can be easily added or subtracted using the trick.
- 🤔 The video ends with a teaser for the next lesson, which will cover how to find a common denominator to add or subtract 'Unlike Fractions' with different denominators.
Q & A
Why does Math Antics suggest learning to multiply fractions before adding them?
-Math Antics suggests learning to multiply fractions before adding them because multiplication of fractions is simpler and more intuitive, involving just multiplying the numerators together and the denominators together.
What is the incorrect method shown in the video for adding fractions?
-The incorrect method shown is adding the numerators together and the denominators together without considering the order of operations, which leads to an incorrect result.
What mathematical rule is broken by adding the numerators and denominators of fractions directly?
-The rule broken is the 'Order of Operations', which states that multiplication and division should be performed before addition and subtraction.
Why can't we add fractions by simply adding their numerators and denominators?
-We can't add fractions by simply adding their numerators and denominators because fractions represent division, and the order of operations must be followed to maintain mathematical accuracy.
What is the trick to add fractions without dividing when they have the same denominator?
-The trick is to add the numerators of the fractions while keeping the same denominator, which is possible because it adheres to the order of operations and simplifies the process.
What is the result of adding 1/2 and 1/2 using the correct method?
-The result of adding 1/2 and 1/2 using the correct method is 2/2, which simplifies to 1, representing a whole.
How do you add fractions with the same denominator?
-To add fractions with the same denominator, you add their numerators and keep the denominator the same.
What is the term used for fractions with the same denominator?
-Fractions with the same denominator are called 'like' fractions.
How does the process of adding 'like' fractions differ from adding 'unlike' fractions?
-Adding 'like' fractions is straightforward by just adding their numerators. In contrast, adding 'unlike' fractions requires finding a common denominator to convert them into 'like' fractions before addition.
What is the term for fractions with different denominators?
-Fractions with different denominators are referred to as 'unlike' fractions.
What must be done to add 'unlike' fractions without performing division first?
-To add 'unlike' fractions without performing division first, you need to find a common denominator to convert the 'unlike' fractions into 'like' fractions.
What is the term for the bottom number of a fraction in mathematical language?
-The term for the bottom number of a fraction in mathematical language is 'denominator'.
What is the next step in learning to add fractions after understanding 'like' fractions?
-The next step is to learn how to find a common denominator to add or subtract 'unlike' fractions.
Outlines
📚 Understanding Fraction Addition Basics
This paragraph introduces the concept of adding fractions and challenges the traditional teaching order by suggesting multiplication should be learned before addition. It humorously demonstrates an incorrect method of adding fractions by simply adding numerators and denominators, leading to a contradiction. The speaker clarifies the mistake by explaining the 'Order of Operations' rule, which prioritizes multiplication and division over addition and subtraction. The paragraph concludes by introducing a method to add fractions with the same denominators by adding only the numerators, keeping the denominator constant, and provides examples to illustrate this process.
🔢 Adding Fractions with the Same Denominator
This section delves into the process of adding fractions that share the same denominator, which is a straightforward method involving the addition of numerators while keeping the denominator unchanged. The paragraph provides a step-by-step example, adding one-half to another one-half, resulting in a whole. It further illustrates this with the addition of 5/16 and 2/16, resulting in 7/16. The concept is extended to subtraction of fractions with the same denominator, using 5/9 minus 2/9 as an example, which simplifies to 3/9 or 1/3 after simplification. The term 'Like Fractions' is introduced for fractions with identical denominators, and the paragraph ends with a light-hearted joke about the term's origin.
🤔 Adding Unlike Fractions: Finding a Common Denominator
The final paragraph addresses the challenge of adding fractions with different denominators, which cannot be directly added using the previously mentioned trick. It explains that to add 'unlike' fractions, one must first convert them into 'like' fractions by finding a common denominator. This process is essential before applying the addition method for fractions with the same denominator. The paragraph teases the next video, which will cover how to find a common denominator, and encourages viewers to practice the exercises provided in the current section. It concludes by directing viewers to www.mathantics.com for more information.
Mindmap
Keywords
💡Fractions
💡Numerator
💡Denominator
💡Order of Operations
💡Like Fractions
💡Unlike Fractions
💡Common Denominator
💡Multiplication of Fractions
💡Simplification
💡Math Antics
Highlights
Math Antics suggests learning to multiply fractions before adding them.
Multiplication of fractions is straightforward: multiply the numerators and denominators separately.
Attempting to add fractions by simply adding numerators and denominators leads to incorrect results.
Adding 1/2 and 1/2 incorrectly results in 2/4, which simplifies to 1/2, not a whole.
The 'Order of Operations' dictates that multiplication and division must be done before addition and subtraction.
Fractions represent division, so adding numerators and denominators breaks the rules of order.
A trick exists to add fractions without dividing, but it only works for fractions with the same denominator.
To add fractions with the same denominator, add the numerators and keep the same denominator.
Adding 1/2 and 1/2 correctly results in 2/2, which simplifies to a whole.
Adding fractions with the same denominator is demonstrated with the example 5/16 + 2/16 = 7/16.
Subtraction of fractions with the same denominator works similarly by subtracting the numerators.
Subtracting 5/9 - 2/9 results in 3/9, which simplifies to 1/3.
Fractions with the same denominator are called 'like' fractions and are easy to add or subtract.
The term 'like' fractions is humorously attributed to the fractions 'liking' each other.
To add 'unlike' fractions, they must first be converted into 'like' fractions by finding a common denominator.
A common denominator is necessary to add or subtract fractions with different denominators.
The process of finding a common denominator will be explained in the next video.
The video encourages viewers to complete exercises to reinforce the learning of adding and subtracting fractions.
More information and resources can be found at www.mathantics.com.
Transcripts
Browse More Related Video

Addition and Subtraction of Fractions

Math Antics - Common Denominator LCD

Multiplication and Division of Fractions

Rational Expressions Review
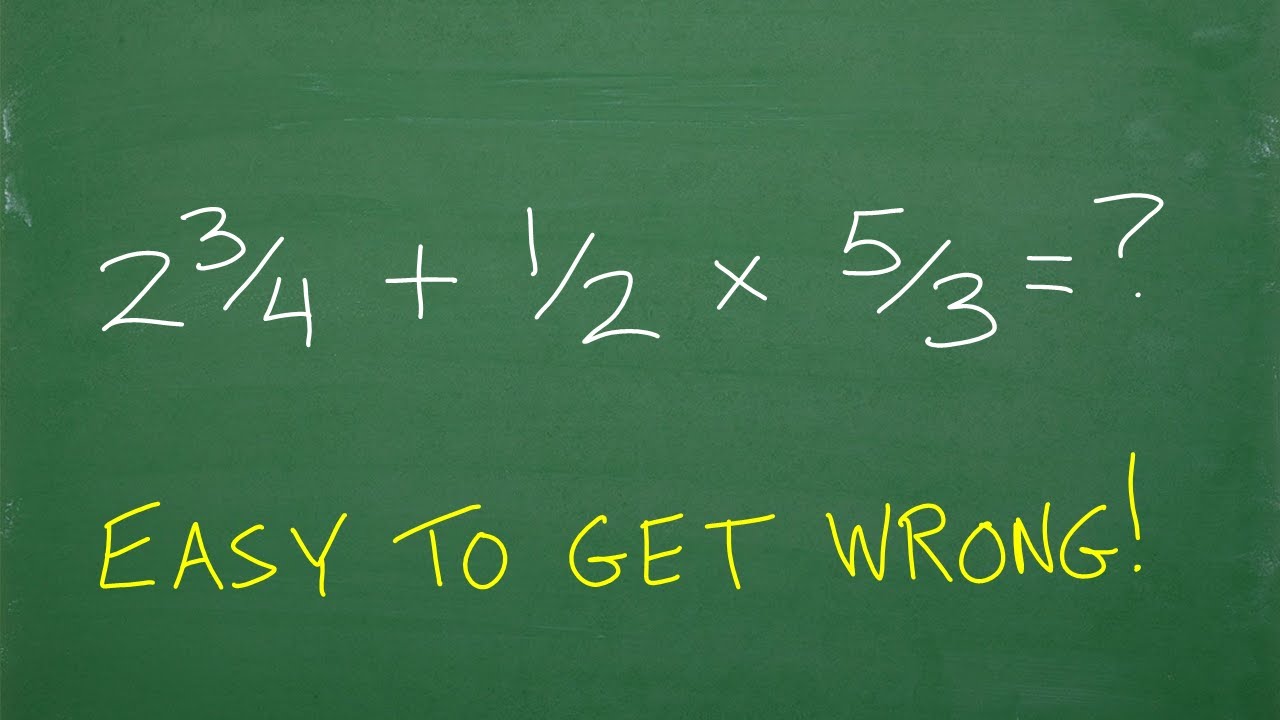
(2 and 3/4) plus 1/2 times 5/3 = ? What’s the first thing you should be thinking in this problem?

Manipulating Rational Expressions: Simplification and Operations
5.0 / 5 (0 votes)
Thanks for rating: