AP Physics 1 Kinematics Review
TLDRThe video script is an in-depth review of kinematics, focusing on the concepts of vectors, scalars, position, distance, displacement, and the differences between them. It explains velocity and acceleration, emphasizing their relationship with displacement and distance traveled. The script further delves into uniformly accelerated motion, particularly freefall and projectile motion, detailing how to analyze and graph these motions. It highlights the importance of understanding the components of vectors and the application of kinematic equations to solve physics problems.
Takeaways
- 📚 Kinematics is the study of motion without considering the causes, focusing on vectors (magnitude and direction) and scalars (magnitude only).
- 📍 A coordinate system is used in physics to track the positions of objects, with defined positive directions like the XY plane.
- 🛤️ Distance is the total length of the path traveled, while displacement is the straight-line distance from the initial to the final position, independent of the path taken.
- 📏 The base unit for both distance and displacement is the meter, and displacement includes direction, making it a vector quantity.
- 🚶♂️ Speed is the total distance traveled over time, measured in meters per second, and is a scalar quantity.
- 🏃♀️ Velocity is the displacement over time and includes both magnitude and direction, making it a vector quantity.
- 🔄 Average acceleration is the change in velocity divided by the time taken, and it describes the rate of change in velocity.
- 📊 Kinematic equations are used to solve for variables in physics problems, often focusing on finding accelerations which are then used in force problems.
- 🎯 In uniformly accelerated motion, the acceleration is constant, which can occur when the net force acting on an object is constant or zero.
- 🌐 Projectile motion involves analyzing the horizontal and vertical components of motion independently, with constant acceleration due to gravity in the vertical direction.
- 📐 When dealing with vectors, it's crucial to use trigonometric relationships (Pythagorean theorem, sine, and cosine) to break down or combine components as needed.
Q & A
What is kinematics in the context of physics?
-Kinematics is the study of the motion of objects without considering the causes of that motion.
What distinguishes a vector from a scalar in physics?
-A vector is a quantity that has both magnitude and direction, while a scalar is a quantity that only has magnitude with no direction associated with it.
How is position represented in physics?
-Position is represented by placing an object on a coordinate system, such as an XY plane, and using its x and y coordinates to determine its location in space.
What is the difference between distance and displacement?
-Distance is the total length of the path traveled by an object, while displacement is the straight-line distance from the initial to the final position, independent of the path taken.
How are speed and velocity related to distance and displacement?
-Speed is the total distance traveled divided by time, measured in meters per second, while velocity is the displacement divided by time and takes direction into account, also measured in meters per second.
What is uniformly accelerated motion and how is it characterized?
-Uniformly accelerated motion occurs when an object's acceleration is constant. This can be due to a constant net force acting on the object or when the net force is zero, resulting in no acceleration.
How does freefall relate to uniformly accelerated motion?
-Freefall is an example of uniformly accelerated motion where an object moves only under the influence of gravity, experiencing a constant acceleration towards the Earth.
What are the key differences in analyzing the horizontal and vertical components of projectile motion?
-In projectile motion, the horizontal component has zero acceleration and constant velocity, while the vertical component has an acceleration of -9.8 m/s^2 due to gravity, causing the velocity to change over time.
How can you calculate the displacement in the Y direction for projectile motion?
-The displacement in the Y direction can be calculated by finding the area under the velocity-time graph for the Y component of the motion, which represents the change in position over time.
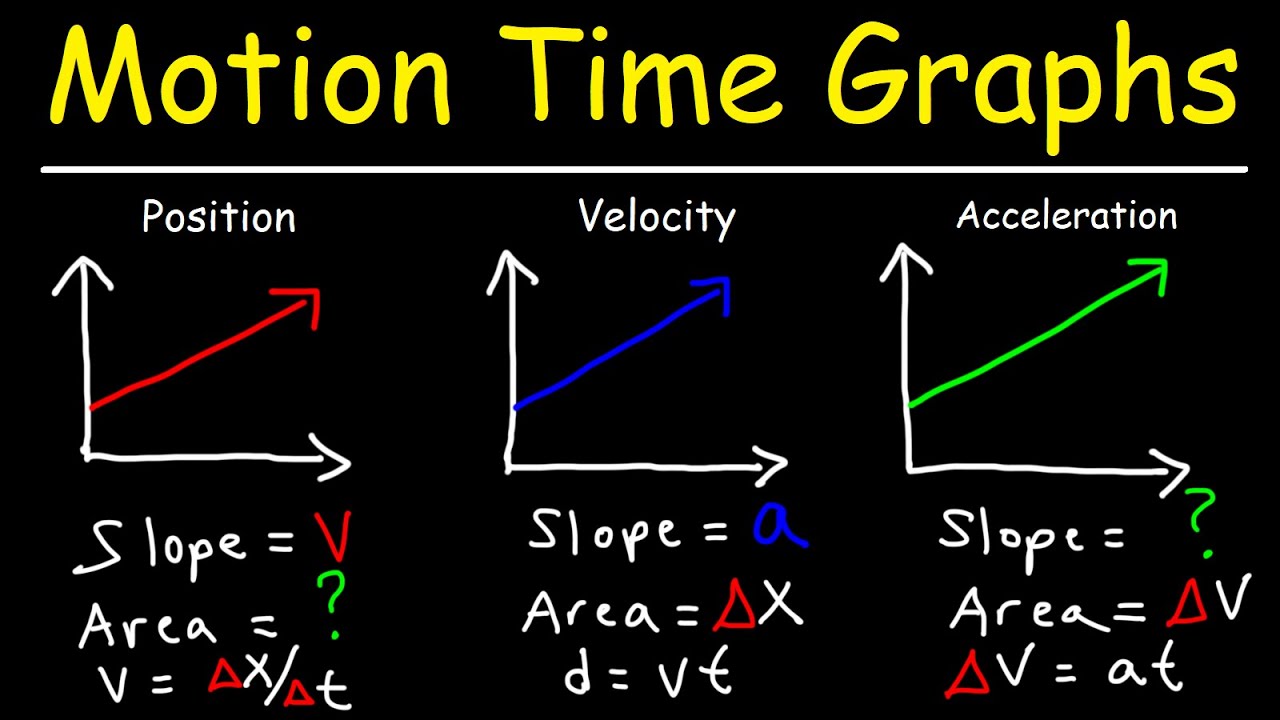
What is the significance of the slope and area under the graphs in analyzing motion?
-The slope of the position-time and velocity-time graphs indicate the velocity and acceleration, respectively. The area under the velocity-time graph represents displacement, while the area under the acceleration-time graph represents the change in velocity.
How can you break down an initial velocity given at an angle into its horizontal and vertical components?
-You can use trigonometric relationships such as the Pythagorean theorem to find the horizontal (VX) and vertical (VY) components, and then apply the concepts of sine and cosine (sohcahtoa) to determine the actual velocities in each direction.
Outlines
📚 Introduction to Kinematics
This paragraph introduces the study of kinematics, focusing on the motion of objects without considering the causes of that motion. It explains the difference between vectors, which have both magnitude and direction, and scalars, which only have magnitude. The concept of position is discussed, emphasizing the use of coordinate systems to track an object's location in space. The distinction between distance, the length of the path traveled, and displacement, the straight-line distance from the initial to the final position, is clarified. The paragraph also highlights the importance of understanding the difference between distance and displacement, as they are not always the same.
📐 Understanding Distance and Displacement
This paragraph delves deeper into the concepts of distance and displacement, emphasizing their differences and how they are measured. It uses a track example to illustrate situations where distance and displacement are not equal. The base unit of length, the meter, is introduced as the standard for measuring both quantities. The paragraph also discusses the scalar nature of distance and the vector nature of displacement, with displacement being represented by an arrow indicating direction. The importance of direction in displacement is stressed, with examples of positive and negative displacements along the x-axis.
🏃♂️ Speed, Velocity, and Acceleration
This paragraph discusses the concepts of speed and velocity, which describe the rate of change in an object's position over time. It differentiates between average speed, which is the total distance traveled divided by time, and average velocity, which is the displacement divided by time. The relationship between distance, displacement, speed, and velocity is further explored. Acceleration is introduced as the change in velocity over time, with examples illustrating how it is calculated. The paragraph also touches on uniformly accelerated motion, where the acceleration is constant, and how it applies to different scenarios.
📊 Kinematic Equations and Freefall
This paragraph presents the kinematic equations, which are used to solve problems involving uniformly accelerated motion. It explains how these equations relate initial and final positions, velocities, acceleration, and time. The concept of instantaneous quantities is introduced, contrasting them with average quantities. The paragraph then applies these concepts to the specific case of freefall, where an object is influenced only by gravity. It provides an example of how to calculate the position and velocity of an object in freefall using the kinematic equations and discusses the linear relationship between velocity and time, as well as the squared relationship between position and time.
🚀 Projectile Motion and Components
This paragraph focuses on projectile motion, where an object is launched at an angle and moves under the influence of gravity. It emphasizes the need to analyze the horizontal and vertical components of the motion independently. The paragraph explains that the horizontal velocity remains constant due to zero acceleration in the horizontal direction, while the vertical velocity changes due to the constant acceleration of gravity. The concept of breaking down a vector into its components using trigonometric relationships is introduced, with the Pythagorean theorem, inverse tangent, sine, and cosine functions being key to understanding these relationships. The paragraph concludes with a reminder of the importance of these concepts in various units of study.
Mindmap
Keywords
💡Kinematics
💡Vector
💡Scalar
💡Position
💡Displacement
💡Distance
💡Speed
💡Velocity
💡Acceleration
💡Uniformly Accelerated Motion
💡Projectile Motion
Highlights
Kinematics is the study of the motion of objects without considering the causes of that motion.
A vector is a quantity that has both magnitude and direction, whereas a scalar only has magnitude.
In physics, the position of an object is tracked using a coordinate system, such as an XY plane.
Distance is the length of the path traveled, while displacement is the straight-line distance from the initial to the final position.
Displacement is a vector and does not depend on the path taken, only on the initial and final positions.
Speed and velocity are related to distance and displacement, respectively, and both describe the rate of change in position.
Average velocity is calculated using the formula (final velocity + initial velocity) / 2.
Acceleration is the rate of change in velocity and is calculated as the change in velocity divided by time.
Uniformly accelerated motion occurs when an object's acceleration is constant, such as in freefall.
In freefall, the object's velocity increases by 9.8 m/s with each second due to the acceleration due to gravity.
Projectile motion involves analyzing the horizontal and vertical components of an object's motion independently.
The horizontal velocity of a projectile is constant because there is no acceleration in the horizontal direction (ignoring air resistance).
The vertical velocity of a projectile changes due to the constant acceleration of gravity (9.8 m/s^2) acting downwards.
The displacement in the Y direction for a projectile launched from and landing at the same height is zero, as the positive and negative displacements cancel out.
The position of a projectile in the X direction increases linearly with time, as the velocity is constant.
The position of a projectile in the Y direction follows a parabolic path, starting from zero, reaching a maximum, and then returning to zero.
The area under the velocity versus time graph represents the displacement, while the area under the acceleration versus time graph represents the change in velocity.
When dealing with projectile motion, it's crucial to consider the initial velocity components in both the horizontal and vertical directions.
The Pythagorean theorem, inverse tangent, and trigonometric functions (SOHCAHTOA) are essential for breaking down and analyzing vector components.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: