Converting between Moles, Atoms, and Molecules (Part 2)

Tyler DeWitt
6 May 201406:58
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script focuses on converting between moles, atoms, and molecules, building upon a previous video. It provides a step-by-step guide for two practice problems: calculating the number of molecules in 0.63 moles and determining the moles of 3.9 x 10^20 magnesium atoms. The script uses the concept of Avogadro's number (6.02 x 10^23) to perform these conversions, illustrating the process with scientific notation and rounding to significant figures. It emphasizes the importance of understanding scientific notation and the practical application of conversion factors in chemistry.

Takeaways
  • 🧪 The concept of a mole is a fundamental unit in chemistry, representing 6.02 x 10^23 entities, whether they are molecules, atoms, or other particles.
  • 📚 The video is a follow-up to a previous one, emphasizing the importance of understanding the first part before proceeding with practice problems.
  • 🔢 To find the number of molecules in a given amount of moles, you multiply the number of moles by Avogadro's number (6.02 x 10^23).
  • 📉 The script explains converting units from moles to molecules using an example with 0.63 moles, illustrating the process step by step.
  • 🧮 The importance of scientific notation is highlighted for handling large numbers, such as 602 hexillion, which is written as 6.02 x 10^23.
  • ✂️ The process of rounding to significant figures is demonstrated, showing how to round a number to two significant figures for simplicity and accuracy.
  • 🔍 The script provides a method to convert moles to molecules using a calculator, emphasizing the use of scientific notation for large numbers.
  • 🔄 The concept of using conversion factors is introduced to solve problems related to moles and molecules, showing how to cancel out units in calculations.
  • 📈 An example problem is solved to demonstrate converting a large number of magnesium atoms (3.9 x 10^20) into moles, using both direct calculation and conversion factors.
  • 📝 The rounding process is again emphasized when converting atoms to moles, rounding the result to two significant figures for clarity.
  • 📖 The script concludes by reiterating the importance of understanding the conversion between moles and the number of atoms or molecules, and how to represent these quantities in scientific notation.
Q & A

  • What is the fundamental principle behind converting between moles, atoms, and molecules?

    -The fundamental principle is that there are always 602 hexillion (6.02 x 10^23) entities in a mole, regardless of whether they are molecules, atoms, jellybeans, or coins. This Avogadro's number is the basis for all conversions.

  • How many molecules are there in 0.63 moles of molecules?

    -To find the number of molecules in 0.63 moles, multiply 0.63 by Avogadro's number, 6.02 x 10^23. The calculation results in 3.7926 x 10^23 molecules, which rounds to 3.8 x 10^23 when considering significant figures.

  • What is the significance of using scientific notation in the script?

    -Scientific notation is used to simplify the representation of very large numbers, such as the number of entities in a mole. It makes calculations and comprehension easier, especially when dealing with significant figures and rounding.

  • How does the script demonstrate converting 0.63 moles of molecules to a number of molecules?

    -The script demonstrates this by multiplying 0.63 moles by 6.02 x 10^23 (Avogadro's number), and then rounding the result to two significant figures to get 3.8 x 10^23 molecules.

  • What is the concept of significant figures and how is it applied in the script?

    -Significant figures are the digits in a number that carry meaningful information about its precision. In the script, after calculating 3.7926 x 10^23 molecules, the number is rounded to 3.8 x 10^23 using significant figures, keeping the first two non-zero digits.

  • Can the number of molecules in moles be represented in a full numerical form with zeros?

    -Yes, the number of molecules in moles can be written out in full with all the zeros. For example, 3.8 x 10^23 can be written as 38,000,000,000,000,000,000,000.

  • What is a conversion factor and how is it used in the script?

    -A conversion factor is a ratio that allows you to convert from one unit to another. In the script, a conversion factor of 1 mole to 6.02 x 10^23 molecules is used to convert moles to the number of molecules.

  • How does the script handle the conversion of 3.9 x 10^20 magnesium atoms to moles?

    -The script divides 3.9 x 10^20 atoms by Avogadro's number, 6.02 x 10^23 atoms per mole, to find the number of moles. The result is then rounded to two significant figures to get 6.5 x 10^-4 moles.

  • Why is it necessary to use scientific notation when dividing large numbers like in the script?

    -Scientific notation is necessary when dividing large numbers to keep the calculations manageable and to avoid errors. It allows for easier computation and interpretation of the results, as seen when dividing 3.9 x 10^20 by 6.02 x 10^23.

  • How does the script illustrate the conversion of atoms to moles using conversion factors?

    -The script uses a conversion factor where 1 mole equals 6.02 x 10^23 atoms. By multiplying the number of atoms by this factor, the atoms cancel out, leaving the result in moles, which is then simplified and rounded.

  • What is the final answer for the number of moles represented by 3.9 x 10^20 magnesium atoms?

    -The final answer, after converting 3.9 x 10^20 magnesium atoms to moles and rounding to two significant figures, is 6.5 x 10^-4 moles.

Outlines
00:00
🧪 Calculating Molecules from Moles

This paragraph explains the concept of converting moles to molecules using the Avogadro's number, which is 6.02 x 10^23. The video demonstrates a practice problem involving 0.63 moles of molecules. It starts by comparing moles to more familiar units like dozens, then multiplies 0.63 by 12 to get an intuitive sense of the number of molecules. Next, it translates the problem into scientific notation, using 6.02 x 10^23 to represent Avogadro's number, and calculates 0.63 times this number to get the total number of molecules. The result is then rounded to two significant figures, resulting in 3.8 x 10^23 molecules. The paragraph also explains how to use conversion factors to solve the problem, emphasizing that the process is the same regardless of the type of particles involved.

05:04
📚 Converting Magnesium Atoms to Moles

The second paragraph focuses on converting the number of atoms to moles, using magnesium atoms as an example. It begins by considering the number of atoms in a dozen and how to calculate the number of moles by dividing the total number of atoms by Avogadro's number. The calculation is presented in scientific notation, dividing 3.9 x 10^20 atoms by 6.02 x 10^23 to find the number of moles. The result is then expressed in scientific notation as 6.478405316 x 10^-4 moles and rounded to two significant figures, yielding 6.5 x 10^-4 moles. The paragraph also illustrates how to use conversion factors to simplify the calculation, emphasizing the importance of understanding scientific notation and significant figures in chemistry.

Mindmap
Keywords
💡moles
Moles are a fundamental unit in chemistry used to express amounts of a chemical substance. Defined as the number of elementary entities (such as atoms, molecules, ions, or electrons) in one mole, which is equal to Avogadro's number, approximately 6.02 x 10^23. In the video, moles are the central theme for converting between different quantities of substances, such as molecules and atoms, as seen when calculating the number of molecules in 0.63 moles.
💡atoms
Atoms are the basic units of matter and the defining structure of elements. They consist of protons, neutrons, and electrons. The video discusses converting between moles and atoms, illustrating this with an example of determining how many moles are present in 3.9 x 10^20 magnesium atoms.
💡molecules
Molecules are groups of two or more atoms bonded together, representing the smallest fundamental unit of a chemical compound that can take part in a chemical reaction. The script uses molecules to demonstrate calculations involving moles, such as finding out how many molecules are in 0.63 moles of molecules.
💡Avogadro's number
Avogadro's number is the term used to describe the constant number of particles (usually 6.02 x 10^23) contained in one mole of a substance. It is essential for understanding the relationship between moles and the actual number of particles, as highlighted when converting moles to molecules or atoms in the video.
💡scientific notation
Scientific notation is a way of expressing very large or very small numbers in a compact form using powers of ten. In the script, scientific notation is used to handle the large numbers involved in mole calculations, such as expressing Avogadro's number as 6.02 x 10^23.
💡significant figures
Significant figures are the digits in a number that carry meaningful information about its precision. The video emphasizes the importance of rounding to the correct number of significant figures when presenting scientific results, exemplified when rounding the result of 0.63 moles of molecules to 3.8 x 10^23.
💡conversion factors
Conversion factors are used in calculations to change the units of a physical quantity. In the video, conversion factors are used to transform the number of moles into the number of molecules or atoms, and vice versa, as shown in the step-by-step calculations provided.
💡dozens
A dozen is a simple unit of count used to represent twelve items. In the script, dozens are used as an analogy to help understand the concept of moles, by comparing the process of converting moles to dozens to emphasize the multiplication involved.
💡hexillion
Hexillion is a number that represents a 1 followed by 24 zeros, or 10^24. The video uses the term '602 hexillion' to describe the large number of entities in a mole, making the abstract concept of Avogadro's number more tangible.
💡calculator
A calculator is an electronic device used to perform arithmetic operations and calculations. The script mentions using a calculator to perform the multiplication and division necessary for mole conversions, such as calculating 0.63 times Avogadro's number.
💡rounding
Rounding is the process of adjusting a number to a certain number of significant figures or to a standard form. The video explains how to round numbers in scientific notation to maintain accuracy and simplicity, as shown when rounding 3.7926 x 10^23 to 3.8 x 10^23.
Highlights

Introduction to the second part of a chemistry tutorial on converting between moles, atoms, and molecules.

Explanation that the number of entities in a mole is constant, regardless of the type of molecules or atoms.

Illustration using the analogy of dozens to explain the concept of moles.

Conversion of 0.63 moles of molecules into a numerical value using Avogadro's number.

Use of scientific notation to express Avogadro's number as 6.02 x 10^23.

Calculation of molecules in 0.63 moles using multiplication and scientific notation.

Rounding the result to two significant figures to obtain 3.8 x 10^23 molecules.

Emphasis on the practicality of scientific notation as a shorthand for large numbers.

Introduction of conversion factors for solving chemistry problems involving moles.

Demonstration of converting moles to molecules using a conversion factor.

Explanation of how to cancel out units in a conversion factor to simplify calculations.

Conversion of 3.9 x 10^20 magnesium atoms into moles using Avogadro's number.

Use of scientific notation for the calculation and conversion of atoms to moles.

Rounding the result to two significant figures to get 6.5 x 10^-4 moles.

Clarification that scientific notation is not a 'Martian number' but a way to handle large or small values.

Final conversion of the result from scientific notation to a standard decimal form.

Summary of the process for converting between moles and the number of atoms or molecules.

Transcripts

Browse More Related Video

Converting Between Moles, Atoms, and Molecules

02 - What is Avogadro's Number & the Mole in Chemistry? Part 1

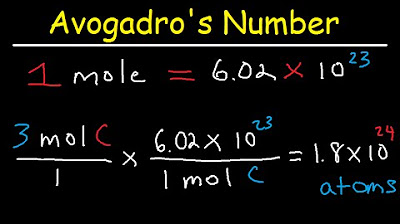
Avogadro's Number, The Mole, Grams, Atoms, Molar Mass Calculations - Introduction

How to Convert Units in Chemistry

How many molecules are in 76.3 g of N2O4 ?

How many atoms of Aluminum are in 0.250 grams of aluminum?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Chemistry BasicsMole ConversionMolecular ScienceEducational ContentScientific NotationPractice ProblemsChemistry TutorialMole to AtomConcept ExplanationLearning Resource