Lec 31 | MIT 18.01 Single Variable Calculus, Fall 2007
TLDRThis MIT OpenCourseWare lecture delves into the geometric concepts of arc length and surface area, foundational for multivariable calculus. The professor explains the arc length formula, \( \sqrt{1 + (dy/dx)^2} \), using examples including linear functions and curves like a semicircle and a parabola. The lecture progresses to surface area calculations, particularly for solids of revolution, such as a sphere and a paraboloid. The material builds towards understanding parametric equations and their application to describe curves and trajectories in a multivariable context, preparing students for advanced calculus topics.
Takeaways
- 📚 The lecture introduces the concept of arc length and its significance in multivariable calculus, emphasizing the transition from integral formulas to geometric applications.
- 🛣️ The arc length (s) of a curve is described as the total distance along the curve, parameterized by s, which can be visualized with points and straight lines approximating the curve as the intervals become smaller.
- 📏 The formula for arc length is derived from the Pythagorean theorem, using the infinitesimal changes in x (dx) and y (dy), represented as √(dx^2 + dy^2).
- 📝 The professor clarifies the notation for arc length, emphasizing that ds is a single entity, not d times s, and should be understood as an infinitesimal segment of the curve.
- 🔍 Different forms of the arc length formula are presented, including the factored form √(1 + (dy/dx)^2) and the Newtonian notation √(1 + f'(x)^2), with y = f(x).
- 📉 The lecture demonstrates the calculation of arc length for linear functions and emphasizes the broader applicability of calculus to determine arc lengths for any curve.
- 🔴 The geometric interpretation of radians and the sine function is explored through the arc length of a circle, providing a foundational understanding of these trigonometric concepts.
- 📐 The calculation of the arc length of a parabola y = x^2 is discussed, with an example of how to set up the integral for its solution, although the actual integration is not carried out in detail.
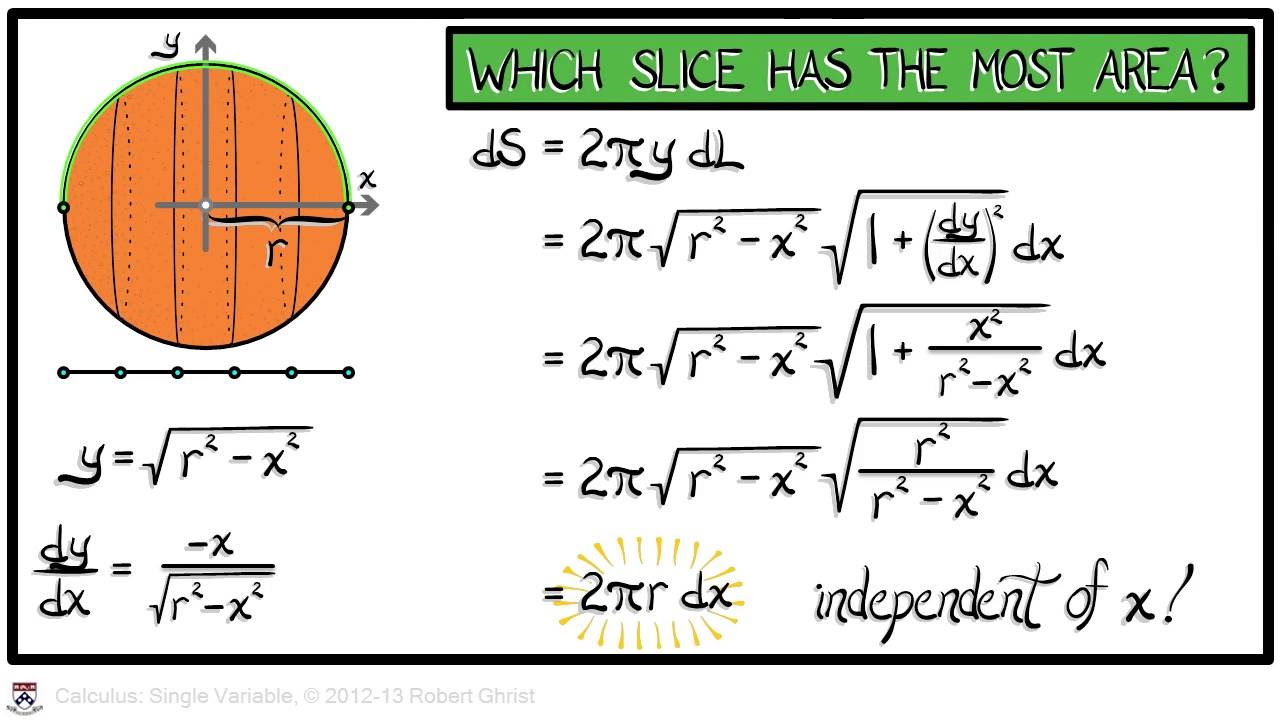
- 🌀 The concept of surface area in three-dimensional space is introduced, with an example of the surface area of a sphere obtained by rotating a curve around an axis.
- 📈 The method for calculating the surface area of a sphere using parametric equations and integration is outlined, leading to a simple formula for the total surface area.
- 🔄 The lecture concludes with an introduction to parametric equations and curves, setting the stage for further exploration in multivariable calculus and different coordinate systems.
Q & A
What is the main topic discussed in the script?
-The main topic discussed in the script is the concept of arc length in the context of calculus, which serves as an introduction to tools used in multivariable calculus.
What is the formula for calculating arc length?
-The formula for calculating arc length is the integral from a to b of the square root of 1 + (dy/dx)^2 dx, where 'a' and 'b' are the limits of integration and dy/dx is the derivative of y with respect to x.
Why is it important to understand arc length in calculus?
-Understanding arc length is important in calculus because it provides the foundation for calculating distances along curved paths, which is essential for studying multivariable calculus and analyzing more complex geometric and physical phenomena.
What is the significance of the parameter 's' in the context of arc length?
-In the context of arc length, the parameter 's' represents the arc length itself, which is a measure of the distance along a curve. It is used to approximate the length of a curve by dividing it into small straight segments.
Can you provide an example of how arc length is calculated for a linear function?
-For a linear function like y = mx, the arc length from x = 0 to x = 10 would be the integral from 0 to 10 of the square root of 1 + m^2 dx, which simplifies to 10 times the square root of 1 + m^2, as 'm' is the slope of the line.
What is the geometric interpretation of the arc length formula when applied to a circle?
-When applied to a circle, the arc length formula provides a direct relationship between the length of an arc and the angle it subtends at the center of the circle, leading to a correct definition of radians and trigonometric functions like sine.
How does the script relate the concept of arc length to the definition of sine and radians?
-The script demonstrates that the arc length along a circle can be used to define radians and the sine function. Specifically, if the arc length is 'alpha' and the radius is 1, then sine alpha equals the horizontal distance 'a', providing a geometric interpretation of the sine function.
What is the connection between the arc length formula and the surface area of a sphere?
-The arc length formula is used as a basis to derive the formula for the surface area of a sphere when considering a sphere sliced into infinitesimal rings and integrating the circumferences of these rings over the sphere's height.
Can you explain the concept of parametric equations mentioned in the script?
-Parametric equations are a way to describe a curve in which both x and y are expressed as functions of a third variable, called the parameter, often denoted by 't'. This allows for the representation of more complex curves and trajectories in a coordinate plane.
What is the trajectory described by the parametric equations x = a cos t and y = a sin t?
-The trajectory described by the parametric equations x = a cos t and y = a sin t is a circle with radius 'a'. The parameter 't' represents the angle in radians, and as 't' varies from 0 to 2π, the point (x, y) traces out the circle in a counterclockwise direction.
Outlines
📚 Introduction to Arc Length and Geometry
The professor begins by discussing the transition from integral formulas to geometry, which serves as a foundation for multivariable calculus. The primary focus is on the concept of arc length, which is introduced through the analogy of a roadway with mileage markers. The arc length, denoted by 's', is explained as the length along the road. The approximation of arc length is likened to connecting points on the curve with straight lines, which becomes increasingly accurate as the divisions become smaller. The formula for calculating the arc length increment, 'delta s', is derived from the Pythagorean theorem, relating the horizontal and vertical distances between points on the curve. The infinitesimal approach of calculus is emphasized, leading to the formula for arc length, which involves the square root of the sum of the squares of differentials of x and y (dx and dy). The professor also clarifies common notational conventions, such as the use of 'ds' to represent the differential of 's', not the product of 'd' and 's'.
📐 Deriving Arc Length Formulas and Their Variants
The professor elaborates on the formula for arc length, presenting it in multiple forms to emphasize its versatility. The primary form involves the square root of '1 + (dy/dx)^2 dx', which is derived from the basic differential form. Variants of this formula are introduced, such as factoring out 'dx' to yield '1 + (dy/dx)^2', which is particularly useful for practical applications. The professor also addresses common notational shorthand, such as 'integral ds', which is used informally in many textbooks. Additionally, the professor clarifies misconceptions, such as the incorrect assumption that 'f''(x) = (f'(x))^2', by providing a counterexample. The importance of understanding the limits of integration in relation to the variable 's' used for arc length is also discussed, distinguishing 's0' and 'sn' as mileage markers along the curve, as opposed to 'a' and 'b' which are points on the x-axis.
📏 Calculating Arc Length of Linear and Curved Functions
The professor provides examples to illustrate the calculation of arc length. The first example involves a linear function, 'y = mx', where the arc length is calculated from 0 to 10, resulting in a straightforward application of the Pythagorean theorem. This example serves to demonstrate that while simple, the principles of calculus enable the calculation of arc length for any function, not just linear ones. The second example involves a semicircle defined by 'y = sqrt(1 - x^2)', where the derivative 'y'' is calculated to find the arc length element 'ds'. The integral for the arc length of the semicircle is set up, leading to a more complex calculation that highlights the application of calculus to curved functions.
🔶 Geometric Interpretation of Arc Length and Radians
The professor delves into the geometric interpretation of arc length, using the example of a circle to establish a connection between arc length and radians. By calculating the arc length of a semicircle, the professor derives the relationship between the angle in radians and the arc length, showing that 'sin(alpha) = a', where 'alpha' is the angle in radians and 'a' is the horizontal distance along the circle's arc. This leads to a foundational definition of radians and the sine function, emphasizing that the sine of an angle is defined by the ratio of the opposite side to the hypotenuse in a right-angled triangle. The professor highlights the significance of this approach in providing a rigorous definition of trigonometric functions based on first principles.
🌐 Transitioning to Three-Dimensional Space: Surface Area
The professor transitions from two-dimensional arc length to three-dimensional surface area, introducing the concept as a natural extension of the principles learned in multivariable calculus. The focus is on the surface area of rotation, using the previously discussed parabola 'y = x^2' as an example. The surface area is visualized as the outer 'skin' of a three-dimensional shape formed by rotating the parabola around the x-axis. The formula for surface area involves the circumference of the circles formed at each point of rotation, multiplied by the arc length of the curve. The professor emphasizes the importance of understanding the simplest cases, such as linear functions, as a foundation for tackling more complex problems in three-dimensional space.
🎯 Calculating Surface Area of a Sphere and a Paraboloid
The professor discusses the calculation of surface area for a sphere and a paraboloid. For the sphere, the formula for surface area is derived by considering a small section of the sphere's surface and integrating over the entire surface. The result is a simple formula involving the radius of the sphere, '2 pi a^2', which is verified by considering special cases like a hemisphere and the entire sphere. The professor also revisits the paraboloid example, setting up the integral for surface area by considering the rotation of the parabola 'y = x^2' around the x-axis. The integral involves the square root of '1 + 4x^2', which was previously derived for arc length, and emphasizes the method and setup of the integral rather than the computation itself.
🛤️ Parametric Equations and Curves in Multivariable Calculus
The professor concludes the lecture by introducing parametric equations and their significance in multivariable calculus. Parametric equations are presented as a way to describe curves where 'x' and 'y' are both functions of a parameter 't', which can be thought of as time. The professor uses the example of a circle defined by 'x = a cos t' and 'y = a sin t' to illustrate how parametric equations can reveal the shape of a curve and its trajectory over time. By squaring and adding the parametric equations, the professor demonstrates that the curve is a circle with radius 'a'. The direction of the trajectory on the circle is also discussed, indicating that the curve is traversed counterclockwise. The lecture ends with a preview of the next topic: arc length in the context of parametric equations.
Mindmap
Keywords
💡Arc Length
💡Riemann Sums
💡Infinitesimal
💡Hypotenuse
💡Differentiation
💡Integral
💡Surface Area
💡Parametric Equations
💡Trajectory
💡Polar Coordinates
Highlights
Introduction to arc length as a fundamental concept leading into multivariable calculus.
Explanation of arc length using the parameter s and its approximation through straight lines.
Derivation of the arc length formula using the limit of infinitesimally small segments.
Clarification of the notation ds for arc length differential, emphasizing it is not d * s but a single entity.
Presentation of the arc length formula in various forms, including the square root of dx^2 + dy^2.
Discussion on the difference between f'(x)^2 and f''(x), with a specific example using f(x) = x^2.
Illustration of how to calculate arc length for linear functions and the significance for calculus.
Introduction of the circle's arc length calculation with the function y = sqrt(1 - x^2).
Demonstration of the geometric interpretation of radians and sine through arc length.
Foundational approach to defining radians and sine functions based on arc length.
Calculation of the arc length of a parabola y = x^2 using integration techniques.
Introduction to surface area in three-dimensional space and its importance in multivariable calculus.
Explanation of the surface area of rotation, using the parabola y = x^2 as an example.
Derivation of the surface area formula for a sphere and its simplification to 2 pi a(x2 - x1).
Verification of the surface area formula through special cases like hemisphere and whole sphere.
Discussion on rotating around the y-axis and the equivalence of results using dx or dy.
Introduction to parametric equations and their role in describing curves in multivariable calculus.
Example of a parametric circle given by x = a cos t and y = a sin t, and its trajectory analysis.
Concept of trajectory and how it represents the movement on a curve over time.
The transition to multivariable thinking through parametric equations and polar coordinates.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: