Lesson 12 - Surface Area Of Revolution In Parametric Equations

Math and Science
18 Aug 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThis advanced calculus tutorial focuses on calculating the surface area of revolution for parametric equations. Building on previous lessons about arc length and surface area in Cartesian coordinates, the instructor introduces the concept in a parametric context. The formula for surface area is presented as an integral involving \(2\pi y(t)\) times the square root of \((dx/dt)^2 + (dy/dt)^2\), integrated over the parameter \( t \). The tutorial explains how this formula is analogous to the Cartesian version, with \( y(t) \) representing the function's value and the derivatives determining the arc length and circumference of the cross-sectional slice. The lesson aims to simplify the understanding of a complex topic by drawing parallels with familiar concepts.

Takeaways
  • 📚 The lesson covers the topic of surface area of revolution in parametric equations, a natural progression from previous topics.
  • 🔍 The instructor reviews previous topics, including regular functions, arc length, and surface area of a function rotated about the x-axis in Cartesian coordinates.
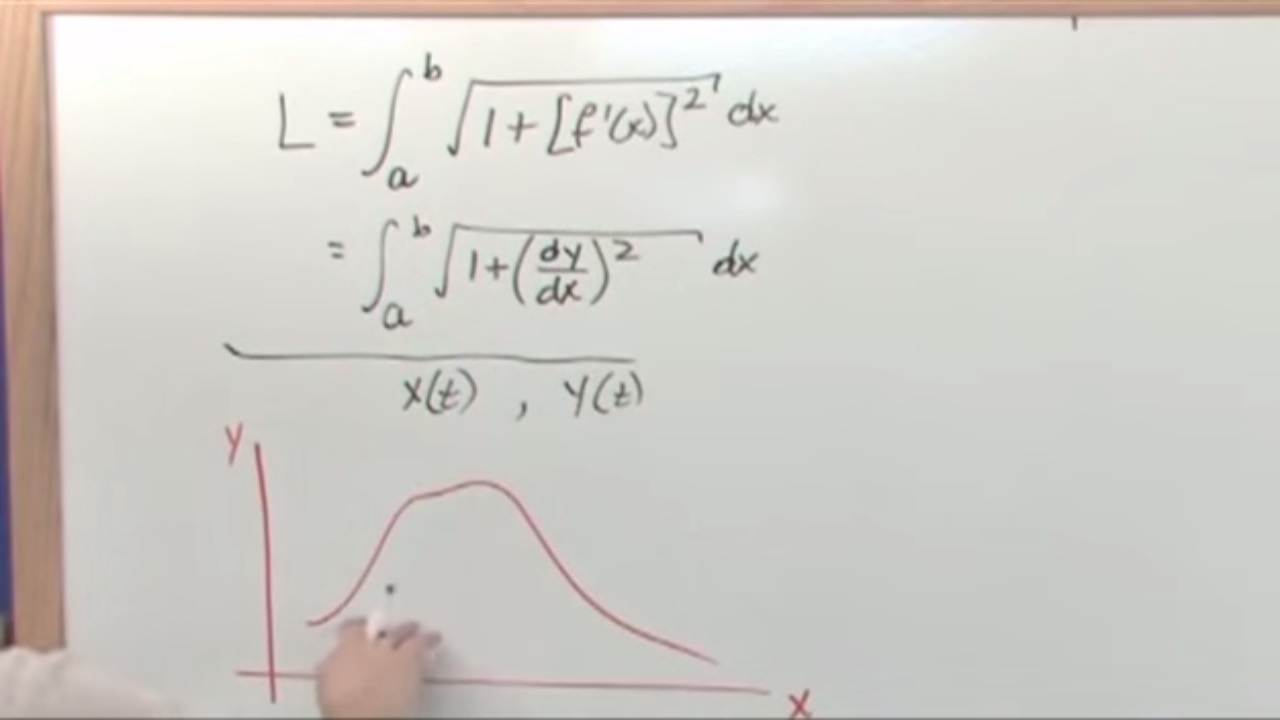
  • 📈 Parametric equations are introduced as functions of (T), where (X = X(T)) and (Y = Y(T)), differing from traditional functions (f(x)).
  • 📐 The arc length in parametric equations is discussed, which is derived similarly to the Cartesian version.
  • 🌀 The surface area of revolution is defined as the integral from (A) to (B) of (2π f(x) √(1 + (f'(x))^2) dx) for Cartesian functions.
  • 📊 The formula for the surface area of revolution in parametric equations is given without proof, but is expected to be intuitively understood by analogy.
  • 🧩 The parametric version of the surface area formula involves integrating (2π Y(T) √((dX/dT)^2 + (dY/dT)^2) dT) from (α) to (β).
  • 🔗 The formula's components are connected to previously discussed concepts, such as the circumference of a slice and the arc length.
  • 📝 The circumference of a slice in parametric equations is analogous to the Cartesian version, using the derivatives with respect to (T).
  • 📚 The lesson aims to help students understand the transition from Cartesian to parametric equations in the context of calculating surface areas of revolution.
  • 🔑 The key to the lesson is recognizing the similarities between the Cartesian and parametric forms of the formulas and understanding how to apply them.
Q & A

  • What is the main topic of this tutorial section?

    -The main topic of this tutorial section is the calculation of the surface area of revolution in parametric equations.

  • What is the significance of the term 'parametric equations' in this context?

    -Parametric equations are used to describe the coordinates of a point as functions of a third variable, called the parameter. In this context, they are used to define the surface area of revolution when the functions are rotated around an axis.

  • What is the formula for the surface area of revolution in Cartesian coordinates?

    -The formula for the surface area of revolution in Cartesian coordinates is 2 * pi * f(x) * sqrt(1 + (f'(x))^2) dx, integrated from A to B.

  • What does 'f of X' represent in the context of the surface area of revolution?

    -'f of X' represents the function that is being rotated around the x-axis to create the surface of revolution.

  • What is the circumference of a slice in the context of surface area of revolution?

    -The circumference of a slice refers to the perimeter of the circular cross-section created when the function is rotated around the x-axis at a particular value of x.

  • How is the arc length of a curve related to the surface area of revolution?

    -The arc length of a curve is a component used to calculate the surface area of revolution. It represents the length of the curve that forms the circumference of a slice when the function is rotated.

  • What is the integral that represents the surface area of revolution in parametric equations?

    -The integral representing the surface area of revolution in parametric equations is 2 * pi * y(t) * sqrt((dx/dt)^2 + (dy/dt)^2) dt, integrated from alpha to bravo.

  • What is the role of 'y of T' in the parametric equation for surface area of revolution?

    -'y of T' represents the y-coordinate as a function of the parameter T, and it is used to calculate the circumference of a slice in the parametric version of the surface area of revolution.

  • What is the significance of the square root term in the parametric integral?

    -The square root term, sqrt((dx/dt)^2 + (dy/dt)^2), represents the derivative of the parametric curve, which is analogous to the derivative in the Cartesian version and is used to calculate the circumference of a slice.

  • How does the tutorial suggest that the parametric version of the surface area of revolution is derived?

    -The tutorial suggests that the parametric version is derived by analogy to the Cartesian version, using the length of the curve from the previous section on parametric equations and the circumference of a slice.

  • What is the purpose of integrating the formula for surface area of revolution?

    -The purpose of integrating the formula is to sum up the infinitesimal contributions of the circumference of each cross-sectional slice along the entire length of the curve, which gives the total surface area of the revolution.

Outlines
00:00
📚 Introduction to Surface Area of Revolution in Parametric Equations

This paragraph introduces the topic of surface area of revolution in parametric equations, a natural progression from previous lessons on advanced calculus. The instructor reviews the concepts covered so far, including regular functions, Cartesian functions, arc length, and surface area of functions rotated around the x-axis in Cartesian coordinates. The focus then shifts to parametric equations, which are functions defined by X(T) and Y(T) rather than f(x), and the arc length in parametric equations. The instructor promises a simple analogy to derive the equation for surface area of revolution in parametric equations, which will be discussed in detail in the subsequent sections.

Mindmap
Keywords
💡Surface Area of Revolution
The term 'Surface Area of Revolution' refers to the total surface area of an object that is formed by revolving a planar curve around an axis. In the context of the video, this concept is central to understanding how to calculate the surface area of a shape created when a parametric curve is rotated around an axis. The script mentions that the surface area of revolution in Cartesian coordinates is given by the integral of 2πf(x)√(1+(f'(x))²)dx, which is a fundamental formula discussed and used to derive the parametric version.
💡Parametric Equations
Parametric equations are a way of defining a curve in a plane where the coordinates of the points on the curve are expressed as functions of a third variable, called the parameter. In the video, parametric equations are introduced as X(t) and Y(t), as opposed to the traditional y = f(x) form. They are essential for understanding how to calculate arc length and surface area of revolution when dealing with curves that are not easily described by a single function of x.
💡Arc Length
Arc length is the measure of the distance along a curve between two points. In the video, the concept of arc length is discussed in relation to both Cartesian functions and parametric equations. The script mentions that the arc length for parametric equations is derived similarly to the Cartesian version, emphasizing the connection between the two approaches.
💡Parameter
In parametric equations, the 'parameter' is a variable, often denoted by t, that is used to define the coordinates of points on a curve. The script explains that instead of having a function f(x), parametric equations use X(t) and Y(t), where t is the parameter that varies to trace out the curve.
💡Integration
Integration is a fundamental concept in calculus that involves finding the accumulated value of a function over an interval. In the video, integration is used to calculate both the arc length and the surface area of revolution. The script mentions integrating over x for Cartesian functions and over t for parametric equations to find the respective quantities.
💡Circumference
Circumference refers to the total length of the edge of a circle or ellipse. In the context of the video, the circumference is used to describe the edge of a cross-sectional slice of the surface of revolution. The script explains that the circumference of a slice when revolving a parametric curve is given by 2πy, where y is the function of the parameter t.
💡Cross-Sectional Slice
A 'cross-sectional slice' is a virtual cut made through an object to reveal its internal structure or shape. In the video, the concept is used to describe the circular or elliptical shape created when a curve is rotated around an axis. The script illustrates that the circumference of this slice is a key component in calculating the surface area of revolution.
💡Derivatives
Derivatives in calculus represent the rate at which a function changes with respect to its variable. In the video, derivatives are used to find the rate of change of X(t) and Y(t) with respect to t, which is essential for calculating the arc length and the circumference of a slice in parametric equations.
💡Square Root
The square root operation is used to find a value that, when multiplied by itself, gives the original number. In the video, the square root is used in the formula for the surface area of revolution to account for the curvature of the cross-sectional slice. The script mentions the square root of (dX/dt)² + (dY/dt)² as part of the integral for the parametric version.
💡Cartesian Coordinates
Cartesian coordinates are a two-dimensional coordinate system where each point is defined by an ordered pair of numbers, typically (x, y). The video script contrasts Cartesian coordinates with parametric equations, explaining that while Cartesian coordinates use y = f(x), parametric equations involve functions of a parameter t.
Highlights

Introduction to the topic of surface area of revolution in parametric equations.

Natural progression from previous topics including regular functions, arc length, and surface area of revolution in Cartesian coordinates.

Explanation of parametric equations as functions with parameters T instead of f(X).

Review of arc length in parametric equations derived similarly to Cartesian functions.

Introduction of the formula for surface area of revolution in Cartesian coordinates: 2π * f(X) * √(1 + (f'(X))^2).

Description of the circumference of a slice in the context of surface area of revolution.

Visual representation of a function and its cross-sectional slice when rotated around an axis.

Integration over X to calculate the surface area of revolution in Cartesian coordinates.

Transition to the corresponding formula for surface area of revolution in parametric equations.

Presentation of the parametric equation formula: 2π * y(T) * √((dx/dt)^2 + (dy/dt)^2) integrated over T.

Comparison of the parametric equation formula to the Cartesian version, emphasizing the similarity.

Explanation of the circumference of a slice in parametric equations as analogous to the Cartesian version.

Derivation of the arc length in parametric equations from the previous section.

Emphasis on the simplicity and ease of use of the parametric equation formula for surface area of revolution.

Illustration of the parametric version of coordinates and the function X(T).

Transcripts

Browse More Related Video

Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

Lec 31 | MIT 18.01 Single Variable Calculus, Fall 2007

AP Calculus BC Lesson 9.1

Introduction to the line integral | Multivariable Calculus | Khan Academy

Line integral example 1 | Line integrals and Green's theorem | Multivariable Calculus | Khan Academy

Related rates of volume and area of a cube

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Advanced CalculusSurface AreaRevolutionParametricEquationsArc LengthIntegrationCartesianTutorialsEducation