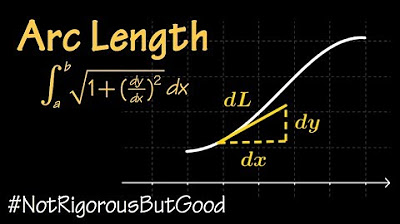Unit IV: Lec 4 | MIT Calculus Revisited: Single Variable Calculus
TLDRThis MIT OpenCourseWare lecture explores the concept of 'one-dimensional area', focusing on arc length. It contrasts the complexities of measuring length with those of area and volume, highlighting the unique challenges in calculating arc length. The professor introduces axioms for arc length, discusses the limitations of intuitive approaches, and delves into analytical methods using calculus. The lecture also addresses the Mean Value Theorem and the first fundamental theorem of integral calculus to provide a rigorous definition of arc length, emphasizing the importance of higher-order infinitesimals in ensuring the accuracy of approximations.
Takeaways
- 📚 The lecture introduces the concept of 'One-dimensional Area', which is actually the study of arc length, contrasting it with the seemingly simpler concepts of area and volume.
- 📐 The fundamental axioms for arc length are presented, starting with the assumption that the length of any straight line segment can be measured and that the total length of an arc is the sum of its parts.
- 🔍 A key difference between arc length and other measures of length is highlighted: the perimeter of a region does not necessarily follow the containment principle of being less than or equal to the perimeter of a containing region.
- 📉 The lecture delves into the analytical approach to length, emphasizing the need for an objective method that aligns with our intuitive understanding of arc length, as opposed to the traditional string method.
- ❌ The first analytical approach, which involved approximating arc length by the difference in x-values (delta x), is shown to be inadequate and not reflective of the true arc length.
- 📈 An alternative approach is introduced, where arc length is approximated by the cord joining the endpoints of the arc, leading to the definition of arc length as a limit involving the sum of these cord lengths.
- 🧩 The Mean Value Theorem is applied to show that for smooth curves, the slope of the cord approximates the derivative of the function at some point within the interval, allowing for the use of calculus in computing arc length.
- 💡 The first fundamental theorem of integral calculus is invoked to express the arc length in terms of a definite integral, provided that the derivative of the function is continuous.
- 🤔 The lecture poses critical questions about the existence of the limit defining arc length, how to compute it, and most importantly, how to ensure that this limit corresponds with the intuitive definition of arc length.
- 📝 The process of justifying the approximation of arc length by straight line segments is discussed, involving the concept of higher order infinitesimals and the careful 'squeezing' of errors in the approximation.
- 🌟 The conclusion of the lecture affirms the validity of the intuitive approach to approximating arc length by straight line segments, after a rigorous analytical justification.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the study of length, specifically focusing on the concept of arc length and its relationship to calculus.
Why does the professor refer to the study of arc length as 'one-dimensional area'?
-The professor refers to arc length as 'one-dimensional area' because it is a concept that extends the idea of area and volume to a single dimension, similar to how area is two-dimensional and volume is three-dimensional.
What are the two axioms discussed in the lecture for measuring arc length?
-The two axioms discussed are: 1) The basic building block for measuring arc length is a straight line segment, and 2) The length of the whole equals the sum of the lengths of the parts.
Why is it incorrect to assume that if region 'R' is contained in region 'S', then the perimeter of 'R' is less than or equal to the perimeter of 'S'?
-It is incorrect because, unlike area and volume, the concept of arc length does not adhere to the principle that a smaller region has a smaller perimeter. Complex shapes can have a greater perimeter than simpler shapes that contain them.
What is the intuitive approach to measuring arc length mentioned in the lecture?
-The intuitive approach to measuring arc length is to use a piece of string, lay it along the curve from point A to point B, pick it up, straighten it out, and then measure its length with a ruler.
What is the first analytical approach to arc length that the professor discusses?
-The first analytical approach discussed is to approximate the arc length by using the length of the x-axis interval (delta x) as an approximation for the arc length (delta w) and then taking the limit of the sum of these approximations as the number of divisions approaches infinity.
Why does the first analytical approach fail to provide an accurate measure of arc length?
-The first analytical approach fails because it does not account for the curvature of the arc. It simply sums up the lengths of the x-axis intervals, which does not reflect the actual path length of the curve.
What is the second analytical approach to measuring arc length presented in the lecture?
-The second analytical approach involves approximating the arc length (delta w) by the length of the cord joining the endpoints of the arc (delta s), and then taking the limit of the sum of these approximations as the number of divisions approaches infinity.
How does the lecture relate the concept of arc length to the Mean Value Theorem?
-The lecture uses the Mean Value Theorem to show that for a smooth curve, there exists a point within the interval where the slope of the curve is equal to the slope of the cord, which helps in approximating the arc length more accurately.
What is the fundamental theorem of integral calculus used to justify the second analytical approach?
-The first fundamental theorem of integral calculus is used to justify that if the derivative (which represents the slope of the curve) is continuous, then the arc length can be computed as the definite integral of the square root of '1 + (dy/dx)^2' with respect to x from 'a' to 'b'.
What is the main challenge in proving that the second analytical approach accurately measures arc length?
-The main challenge is to show that the limit of the sum of the approximations (using delta s) as the number of divisions approaches infinity is equal to the actual arc length, and that all the error has been squeezed out in the limit.
How does the lecture conclude the justification for using straight line segments to approximate arc length?
-The lecture concludes by showing that the error in approximating arc length with straight line segments is a higher order infinitesimal, which means it approaches zero faster than the length of the segment itself, thus justifying the intuitive approach.
Outlines
📚 Introduction to 'One-dimensional Area' and Arc Length
This paragraph introduces the concept of 'One-dimensional Area', which is actually the study of arc length. The professor begins by discussing the complexities of measuring length in calculus, which differs from area and volume due to the peculiarities of arc length. The traditional building blocks for area and volume are rectangles and cylinders, respectively, but for arc length, the basic unit is a straight line segment. The professor emphasizes two axioms: the measurable length of any straight line segment and the additive property of lengths. However, a third axiom, which was applicable to area and volume, does not hold for arc length, leading to a conceptual challenge in understanding the perimeters of contained regions.
🔍 Analytical Approach to Arc Length and the Limit of 'Delta x'
The second paragraph delves into an analytical approach to defining arc length, starting with the intuitive method of using a string to measure the length of a curve. The professor then explores the idea of approximating arc length by using the length of the line segment ('delta x') between points on the curve. This leads to a definition of arc length as the limit of the sum of 'delta x's as the number of divisions ('n') approaches infinity. However, this method results in the linear distance between two endpoints rather than the actual arc length, indicating a need for a more sophisticated approach.
📐 Refining the Arc Length Approximation with 'Delta S'
In this paragraph, the professor introduces a refined method for approximating arc length using 'delta s', which represents the cord between endpoints of an arc segment, as opposed to 'delta x'. This approach is based on the Pythagorean theorem, where 'delta s' is the hypotenuse of a right triangle with sides 'delta x' and 'delta y'. The professor defines the arc length 'L' from 'a' to 'b' as the limit of the sum of 'delta s's as 'n' approaches infinity. This leads to a discussion of three critical questions: whether the limit exists, how to compute it, and how to ensure it aligns with the intuitive definition of arc length.
🧩 The Mean Value Theorem and Its Application to Arc Length
The fourth paragraph discusses the application of the Mean Value Theorem (MVT) to arc length. The MVT is used to establish that for a smooth curve, there exists a point within each interval where the slope of the curve equals the slope of the cord. This allows the professor to express the arc length 'L' from 'a' to 'b' as a definite integral involving the derivative of the function 'f', which represents the curve. The conditions under which this integral accurately represents arc length are explored, including the requirement for the derivative to be continuous.
🤔 The Challenge of Proving Arc Length Equals the Integral
This paragraph addresses the third question raised earlier: proving that the limit of the sum of 'delta s's is indeed equal to the actual arc length 'w'. The professor discusses the difficulties in demonstrating that all approximation errors have been eliminated, likening the challenge to the sensitivity of the 0/0 indeterminate form in differential calculus. The paragraph sets the stage for a general discussion on how to prove that a given limit equals a function 'w' when approximated by an intuitive function 'g'.
🔧 Generalizing the Proof of Integral Equality to Functions
The professor generalizes the problem of proving that a limit equals a function 'w', which is approximated by an intuitive function 'g'. The discussion involves breaking down 'w' into increments 'delta w' and approximating these increments with a product of 'g' and 'delta x', plus a correction factor. The key is to show that the error term is a higher-order infinitesimal, ensuring that as 'delta x' approaches zero, the error is squeezed out. The paragraph explores different cases of 'alpha sub k' to illustrate when the limit of the sum of the errors will be zero, thus proving the equality.
📉 The Sensitivity of Infinitesimals in Integral Calculus
In this paragraph, the professor emphasizes the sensitivity of using infinitesimals in integral calculus, particularly the 'infinity times 0' indeterminate form. The discussion includes a hypothetical case where 'alpha sub k' is a constant, leading to a non-zero limit and thus an incorrect approximation of 'w'. In contrast, if 'alpha sub k' is a constant times 'delta x', the limit is zero, and the approximation is accurate. The professor then generalizes the conditions under which the approximation is valid, relating it to the concept of higher-order infinitesimals.
🏁 Conclusion: Justifying the Intuitive Approach to Arc Length
The final paragraph concludes the lecture by summarizing the complex process of justifying the intuitive approach to approximating arc length with straight line segments. The professor acknowledges the difficulty of proving that all errors are eliminated in the limit and compares it to the challenges faced in differential calculus with the 0/0 indeterminate form. Ultimately, the lecture establishes that under certain conditions, the intuitive approach aligns with the rigorous mathematical definition of arc length.
Mindmap
Keywords
💡Arc Length
💡Axiom
💡Rectifiable Curve
💡Mean Value Theorem (MVT)
💡Derivative
💡Definite Integral
💡Continuous Function
💡Higher-Order Infinitesimal
💡Squeeze Theorem
💡Intuitive Approach
💡Differentiable
Highlights
The lecture introduces the concept of 'One-dimensional Area', which is arc length, and its complexity compared to area and volume.
The fundamental axioms for arc length are presented, including the measurability of straight line segments and the additive property of arc lengths.
A key difference between arc length and other dimensions is highlighted, where containment of regions does not guarantee lesser perimeter.
The intuitive approach to measuring arc length using a string is discussed, as well as the need for a more analytical method.
The first analytical approach to arc length is explored, which involves approximating arc length with straight line segments.
The limitations of the first approach are demonstrated, showing that it does not align with the intuitive understanding of arc length.
A second analytical approach is introduced, using the cord between endpoints of an arc segment as a better approximation for arc length.
The existence of the limit for arc length approximation is discussed, with the assumption of dealing with rectifiable curves.
The Mean Value Theorem is applied to relate the slope of the cord to the derivative of the curve at a specific point.
The first fundamental theorem of integral calculus is used to express arc length in terms of a definite integral.
The challenge of ensuring the computed limit agrees with the intuitive definition of arc length is addressed.
The concept of infinitesimals and their role in approximating arc length is explained, drawing parallels to differential calculus.
A generalization is made regarding the conditions under which the limit of an approximation equals the function being approximated.
The importance of higher order infinitesimals in ensuring that the error in approximation is negligible as 'delta x' approaches 0.
A plausibility argument is presented to justify the intuitive approach of approximating arc length by straight line segments.
The sensitivity of the 'infinity times 0' form in integral calculus is compared to the '0/0' form in differential calculus.
The conclusion that the analytical approach can validate the intuitive method of approximating arc length concludes the lecture.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: