Math Antics - Volume
TLDRIn this Math Antics lesson, Rob introduces the concept of volume, a fundamental quantity in geometry that measures the 3D space an object occupies. He explains that volume is calculated using cubic units, such as cubic centimeters, and contrasts it with surface area, a 2D quantity. Rob then demonstrates how to calculate the volume of various 3D shapes, including prisms and cylinders, by multiplying the area of the base shape by the extension length. He also covers more complex shapes like spheres and cones, providing formulas for their volumes. The lesson aims to clarify terminology and encourage practice to solidify understanding of this essential geometric principle.
Takeaways
- 📏 Volume is a 3D quantity that measures the space an object occupies.
- 📐 Volume is measured in cubic units, such as cubic centimeters or cubic meters.
- ⬇️ Volume can be calculated by extending 2D shapes along a third dimension.
- 🟦 A rectangular prism's volume is found by multiplying the area of its base by its height.
- 🔺 A triangular prism's volume is calculated by finding the area of the triangle base and multiplying by the prism's height.
- ⚪ A cylinder's volume is found by calculating the area of the circular base and multiplying by its height.
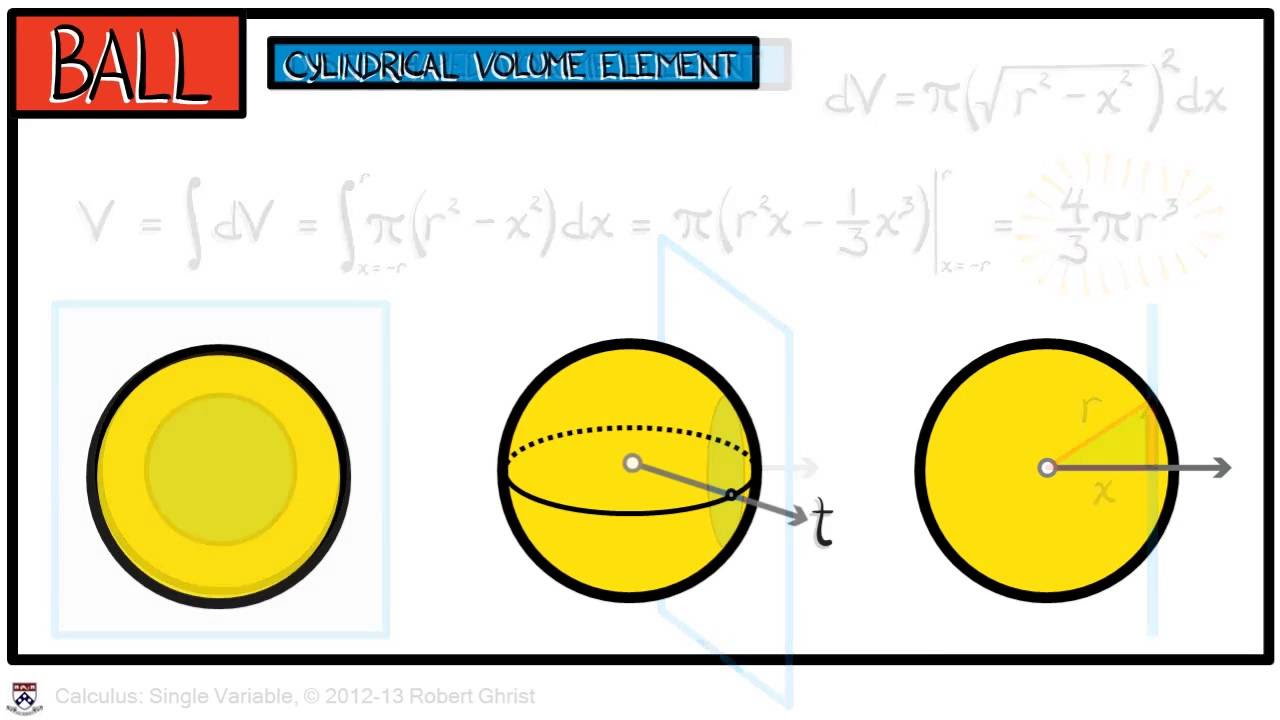
- 🔢 Volume formulas: Sphere - V = 4/3 * π * r^3, Cone - V = 1/3 * π * r^2 * h.
- 🔄 Some 3D shapes are formed by rotating 2D shapes around an axis, like spheres and cones.
- 📏 Surface area is a 2D quantity measuring the outer boundary of a 3D object.
- 🔍 Understanding volume and surface area is crucial for differentiating between the space an object occupies and its external boundary.
Q & A
What is the definition of volume in geometry?
-Volume is a quantity that all 3-Dimensional objects have, which tells us how much 3-Dimensional space an object occupies.
What units are commonly used to measure volume?
-Common units for measuring volume include cubic centimeters, cubic inches, cubic meters, and cubic miles.
How is volume related to the concept of length in 1-Dimensional objects?
-Volume is an extension of the concept of length. Just as length is a 1-Dimensional quantity, volume is a 3-Dimensional quantity that measures the space an object occupies.
How does one calculate the volume of a cube?
-The volume of a cube is calculated by multiplying the length of one side by itself twice (since a cube has equal sides), resulting in a cubic unit, such as one cubic centimeter if each side is one centimeter long.
What is the difference between area and volume?
-Area is a 2-Dimensional quantity that measures the amount of space within a 2-D surface, while volume is a 3-Dimensional quantity that measures the amount of space an object occupies.
How is the volume of a rectangular prism calculated?
-The volume of a rectangular prism is calculated by multiplying the area of the base (a rectangle) by the length of the prism along the third dimension.
What is the formula for calculating the volume of a triangular prism?
-The volume of a triangular prism is calculated by multiplying the area of the base triangle (which is one-half times the base times the height) by the length of the prism along the third dimension.
How do you find the volume of a cylinder?
-The volume of a cylinder is found by multiplying the area of the base circle (pi times the radius squared) by the height of the cylinder.
What is the difference between surface area and volume of a 3D object?
-Surface area is the 2-Dimensional outer boundary of a 3-Dimensional shape, which is the total area of the object's outer surface or shell. Volume, on the other hand, is the 3-Dimensional space that the object occupies.
What are the formulas for calculating the volume of a sphere and a cone?
-The volume of a sphere is calculated using the formula \( \frac{4}{3} \pi r^3 \), and the volume of a cone is calculated using the formula \( \frac{1}{3} \pi r^2 h \), where \( r \) is the radius and \( h \) is the height.
Outlines
📏 Introduction to Volume and Its Measurement
This paragraph introduces the concept of volume, a fundamental quantity in geometry that pertains to the amount of three-dimensional space an object occupies. Rob, the host, begins by explaining the progression from one-dimensional length to two-dimensional area, and finally to three-dimensional volume. He uses a line segment to illustrate length, a square to represent area, and a cube as an example of volume. The importance of cubic units, such as cubic centimeters, is emphasized, and the relationship between square units and cubic units is clarified. The paragraph also touches on the approximation of volume for complex shapes like spheres using smaller cubes, and the distinction between volume and surface area is highlighted, with surface area being the outer boundary of a 3D shape and volume being the space inside.
📐 Calculating Volumes of Simple Geometric Shapes
This paragraph delves into the process of calculating the volume of various simple geometric shapes, starting with a rectangular prism. The base area of the shape is determined by multiplying its length by its width, and then this area is multiplied by the height (or the distance of extension in the third dimension) to find the volume. The same principle is applied to a triangular prism, with the base area being half the product of the base and height of the triangle. The paragraph also covers the volume of a cylinder, which is calculated by multiplying the area of the circular base (pi times the radius squared) by the height of the cylinder. The importance of understanding the base of the shape and the extension length is emphasized, and the paragraph concludes with a reminder that this method can be applied to any 2D shape extended into the third dimension.
🎯 Advanced Volume Calculations: Spheres and Cones
The final paragraph of the script introduces the volume calculations for more complex shapes that are formed by rotation, such as spheres and cones. The formula for the volume of a sphere is presented as four-thirds times pi times the radius cubed, and an example calculation is provided using a sphere with a 2-centimeter radius. For cones, the volume is calculated as one-third times the height times pi times the radius squared, and an example with a cone having a 3-foot radius and a 9-foot height is given. The paragraph concludes with a summary of the key points covered in the video, encouraging viewers to practice volume calculations with various exercises and reminding them of the importance of applying their knowledge to solve problems.
Mindmap
Keywords
💡Volume
💡1-Dimensional
💡2-Dimensional
💡3-Dimensional
💡Cubic Units
💡Surface Area
💡Rectangular Prism
💡Triangular Prism
💡Cylinder
💡Sphere
💡Cone
Highlights
Volume is a 3D quantity that measures how much space an object occupies.
1-Dimensional objects are measured by their length, commonly in centimeters.
2-Dimensional objects, like squares, are measured by area in square units.
Volume is calculated by extending a 2D shape in a third dimension.
The volume of a cube is one cubic centimeter, derived from extending a square centimeter.
Cubic units are used to measure volume, such as cubic centimeters, inches, or meters.
Surface area and volume are distinct; surface area is the outer boundary of a 3D shape.
3D objects can be formed by extending 2D shapes, creating shapes like prisms and cylinders.
The volume of a 3D shape is found by multiplying the area of its base by the extension length.
Rectangular prisms, triangular prisms, and cylinders are examples of 3D shapes formed by extension.
A cylinder's volume is calculated by multiplying the area of its circular base by its height.
Different terminology may be used to describe dimensions, but the mathematical concepts remain the same.
Volume formulas for shapes formed by rotation, like spheres and cones, are more complex and often memorized.
The volume of a sphere is calculated using the formula 4/3 * pi * radius^3.
The volume of a cone is found with the formula 1/3 * height * pi * radius^2.
Practice is essential to apply the knowledge of volume calculations to various 3D shapes.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: