VOLUME OF SOLID FIGURES | GRADE 6

Sheena Doria
23 May 202110:06
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, students are introduced to the concept of volume for various three-dimensional shapes. The lesson begins with a rectangular prism, explaining how to calculate its volume by multiplying length, width, and height. It then compares the prism to a pyramid, demonstrating that a pyramid's volume is one-third that of a prism with equal base and height. The video proceeds to explain the volume calculations for a cube, a cylinder, and a cone, emphasizing the formulas and their geometric relationships. Finally, the volume of a sphere is derived using the formula \( \frac{4}{3}\pi r^3 \). Throughout the lesson, the importance of understanding cubic units and the volume formulas for different shapes is highlighted, providing a comprehensive guide to volume calculations.

Takeaways
  • 🔢 Volume is the amount of space inside a solid figure, measured in cubic units.
  • 📏 The volume of a rectangular prism can be found by multiplying its length, width, and height.
  • 🔲 A cubic unit is a cube whose sides measure one unit, and its volume is one cubic unit.
  • 📦 To find the volume of a rectangular prism, multiply its length, width, and height (V = l × w × h).
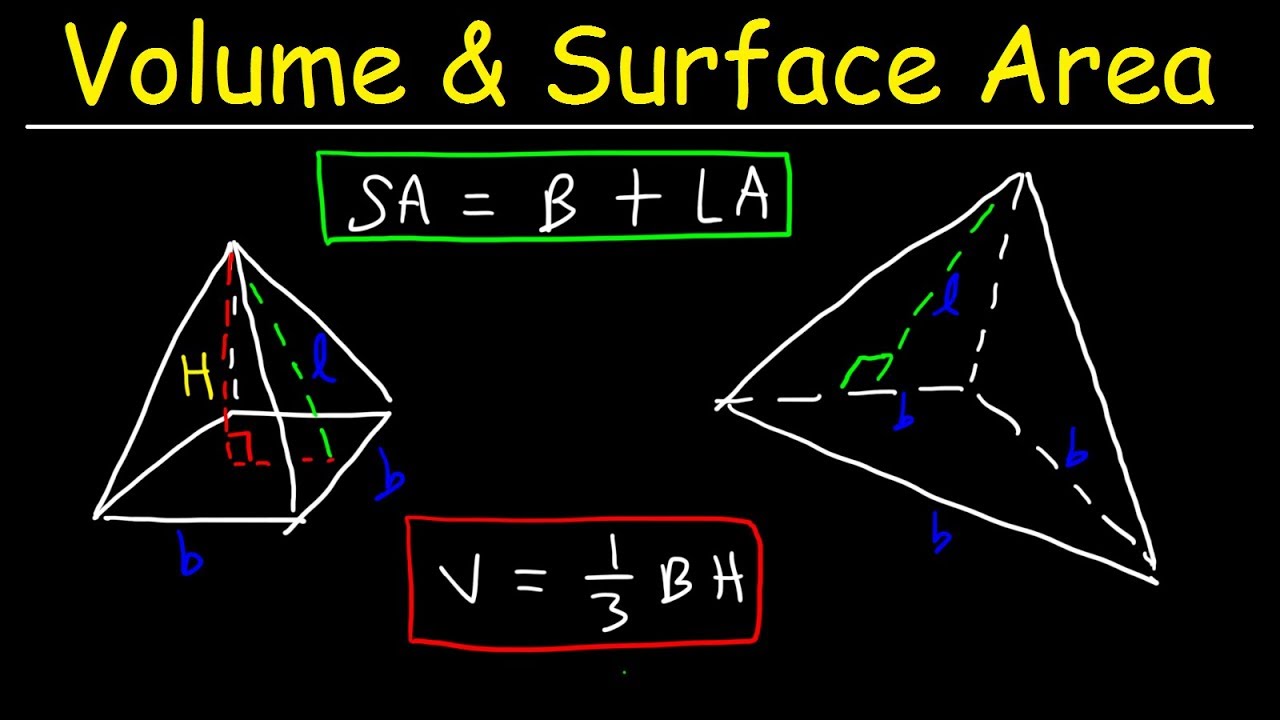
  • 🔺 The volume of a pyramid is one-third the volume of a rectangular prism with the same base and height (V = 1/3 × l × w × h).
  • 🧊 The volume of a cube is found by multiplying the side length by itself three times (V = s³).
  • 🗜️ The volume of a cylinder is found using the formula V = πr²h, where r is the radius and h is the height.
  • 🍦 The volume of a cone is one-third the volume of a cylinder with the same base and height (V = 1/3 × πr²h).
  • ⚪ The volume of a sphere is calculated using the formula V = 4/3 × πr³, where r is the radius.
  • 📚 Understanding the volume of different shapes helps in solving real-life problems involving space and capacity.
Q & A

  • What is the definition of volume as explained in the script?

    -Volume is the amount of space inside a solid figure or three-dimensional figures, measured in cubic units, such as cubic centimeters or cubic meters.

  • How is the volume of a rectangular prism calculated?

    -The volume of a rectangular prism is calculated by multiplying its length, width, and height (V = lwh), or by multiplying the area of the base by the height (V = Bh).

  • What is the volume of the tank in the form of a rectangular prism with dimensions 4 cm in height, 2 cm in length, and 2 cm in width?

    -The volume of the tank is 16 cubic centimeters, calculated by multiplying 4 cm (height) by 2 cm (length) by 2 cm (width).

  • How does the volume of a pyramid compare to the volume of a rectangular prism with the same base and height?

    -The volume of a pyramid is one-third of the volume of a rectangular prism with the same base and height.

  • What is the formula for calculating the volume of a pyramid?

    -The formula for the volume of a pyramid is one-third times the length times the width times the height, or (V = 1/3 * l * w * h).

  • How is the volume of a cube calculated?

    -The volume of a cube is calculated by multiplying the length of one side by itself twice (V = s^3), since all sides of a cube are equal.

  • What is the formula for calculating the volume of a cylinder?

    -The volume of a cylinder is calculated using the formula V = π * r^2 * h, where r is the radius and h is the height.

  • What is the volume of the cylinder with a radius of 4 meters and a height of 8 meters?

    -The volume of the cylinder is 401.92 cubic meters, calculated using the formula π * r^2 * h with π approximated to 3.14.

  • How does the volume of a cone compare to the volume of a cylinder with the same base and height?

    -The volume of a cone is one-third of the volume of a cylinder with the same base and height.

  • What is the formula for calculating the volume of a cone?

    -The formula for the volume of a cone is one-third times π times the radius squared times the height, or (V = 1/3 * π * r^2 * h).

  • How is the volume of a sphere calculated?

    -The volume of a sphere is calculated using the formula V = (4/3) * π * r^3.

  • What is the volume of the sphere with a radius of 3 centimeters?

    -The volume of the sphere is 113.04 cubic centimeters, calculated using the formula (4/3) * π * r^3 with π approximated to 3.14.

Outlines
00:00
📚 Introduction to Volume Calculations

This paragraph introduces the lesson on calculating the volume of various solid figures, including a rectangular prism, pyramid, cylinder, cone, and sphere. The teacher begins with a tank shaped like a rectangular prism, measuring 4 cm in height, 2 cm in length, and 2 cm in width. The concept of volume is explained as the amount of space inside a three-dimensional figure, measured in cubic units. The teacher demonstrates how to calculate the volume of the prism by counting the number of 1 cm³ cubic units that fit inside, resulting in 16 cubic centimeters. The formula for the volume of a prism is presented as length times width times height (lwh), or the area of the base times the height (bh). The lesson then moves on to calculate the volume of a pyramid, which is one-third of the volume of a prism with the same base and height, using the formula (lwh)/3.

05:04
📏 Volume Calculations for Cubes, Cylinders, and Cones

In this paragraph, the teacher continues the lesson by calculating the volume of a cube with sides measuring 2 meters, using the formula side times side times side (s³), resulting in 8 cubic meters. Next, the volume of a cylinder with a radius of 4 meters and a height of 8 meters is calculated using the formula πr²h, where π is approximated as 3.14. The calculation yields a volume of 401.92 cubic meters. The teacher then explains the volume of a cone, which is one-third of the volume of a cylinder with the same base and height, using the formula (πr²h)/3. An example cone with a height of 6 decimeters and a radius of 2 decimeters is used to demonstrate the calculation, resulting in a volume of 25.12 cubic decimeters.

🌐 Calculating the Volume of a Sphere

The final paragraph focuses on calculating the volume of a sphere with a radius of 3 centimeters. The formula for the volume of a sphere is given as (4/3)πr³. Using the value of π as 3.14, the teacher demonstrates the calculation: 4 times 3.14 times the cube of the radius (3 cm)³, which simplifies to 4 * 3.14 * 27 cubic centimeters, and then divided by 3, resulting in a volume of 113.04 cubic centimeters. The paragraph concludes with a summary of the concepts learned in the lesson, highlighting the importance of understanding volume calculations for different geometric shapes.

Mindmap
Keywords
💡Volume
Volume refers to the amount of space that a solid figure occupies. In the context of the video, it is a fundamental concept that is measured in cubic units, such as cubic centimeters or cubic meters. The script explains that volume is distinct from area, which is measured in square units. The video's theme revolves around calculating the volume of various three-dimensional shapes, such as prisms, pyramids, cylinders, cones, and spheres, making volume a central concept.
💡Rectangular Prism
A rectangular prism is a three-dimensional shape with six rectangular faces. In the script, the teacher uses a tank in the shape of a rectangular prism as an example to illustrate the concept of volume. The dimensions given are a height of four centimeters, a length of two centimeters, and a width of two centimeters. The volume of this prism is calculated by multiplying these dimensions, demonstrating how the concept of volume applies to a real-world object.
💡Cubic Units
Cubic units are the standard units used to measure volume. The script mentions cubic units to explain that volume is measured in three-dimensional space. An example given is a cube with sides measuring one unit, resulting in a volume of one cubic unit. This concept is essential for understanding how to calculate the volume of different shapes, as it is the basis for the formulae used in the video.
💡Pyramid
A pyramid is a polyhedron with a polygonal base and triangular faces that meet at a single point called the apex. In the video script, the pyramid's volume is discussed, and it is calculated as one-third of the volume of a rectangular prism with the same base and height. This highlights the relationship between the volume of a pyramid and the volume of a prism, which is a key point in the lesson.
💡Cube
A cube is a special type of rectangular prism where all sides are of equal length. The script provides an example of a cube with sides measuring two meters and explains that the volume of a cube is calculated by multiplying the length of one side by itself twice (s^3). This concept is used to demonstrate the simplicity of calculating volume when all sides are equal.
💡Cylinder
A cylinder is a three-dimensional shape with two parallel and congruent circular bases connected by a curved surface. The script explains the formula for the volume of a cylinder as pi times the square of the radius times the height (πr^2h). This formula is applied to an example with a radius of four meters and a height of eight meters, showing how to calculate the volume of a cylindrical object.
💡Cone
A cone is a geometric shape that tapers smoothly from a base to a point called the apex. The script teaches that the volume of a cone is one-third of the volume of a cylinder with the same base and height. The formula used is one-third times pi times the square of the radius times the height (1/3πr^2h). An example with a height of six decimeters and a radius of two decimeters is provided to illustrate the calculation.
💡Sphere
A sphere is a perfectly symmetrical three-dimensional shape where all points on the surface are equidistant from the center. The script introduces the formula for the volume of a sphere as four-thirds times pi times the cube of the radius (4/3πr^3). An example with a radius of three centimeters is used to demonstrate the calculation of the volume of a spherical object.
💡Pi (π)
Pi, denoted as π, is a mathematical constant representing the ratio of a circle's circumference to its diameter. In the script, π is used in the formulas for calculating the volumes of cylinders and spheres. The value of π is approximately 3.14, and it is essential for understanding how to apply these formulas correctly in the context of the video.
💡Base Area
Base area is the area of the base of a three-dimensional shape, such as a prism or a pyramid. In the script, the concept of base area is introduced when explaining the volume of a prism, where the base area is multiplied by the height to find the volume. This concept is crucial for understanding how the dimensions of the base contribute to the overall volume of a shape.
Highlights

Introduction to the lesson on calculating the volume of various solid figures.

Explanation of a tank in the shape of a rectangular prism with dimensions provided.

Recap on the concept of volume as the amount of space inside a solid figure.

Clarification that volume is measured in cubic units, not square units like area.

Illustration of forming a rectangular prism with cubic units and calculating its volume.

Formula for the volume of a rectangular prism: length times width times height.

Alternative method for calculating volume: area of the base times height.

Demonstration of calculating the volume of a pyramid with a given height, length, and width.

Formula for the volume of a pyramid: one-third times length times width times height.

Calculation of the volume of a cube with sides measuring 2 meters.

Introduction of the formula for the volume of a cylinder: pi times radius squared times height.

Calculation of the volume of a cylinder with a radius of 4 meters and a height of 8 meters.

Introduction of the formula for the volume of a cone: one-third times pi times radius squared times height.

Calculation of the volume of a cone with a height of six decimeters and a radius of two decimeters.

Introduction of the formula for the volume of a sphere: four-thirds times pi times radius cubed.

Calculation of the volume of a sphere with a radius of 3 centimeters.

Summary of the lesson on volume calculations for various solid figures.

Transcripts

Browse More Related Video

Volume

Math Antics - Volume

Surface Area of a Pyramid & Volume of Square Pyramids & Triangular Pyramids

Volume with cross sections: intro | Applications of integration | AP Calculus AB | Khan Academy

Optimisation Grade 12: Maximum Volume Cone

AP CALCULUS AB 2022 Exam Full Solution FRQ#4d

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Volume CalculationMath Education3D ShapesRectangular PrismPyramid VolumeCylinder FormulaCone VolumeSphere VolumeGeometry LessonPi ApplicationCube Dimensions