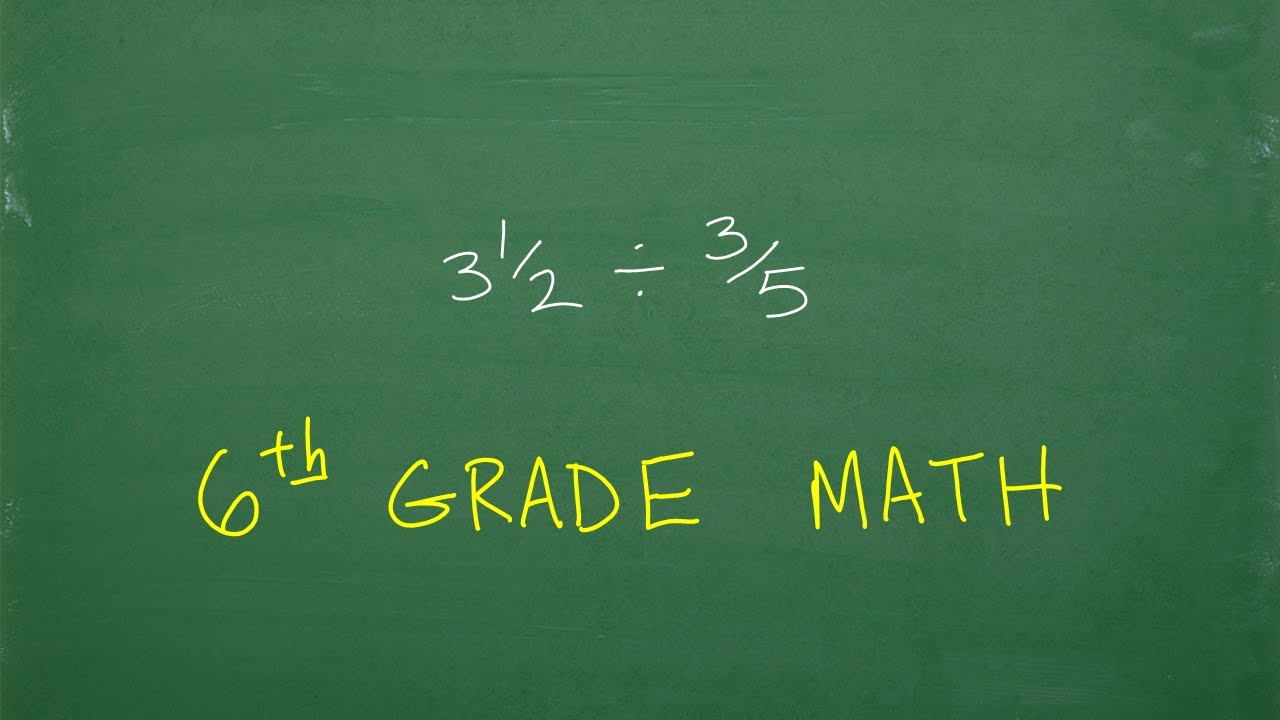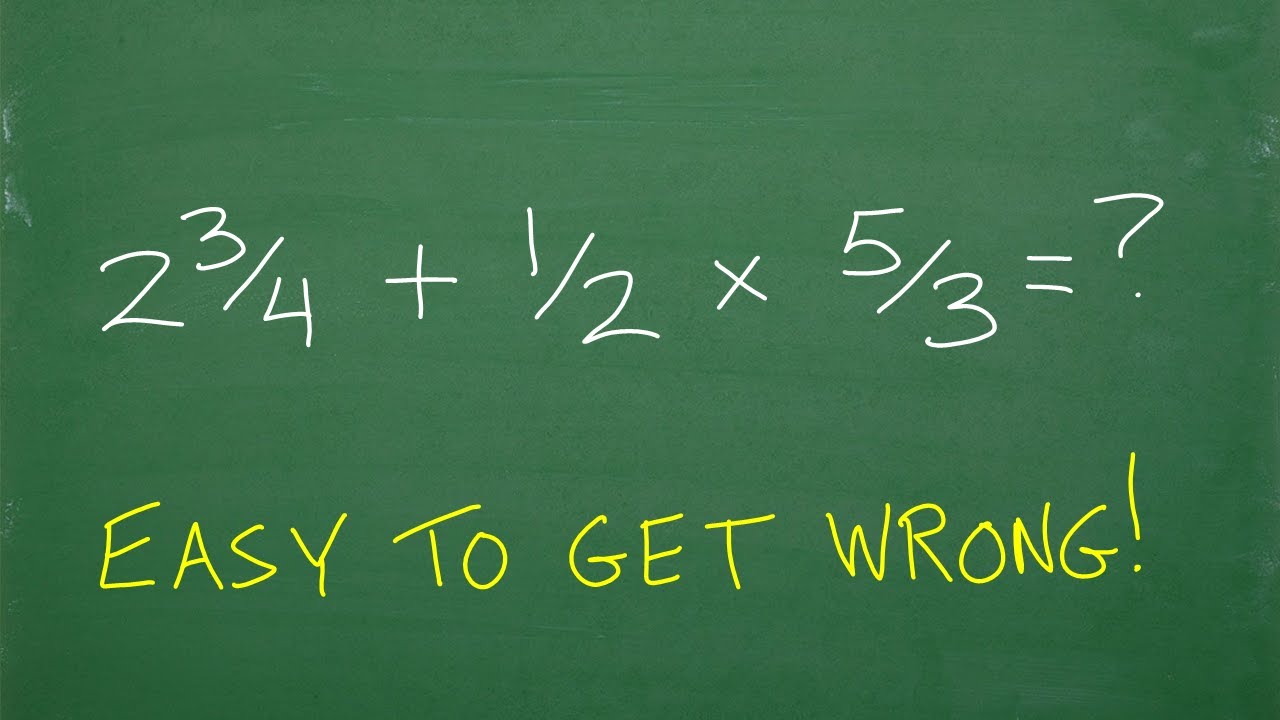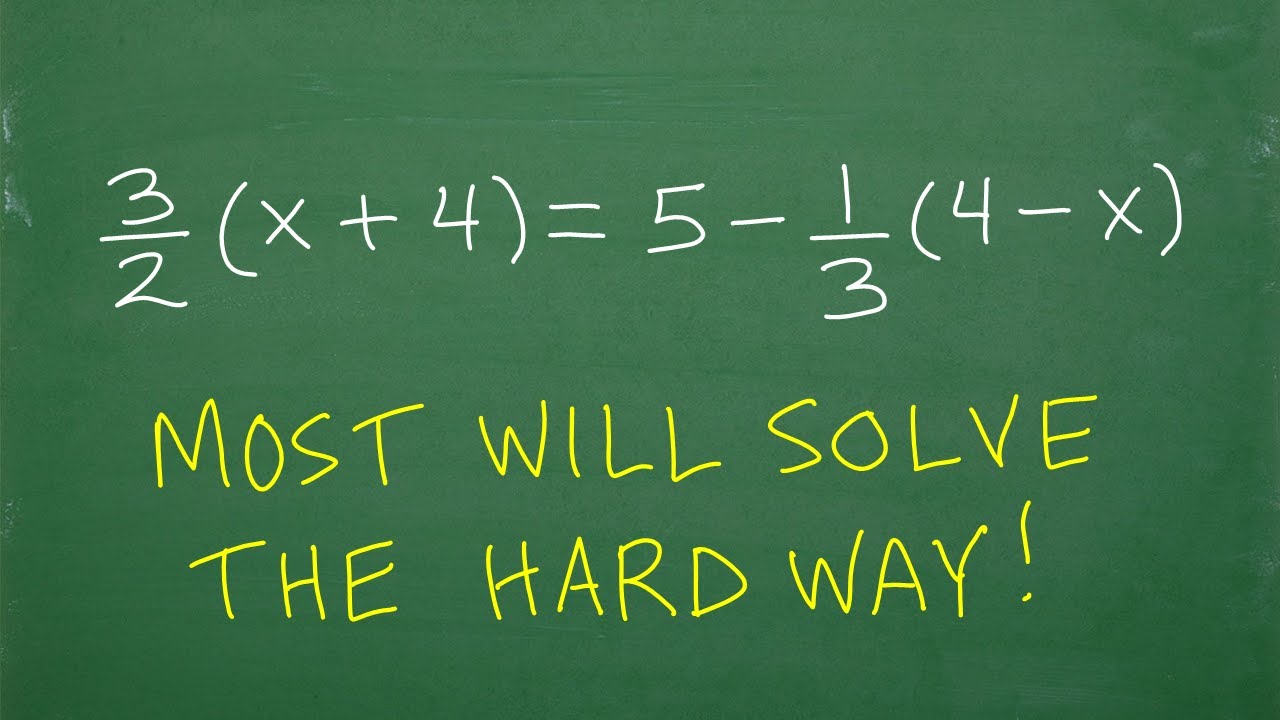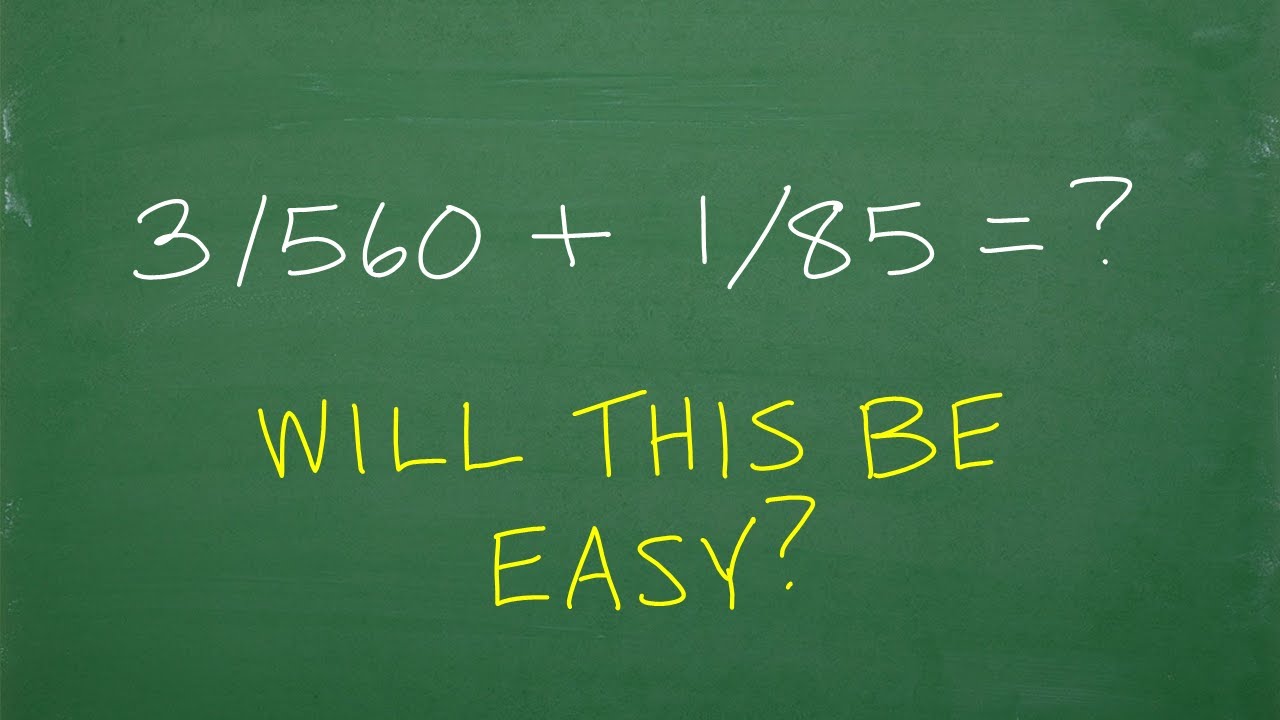How to Multiply Fractions – 6th Grade Math
TLDRIn this instructional video, John, the founder of tcmath Academy and an experienced math teacher, simplifies the process of multiplying fractions, a crucial skill for students from sixth grade and beyond. He emphasizes the importance of mastering fractions as they are fundamental across all levels of mathematics. John walks viewers through the steps of multiplying fractions, including converting mixed numbers to improper fractions and simplifying results. He also highlights the ease of multiplication compared to addition and subtraction of fractions, which often require finding a common denominator. The video is designed to boost students' confidence and provide clear guidance on tackling fractions in their math studies.
Takeaways
- 📚 Fractions are a fundamental topic in mathematics taught from elementary school through higher levels.
- 🔢 Multiplying fractions is considered the easiest operation among addition, subtraction, multiplication, and division of fractions.
- 👨🏫 John, the founder of tcmath Academy and a middle/high school math teacher, provides instruction and resources for struggling math students.
- 🔗 John offers a math help program with comprehensive math instruction for middle school, high school, and college students, as well as test preparation.
- 📈 To multiply fractions, you multiply the numerators together and the denominators together, and then simplify the result if possible.
- 📉 Cross-canceling is a technique used during multiplication to simplify fractions by eliminating common factors between the numerator and the denominator.
- 📉 Mixed numbers, which are whole numbers combined with fractions, must be converted into improper fractions before multiplication.
- 📉 Converting improper fractions to mixed numbers involves dividing the numerator by the denominator and expressing the remainder as a fraction.
- ⚠️ It's advised not to convert final answers from improper fractions to mixed numbers unless specifically instructed to do so, to avoid errors and save time.
- 📝 When multiplying fractions, it's crucial to ensure the answer is fully simplified to avoid losing points in assessments.
- 📚 Additional resources such as math notes and courses are available for those who need extra help with fractions and other math topics.
Q & A
What is the primary topic of the video?
-The primary topic of the video is how to multiply fractions, which is a fundamental concept in mathematics, especially for sixth grade level and above.
Who is the speaker in the video?
-The speaker in the video is John, the founder of tcmath Academy and a middle and high school math teacher.
What is the order of difficulty when dealing with fractions?
-The order of difficulty when dealing with fractions is as follows: multiplying fractions is the easiest, followed by dividing fractions, then adding and subtracting fractions.
Why is it important to understand fractions in mathematics?
-Understanding fractions is important because they are everywhere in mathematics at all levels, and being able to work with fractions is essential for success in various mathematical topics and applications.
How does one multiply two fractions?
-To multiply two fractions, you multiply the respective numerators and then multiply the respective denominators. The result is the new fraction with the product of the numerators as the new numerator and the product of the denominators as the new denominator.
What is the concept of cross canceling in fraction multiplication?
-Cross canceling is a technique used to simplify the result of a fraction multiplication by finding common factors in the numerator and denominator, which can then be canceled out, leaving the simplest form of the fraction.
How can one convert a mixed number to an improper fraction?
-To convert a mixed number to an improper fraction, you multiply the whole number part of the mixed number by the denominator of the fraction and add the fraction part to the result. The final result is the improper fraction, where the numerator is the product of the whole number and the fraction part, and the denominator is the original denominator.
Why should one avoid converting a fully simplified improper fraction into a mixed number unless instructed to do so?
-One should avoid converting a fully simplified improper fraction into a mixed number unless instructed to do so because it takes additional time and can lead to errors. The final answer should always be fully simplified, and in some cases, it is not necessary to express the answer in mixed number form.
What is the significance of fully simplifying a fraction?
-Fully simplifying a fraction is important because it ensures that the answer is in its most reduced form, which is necessary for accuracy and to avoid unnecessary complications in mathematical problems.
How can one add and subtract fractions?
-To add and subtract fractions, one must find a common denominator and then add or subtract the numerators while keeping the denominators the same. This process can be challenging, especially when dealing with larger numbers, but it is a crucial skill for understanding more advanced mathematical concepts.
What are some of the common mistakes made when dealing with fraction multiplication and division?
-Common mistakes when dealing with fraction multiplication and division include not fully simplifying the result, not using cross canceling to simplify the fraction, and not converting mixed numbers to improper fractions when necessary. These mistakes can lead to incorrect answers and can be avoided by following proper mathematical procedures and techniques.
Outlines
📚 Introduction to Multiplying Fractions
In this paragraph, John introduces the topic of multiplying fractions, emphasizing its importance in middle school and beyond. He categorizes the difficulty levels of various fraction operations and reassures students about the relative ease of multiplication. John shares his personal dislike for fractions during his school years and highlights the necessity of understanding fractions at all levels of mathematics. He promises a review of multiplying fractions and introduces himself as the founder of TCMath Academy, offering resources for further math help.
🔄 Cross-Canceling Fractions
John explains how to cross-cancel fractions to simplify multiplication. He demonstrates this technique using the example of multiplying one-half by four-thirds. By breaking down numbers into factors and canceling like factors in the numerator and denominator, he shows how to simplify fractions during multiplication. He emphasizes the importance of fully simplifying fractions and provides a detailed step-by-step process for cross-canceling.
🔢 Working with Mixed Numbers
This paragraph focuses on multiplying mixed numbers. John explains how to convert mixed numbers to improper fractions before multiplying. He demonstrates this process with examples, showing how to multiply the respective numerators and denominators and then simplifying the result. He advises students to avoid converting back to mixed numbers unless required by the teacher, to save time and avoid mistakes. He emphasizes the importance of ensuring all fractions are fully simplified.
💡 Additional Tips and Conclusion
John concludes the lesson by reviewing key points about multiplying fractions, including the importance of starting with multiplication before moving to division, addition, and subtraction. He reassures students that multiplying and dividing fractions are straightforward and highlights the challenges students often face with addition and subtraction due to the need to find the least common denominator (LCD). He suggests checking out his videos for tips on these operations and recommends specific courses for more formal instruction on fractions. John ends with well wishes for students' success in mathematics.
Mindmap
Keywords
💡fractions
💡multiplying fractions
💡simplifying fractions
💡cross-canceling
💡mixed numbers
💡improper fractions
💡LCD (Least Common Denominator)
💡mathematical operations
💡math instruction
💡mathematical concepts
Highlights
Multiplication of fractions is the easiest operation to master, followed by division, and then addition and subtraction.
John, the founder of tcmath Academy, emphasizes the importance of great math instruction and offers his math help program for middle, high school, and college students.
To multiply fractions, multiply the numerators and denominators separately, ensuring the result is fully simplified for accuracy.
Cross canceling is a technique used to simplify the result of a fraction multiplication by canceling common factors.
Mixed numbers can be converted into improper fractions, and vice versa, which is essential for multiplication and other operations involving fractions.
When multiplying mixed numbers, it's important to convert them into improper fractions first before multiplying the numerators and denominators.
To avoid losing points on quizzes or tests, it's advised not to convert fully simplified answers into mixed numbers unless explicitly instructed to do so.
Multiplication of fractions is a fundamental skill that should be learned before attempting more complex operations like addition and subtraction.
John provides resources for various levels of mathematics, including pre-algebra and math foundations courses, to help students excel in their studies.
The video also mentions the importance of understanding and applying the technique for adding and subtracting fractions, which can be found in John's additional videos.
John's approach to teaching math is to provide clear, understandable, and comprehensive instruction, aiming to help students overcome struggles in mathematics.
The video encourages viewers to engage by asking them to provide the answer to a multiplication problem involving fractions and to like and subscribe to the channel for more content.
John's message is to not give up on mathematics and to seek out great math instruction to be successful, as he has been doing for decades as a math teacher.
The video is part of a series that includes multiple videos on fractions, with over a million views, indicating its popularity and effectiveness.
The transcript also touches on the importance of fully simplifying answers in math, which is a common point of contention and confusion among students.
John's method of teaching involves not only explaining the steps but also showing the audience how to apply these methods in practice, such as through cross canceling.
The video concludes with a positive note, encouraging viewers to do well in their mathematics studies and to seek out additional resources if needed.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: